题意:
给一些无序的数字,求解一个矩阵,使得矩阵的每一个元素都是行和列标志数的gcd,输出行标志数。
首先对数字进行排序。复杂度n*log(n^2)。
这题的证明有官方的英文题解==在这直接贴英文题解...
这题我事后自己反思了一下,其实思路并不难,而且一开始自己思考的方向也对。
问题出在两方面:
1.对平衡树等数据结构的应用还是缺乏理解的。遇到问题不知道可以用这些方法来解决。
2.思考缺乏理性和条理。没有按部就班得思考。
Let the answer be a1 ≤ a2 ≤ ... ≤ an. We will use the fact that gcd(ai, aj) ≤ amin(i, j).
It is true that gcd(an, an) = an ≥ ai ≥ gcd(ai, aj) for every 1 ≤ i, j ≤ n. That means that an is equal to maximum element in the table. Let set an to maximal element in the table and delete it from table elements set. We've deleted gcd(an, an), so the set now contains all gcd(ai, aj), for every 1 ≤ i, j ≤ n and 1 ≤ min(i, j) ≤ n - 1.
By the last two inequalities gcd(ai, aj) ≤ amin(i, j) ≤ an - 1 = gcd(an - 1, an - 1). As soon as set contains gcd(an - 1, an - 1), the maximum element in current element set is equal to an - 1. As far as we already know an, let's delete the gcd(an - 1, an - 1), gcd(an - 1, an), gcd(an, an - 1)from the element set. Now set contains all the gcd(ai, aj), for every 1 ≤ i, j ≤ n and1 ≤ min(i, j) ≤ n - 2.
We're repeating that operation for every k from n - 2 to 1, setting ak to maximum element in the set and deleting the gcd(ak, ak), gcd(ai, ak), gcd(ak, ai) for every k < i ≤ n from the set.
One could prove correctness of this algorithm by mathematical induction. For performing deleting and getting maximum element operations one could use multiset or map structure, so solution has complexity 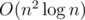 .
.
来源:http://codeforces.com/blog/entry/20692
这里学了一下multiset的各种应用....
#include<stdio.h> #include<queue> #include<string.h> #include<set> #include<algorithm> using namespace std; int n; int ttmp[600]; multiset<int>s; int gcd(int a,int b) { return b==0?a:gcd(b,a%b); } int main() { int n,tmp; scanf("%d",&n); for(int i=1;i<=n*n;i++) { scanf("%d",&tmp); s.insert(tmp); } int num=1; ttmp[num]=*s.rbegin(); s.erase(s.find(*s.rbegin())); while(num<n) { num++; ttmp[num]=*s.rbegin(); s.erase(s.find(*s.rbegin())); for(int i=num-1;i>=1;i--) { s.erase(s.find(gcd(ttmp[i],ttmp[num]))); s.erase(s.find(gcd(ttmp[i],ttmp[num]))); } } for(int i=1;i<=n;i++) { printf("%d ",ttmp[i]); } return 0; }