前言
在前面的博文PCA算法学习_1(OpenCV中PCA实现人脸降维)中已经初步介绍了PCA算法的大概流程及在人脸降维上面的应用。本文就进一步介绍下其理论基础和matlab的实现(也是网上学者的代码)。
开发环境:Matlab2012a
基础
假设X是一个m*n的矩阵,是由样本数据构成的矩阵。其中m表示样本的属性维数,n表示样本的个数。现在要对X进行线性变换变成另一个矩阵Y,使得Y的协方差矩阵为对角矩阵,这样的Y就认为是对原始矩阵X提取主成分后的矩阵,实际过程中只需取Y的前面主要的行即可。
X变换到Y的线性变换公式为:
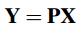
X和Y的协方差计算方法为:

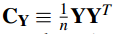
从下面的公式可以看出Cy和Cx的关系为:

因为Cx是对称矩阵,对Cx进行特征值分解就可以将其变换成对角矩阵,见下面的公式推导:

公式中的P和E满足:
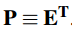
其中D是由Cx的特征向量构成的对角矩阵。P是线性变换矩阵,P的每一行都是Cx矩阵的特征向量,且P是正交矩阵,一般情况下把特征值大的特征向量排在矩阵前面几行。
由此可知,求出P后就可以求出X主成分矩阵了。
另外,还可以求出PCA的白化矩阵,PCA的白化矩阵就是特征向量去相关的矩阵,白化矩阵的协方差阵一般为单位矩阵,在PCA中可以这么求:inv(sqrt(D))*E'。普通的PCA算法可以将输入矩阵X变成主成分矩阵Y,尽管Y的协方差矩阵是个对角矩阵,但不一定是单位矩阵,如果对Y继续使用白化操作,则Y的协方差矩阵就变成了单位矩阵了。
源码
该pca函数接口形式为:
[Y,V,E,D] = pca(X)
其中X为输入数据,X的每一列是一个输入样本。返回值Y是对X进行PCA分析后的投影矩阵。V是与X有关的协方差矩阵特征向量的白化矩阵,E是对应的特征向量(列)构成的矩阵,D是对应的特征值构成的对角矩阵(特征值处于对角线上)。返回值中的白化矩阵,特征向量和特征值都是按照对应特征值大小进行排序后了的。
其matlab源码如下:
function [Y,V,E,D] = pca(X) % do PCA on image patches % % INPUT variables: % X matrix with image patches as columns % % OUTPUT variables: % Y the project matrix of the input data X without whiting % V whitening matrix % E principal component transformation (orthogonal) % D variances of the principal components %去除直流成分 X = X-ones(size(X,1),1)*mean(X); % Calculate the eigenvalues and eigenvectors of the new covariance matrix. covarianceMatrix = X*X'/size(X,2); %求出其协方差矩阵 %E是特征向量构成,它的每一列是特征向量,D是特征值构成的对角矩阵 %这些特征值和特征向量都没有经过排序 [E, D] = eig(covarianceMatrix); % Sort the eigenvalues and recompute matrices % 因为sort函数是升序排列,而需要的是降序排列,所以先取负号,diag(a)是取出a的对角元素构成 % 一个列向量,这里的dummy是降序排列后的向量,order是其排列顺序 [dummy,order] = sort(diag(-D)); E = E(:,order);%将特征向量按照特征值大小进行降序排列,每一列是一个特征向量 Y = E'*X; d = diag(D); %d是一个列向量 %dsqrtinv是列向量,特征值开根号后取倒,仍然是与特征值有关的列向量 %其实就是求开根号后的逆矩阵 dsqrtinv = real(d.^(-0.5)); Dsqrtinv = diag(dsqrtinv(order));%是一个对角矩阵,矩阵中的元素时按降序排列好了的特征值(经过取根号倒后) D = diag(d(order));%D是一个对角矩阵,其对角元素由特征值从大到小构成 V = Dsqrtinv*E';%特征值矩阵乘以特征向量矩阵