题目描述
首先我们简化一下题意:
要找一段区间[L,R],使区间[L,R]内元素最大值减最小值大于等于D。
做法:
首先很容易想到采用二分,分什么呢?
我们二分区间长度为mid
这个时候,检验就成为了我们的目标
最暴力的检验就是枚举左端点,在区间内找最大和最小,有一个max-min>=D
让我们模拟一下:
假如mid=2:
(1) [1,3]
(2) [2,4]
(3) [3 5]
(4) .....
我们震惊的发现:P1886 滑动窗口
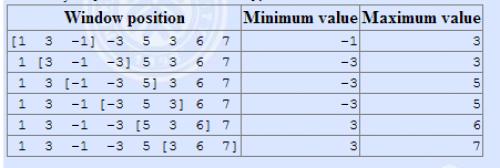
这貌似有点相似
于是正解出现了
正解:
二分区间长度为mid,检验时用单调队列维护区间最大最小值,复杂度nlogn,更多细节见代码:
代码时间到:
#include<bits/stdc++.h> using namespace std; int n,D,l,r; struct WATER{ int x,y; }p[100010]; int ans=2100000000; int q1[100010],q2[100010]; int p1[100010],p2[100010]; int head1=1,tail1=1,head2=1,tail2=1; bool check(int k){ int L=1; q1[1]=p[1].y;p1[1]=p[1].x; q2[1]=p[1].y;p2[1]=p[1].x; head1=1,tail1=1,head2=1,tail2=1; for(int i=2;i<=n;i++){ while((p[i].x-p[L].x)>k) L++; while(p1[head1]<p[L].x&&head1<=tail1) head1++; while(p2[head2]<p[L].x&&head2<=tail2) head2++; while(q1[tail1]<=p[i].y&&head1<=tail1) tail1--; p1[++tail1]=p[i].x;q1[tail1]=p[i].y; while(q2[tail2]>=p[i].y&&head2<=tail2) tail2--; p2[++tail2]=p[i].x;q2[tail2]=p[i].y; if((q1[head1]-q2[head2])>=D) return 1; } return 0; } bool cmp(WATER a,WATER b){ return a.x<b.x; } int main(){ scanf("%d%d",&n,&D); for(int i=1;i<=n;i++) scanf("%d%d",&p[i].x,&p[i].y); l=0,r=1000010; sort(p+1,p+n+1,cmp); while(l<=r){ int mid=(l+r)/2; if(check(mid)){ r=mid-1; ans=min(ans,mid); } else l=mid+1; } if(ans==2100000000) printf("-1"); else printf("%d",ans); return 0; }