滑动窗口的最大值

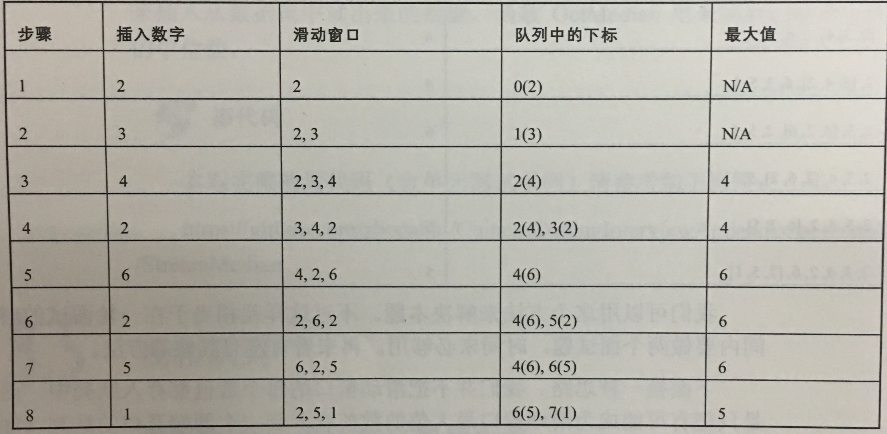
题目：给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

思路：

如果用暴力搜索算法，毫无疑问，时间复杂度为O（nk）。我们可以开辟一个双端队列来存储有可能成为滑动窗口最大值的数的下标，使当前滑动窗口的最大值为队列的第一个元素，每次从数组中取出一个元素与队列中尾端元素进行比较，前者大于后者则移除后者，往队列尾端加入前者，前者小于后者就直接加入队列尾端。

以数组{2,3,4,2,6,2,5,1}为例讲解。数组第一个数是2，存入队列，第二个数是3，3大于2，把2移除，存入3，第三个数是4,4大于3，把3移除，存入4，此时队列的元素为{4}；

第四个数是2，2小于4，当4滑出滑动窗口之后，2有可能成为最大值，把2存入队列尾部，此时队列元素为{4,2}；

第五个数是6，6大于队列中的2和4，因此2和4已经不可能成为滑动窗口中的最大值，从队列中移除2和4；

第六个数是2，2小于6，存入队列，此时队列元素为{6,2}；

第七个元素是5,5与队列的尾端比较，5大于2，移除2，5小于6，把5存入队列尾端，此时队列元素为{6,5}；

最后一个元素是1，1小于5，入队列，但此时6已经不在滑动窗口中了，移除6，队列中元素为{5,1}。

如何判断一个数是否在滑动窗口中呢？

这就是为什么把数字在数组中的下标存到数组而不是把数字存到数组的原因，当一个数字的下标与当前处理的数字的下标之差大于或等于滑动窗口的大小时，这个数字已经从滑动窗口中滑出，可以从队列中移除了。

这种算法的时间复杂度为O(n)。

参考代码：

import java.util.ArrayList;
import java.util.LinkedList;

public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size)
    {
        ArrayList<Integer> result = new ArrayList<Integer>();
        if(num == null || num.length == 0 || size == 0)return  result;
        LinkedList<Integer> queue = new LinkedList<Integer>();
　　　　　//初始化
        for(int i=0;i<size-1;i++){
            while(!queue.isEmpty() && num[i] > num[queue.getLast()]){
                queue.removeLast();
            }
            queue.addLast(i);
        }
        
        for(int i=size-1;i<num.length;i++){
            while(!queue.isEmpty() && num[i] > num[queue.getLast()]){
                queue.removeLast();
            }
            queue.addLast(i);
　　　　　　　//数字是否在滑动窗口中
            if (i-queue.getFirst()+1 > size)
                queue.removeFirst();
            result.add(num[queue.getFirst()]);
        }
        return result;
    }
}