P1113 杂务

既然是工作之间的相互关系，那么一定是有向无环图，所以可以用记忆化来做

状态定义：(f[i])表示从(i)号工作开始完成后续所有工作的安排方法集合，存储能够完成(i)号及其后续所有工作所需的最短时间

状态转移：(f[i] = w[i] + max{f[j_1], f[j_2],...f[j_k],...},)其中(i)是(j_k)的直接准备工作（即DAG上存在(i o j_k)的边）

初始条件：对于没有后续的结点(k)，(f[k] = w[k])

答案：(max{f[i]},i)为所有的无前驱的结点

邻接表存图复杂度：(O(N + E))

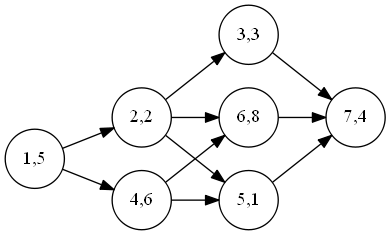
样例的图：

#include<iostream>
#include<cstring>

using namespace std;

const int N = 10010, M = 1000010;

int h[N], e[M], ne[M], idx;
int w[N], in[N], f[N];
int n;

void add(int a, int b){
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

int dfs(int u){
    if(f[u]) return f[u];
    
    f[u] = w[u];
    
    for(int i = h[u]; i != -1; i = ne[i]){
        int j = e[i];
        f[u] = max(f[u], w[u] + dfs(j));
    }
    
    return f[u];
}

int main(){
    memset(h, -1, sizeof h);
    
    cin >> n;
    
    for(int i = 1; i <= n; i ++){
        int num, len;
        cin >> num >> len;
        
        w[num] = len;
        
        int pre;
        while(cin >> pre, pre) add(pre, num), in[num] ++;
    }
    
    int res = 0;
    
    for(int i = 1; i <= n; i ++)
        if(in[i] == 0)
            res = max(res, dfs(i));
            
    cout << res << endl;
    
    return 0;
}