1. Prefix Sum
前缀求和由一个二元操作符和一个输入向量组成,虽然名字叫求和,但操作符不一定是加法。先解释一下,以加法为例:

第一行是输入,第二行是对应的输出。可以看到,Output[1] = Input[0] + Input[1],而Output[length - 1]就是整个输入向量元素之和。
为什么要使用并行计算?假如用串行计算来计算输出向量,那么向量中越靠后的元素需要等待的时间越长。最后一个元素需要等待0 + 1 + 2 + ... + (n - 2) = (n - 1)(n - 2) / 2次加法计算后,才开始计算该元素。在很多情况下是不容许等待这么长时间的。因此需要并行计算。
一个很简单的想法是为输出向量每一个元素分配一个线程,该线程计算对应元素的值。这个方法有两个明显的问题。首先,这样产生的线程的计算负载非常不均衡,T1只运行一次加法,而T[length - 1]需要运行n - 1次加法。整个并行算法的时间由负载最高的线程决定,也就是O(N)。其次,输入向量中,第一个元素会被所有线程读取,第二个被n - 1个线程读取,总共下来,会有O(N * N)次读取。前面也提到过,内存读取是一种比较慢的操作,过多的内存读取会影响算法的性能。
上面的想法也说明一个现象:并行计算非常的简单,只要不考虑计算的性能。
Exclusive 和 Inclusive区别如下图
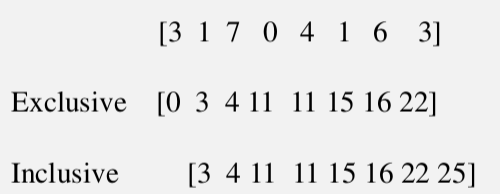
Exclusive 和 Inclusive是可以互相转换的, Exclusive把Inclusive添加0作为首元素,去除最后一个元素得到的新的数组就是Exclusive.
2. Prefix Sum并行算法一
下图是一种改进后的算法:

从队首开始,首先与相邻元素相加,然后与距离2,距离4的元素相加,以此类推。可以证明其正确性。显而易见,此算法需要O(logN)步,和O(NlogN)次的加法操作。
以Exclusive为例构造kernel:
__global__ void work_inefficient_scan_kernel(float *X, float *Y, int InputSize) { _shared__ float XY[BLOCK_SIZE]; int i = blockIdx.x*blockDim.x + threadIdx.x; if (i < InputSize) {XY[threadIdx.x] = X[i];} // the code below performs iterative scan on XY for (unsigned int stride = 1; stride <= threadIdx.x; stride *= 2) { __syncthreads(); float in1 = XY[threadIdx.x-stride]; __syncthreads(); XY[threadIdx.x] += in1; } }
这个kernel的 block_size = InputSize = sharedMemory size, 通过一个threadBlock完成scan,这个情况搜限制于blocksize的大小,一般是1024,所以在数据量不大的时候(即logN不大),这个算法比较快,可以考虑使用。
3. Prefix Sum并行算法二
4.2 CUDA Reduction 一步一步优化里面介绍的思路可以优化Prefix Sum算法.可以分成两个步骤来执行:
1. Parallel Scan - Reduction Phase
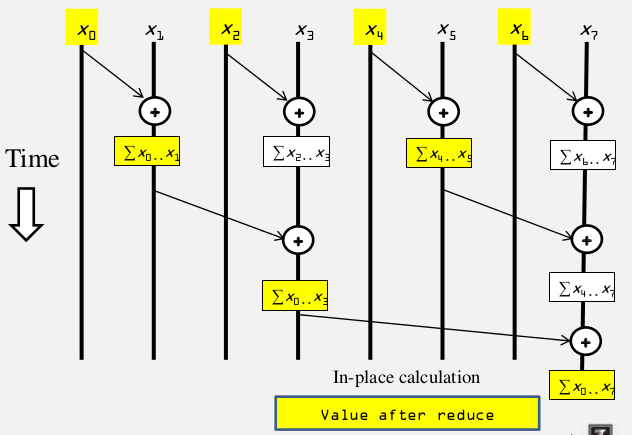
reduction phrase kernel 代码:
for (unsigned int stride = 1; stride < BLOCK_SIZE; stride *= 2) { __syncthreads(); int index = (threadIdx.x+1)*stride*2 - 1; if(index < 2*BLOCK_SIZE) XY[index] += XY[index - stride];//index is alway bigger than stride __syncthreads();
}
假设BLOCK_SIZE=8, 2*BLOCK_SIZE = 16
stride =1, threadIdx.x+1 = 1,2,3,4...8, stridek index = 1,3,5,7...15, 第一层thread0 ...thread7都执行计算
stride =2, threadIdx.x+1 = 1,2,3,4...8, stridek index = 3,7,11.....31, 第二层thread0 ...thread3都执行计算
stride =3, threadIdx.x+1 = 1,2,3,4...8, stridek index = 5,11,19...47, 第三层thread0 ,thread1都执行计算
stride =4, threadIdx.x+1 = 1,2,3,4...8, stridek index = 7,23,11.....31, 第四层thread0 都执行计算.
我们用Reduction方法得到了一个输出向量,其元素为图中黄色的元素。这个输出向量只包含了部分的最终结果,这8个元素中元素0,1,3, 7计算结束,因此还需要对其进行处理。未得到最终结果的原因是因为有部分的元素对始终没有得到相加的机会,因此接下来需要将缺失的加法计算补充进去。我们这里使用一个逆Reduction方法,也就是第二个步骤:
2.Reduction Reverse Phase
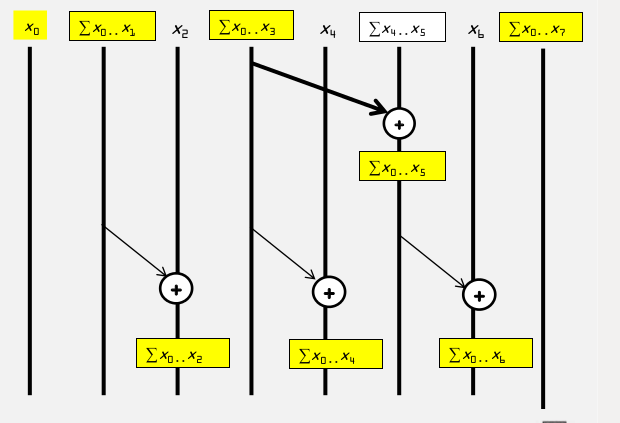
reduction reverse phase kernel代码:
for (unsigned int stride = BLOCK_SIZE/2; stride > 0 ; stride /= 2) { __syncthreads(); int index = (threadIdx.x+1)*stride*2 - 1; if((index+stride)< 2*BLOCK_SIZE) XY[index + stride] += XY[index];
}
假设BLOCK_SIZE=8, 2*BLOCK_SIZE = 16
stride =4, threadIdx.x+1 = 1,2,3,4...8, stridek index = 7,23,11.....31, 第一层thread0执行计算,计算element5
stride =2, threadIdx.x+1 = 1,2,3,4...8, stridek index = 3,7,11.....31, 第二层thread0 ...thread2都执行计算
stride =1, threadIdx.x+1 = 1,2,3,4...8, stridek index = 1,3,5,7...15,, 第三层thread0 ,thread4都执行计算
这一步骤可以计算出:
把这两个步骤合并到一起来看:
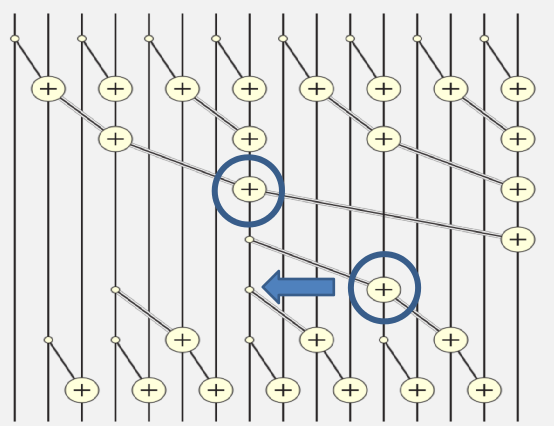
注意上图中已经是16元素的向量了,而不是8元素。从上图可以看到,逆Reduction第一步补充了Reduction中倒数第二步,依此类推,逆Reduction最后一步补充了Reduction中第一步,至此,所有的元素都得到了相加。
容易看出,上述算法总共需要2 * O(logN)步,以及O(N)次加法操作。相比之前的并行算法,得到了很大的优化。
kernel代码
__global__ void work_efficient_scan_kernel(float *X, float *Y, int InputSize) { // XY[2*BLOCK_SIZE] is in shared memory _shared__ float XY[BLOCK_SIZE * 2]; int i = blockIdx.x*blockDim.x + threadIdx.x; if (i < InputSize) {XY[threadIdx.x] = X[i];} // the code below performs iterative scan on XY for (unsigned int stride = 1; stride <= BLOCK_SIZE; stride *= 2) { __syncthreads(); int index = (threadIdx.x+1)*stride*2 - 1; if(index < 2*BLOCK_SIZE) XY[index] += XY[index - stride];//index is alway bigger than stride __syncthreads(); } // threadIdx.x+1 = 1,2,3,4.... // stridek index = 1,3,5,7... for (unsigned int stride = BLOCK_SIZE/2; stride > 0 ; stride /= 2) { __syncthreads(); int index = (threadIdx.x+1)*stride*2 - 1; if(index < 2*BLOCK_SIZE) XY[index + stride] += XY[index]; } __syncthreads(); if (i < InputSize) Y[i] = XY[threadIdx.x]; }