题解「GZOI2019 旧词」

链接

LOJ 3088

Luogu P5305

题意

给定一棵 (n) 个点的有根树，节点标号 (1 sim n)，(1) 号节点为根。
给定常数 (k)。
给定 (Q) 个询问，每次询问给定 (x,y)。
求：

[sumlimits_{i le x} ext{depth}( ext{lca}(i,y))^k ]

( ext{lca}(x,y)) 表示节点 (x) 与节点 (y) 在有根树上的最近公共祖先。
( ext{depth}(x)) 表示节点 (x) 的深度，根节点的深度为 (1)。
由于答案可能很大，你只需要输出答案模 (998244353) 的结果。

( exttt{Data Range:}1leq n leq 5 imes 10^4,1leq q leq 5 imes 10^4)。

题解

考虑一下这个问题的弱化版，即 [LNOI2014]LCA。

求：

[sum_{ileq x} ext{depth}( ext{lca}(i,y)) ]

可以想到最暴力的方法，依次将 (i,y) 上的路径染色，求 ( ext{lca})。

这样我们可以发现一个性质，(y) 的 ( ext{lca}) 一定在从根节点 (1) 到 (y) 的路径上，(i) 的 ( ext{lca}) 也一定在点 (i) 到根节点 (1) 的路径上。并且进一步可以得出，( ext{lca}(i,y)) 就在两者路径的公共部分上，并且就是这个公共部分所包含的深度最大的点。正确性显然。

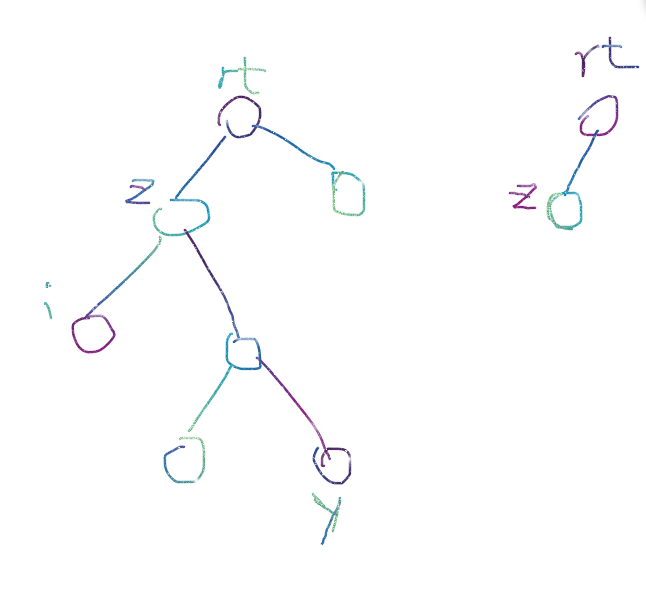
例如，在上图中，点 (i) 到根节点 (1) 的路径与点 (y) 到根节点 (1) 的路径的公共部分，就为根节点 (1) 到点 (z) 的路径，并且 ( ext{lca}(i,y)=z)。

回想一下上面的性质，点 (i) 到根节点 (1) 与点 (y) 到根节点 (1) 的公共路径所包含的深度最大的点 就是 ( ext{lca}(i,y))，那么我们先对从根节点 (1) 到每个点 (i) 的路径染色，再查询根节点 (1) 到点 (y) ，就相当于取了这些公共路径，问题是如何查询 点 (y) 到根节点 (1) 的路径 与 点 (i) 到根节点 (1) 的路径 的公共部分的深度最大的节点的 深度？

可以想到差分，设 (b[x]= ext{depth}(x)- ext{depth}(fa[x]))，则 ( ext{depth}(x)) 即为从 (1) 到点 (x) 的路径上所有(b[j]) 和。由于此弱化版求解的是一个幂为 (1) 的情况，所以 (forall xgeq 1,b[x]=1)。

通过上述结论可以得到，对于每一个 (i) ，将它到根节点 (1) 的路径上的所有点 (j) 的权值加上 (b[j])（(j) 是点 (i) 到根节点 (1) 的路径上包含的点），查询时直接查询点 (y) 到根节点 (1) 的点权和，即为每次询问的答案。

对于此弱化版问题，区间加 (b[j]) 可直接视为区间 (+1)。

但对于此题，要求求解 (k) 次方，应令 (b[x]= ext{depth}(x)^k- ext{depth}(fa[x])^k)。需要维护一个对于每个 (xin [l,r])，点权 (val[x]=val[x]+b[x]) 的操作，其实也非常简单，对 (b[i]) 做前缀和，进行此操作时在线段树上直接加上对应的和即可。

每次询问不是 (n log^2 n) 的么？没看出比暴力优秀多少啊？

我们可以将询问离线，将 (x) 从小到大排序，保证每次询问时都维护了点 (1sim x) 的贡献（当前询问的 (x)）并统计答案。这样保证每个点到根节点 (1) 的路径只会在树上被操作一次，减少了冗余操作。其实就是个 (one-pointer)，很好理解。

经过上述分析，对于该题，我们需要一个支持路径修改，路径查询的数据结构，使用 树链剖分+线段树 即可。时间复杂度为 (O(n+q log^2 n))。

Show the Code

#include<cstdio>
#include<algorithm>
typedef long long ll;
const ll mod=998244353;
int tot=0,cnt=0;
int h[500005],to[500005],ver[500005];
int d[500005],fa[500005],size[500005],son[500005];
int seg[500005],rev[500005],top[500005];
ll sum[2000005],tag[2000005],b[500005],ans[500005];
struct node {int x,y,id;} q[500005];
inline void swap(int &x,int &y) {int tmp=y;y=x;x=tmp;}
inline bool cmp(node x,node y) {return x.x<y.x;}
inline ll Add(ll x,ll y) {return (((x+y)%mod)+mod)%mod;}
inline ll read() {
	register ll x=0,f=1;register char s=getchar();
	while(s>'9'||s<'0') {if(s=='-') f=-1;s=getchar();}
	while(s>='0'&&s<='9') {x=x*10+s-'0';s=getchar();}
	return x*f;
}
inline void add(int x,int y) {
	to[++cnt]=y;
	ver[cnt]=h[x];
	h[x]=cnt;
}
inline ll qpow(ll x,ll p) {
	ll res=1;
	for(;p;p>>=1) {
		if(p&1) res=res*x%mod;
		x=x*x%mod;
	}
	return res;
}
inline void dfs1(int x) {
	size[x]=1;son[x]=-1;
	for(register int i=h[x];i;i=ver[i]) {
		int y=to[i];
		d[y]=d[x]+1;fa[y]=x;
		dfs1(y);size[x]+=size[y];
		if(son[x]==-1||size[son[x]]<size[y]) son[x]=y;
	}
}
inline void dfs2(int x,int t) {
	seg[x]=++tot;rev[tot]=x;top[x]=t;
	if(son[x]!=-1) dfs2(son[x],t);
	for(register int i=h[x];i;i=ver[i]) {
		int y=to[i];
		if(y==son[x]) continue;
		dfs2(y,y);
	}
}
inline void work(int p,int l,int r,ll val) {
	val%=mod;
	tag[p]=Add(tag[p],val);
	sum[p]=Add(sum[p],val*Add(b[r],-b[l-1]));
}
inline void spread(int p,int l,int r) {
	if(tag[p]) {
		int mid=l+r>>1;
		work(p<<1,l,mid,tag[p]);
		work(p<<1|1,mid+1,r,tag[p]);
		tag[p]=0;
	}
}
inline void change(int p,int L,int R,int l=1,int r=tot) {
	if(L<=l&&r<=R) {work(p,l,r,1);return;}
	spread(p,l,r);
	int mid=l+r>>1;
	if(L<=mid) change(p<<1,L,R,l,mid);
	if(R>mid) change(p<<1|1,L,R,mid+1,r);
	sum[p]=sum[p<<1]+sum[p<<1|1];
}
inline ll ask(int p,int L,int R,int l=1,int r=tot) {
	if(L<=l&&r<=R) return sum[p];
	spread(p,l,r);
	int mid=l+r>>1;ll res=0;
	if(L<=mid) res=Add(res,ask(p<<1,L,R,l,mid));
	if(R>mid) res=Add(res,ask(p<<1|1,L,R,mid+1,r));
	return res;
}
inline void Modify(int x,int y) {
	while(top[x]!=top[y]) {
		if(d[top[x]]<d[top[y]]) swap(x,y);//d[top[x]]>=d[top[y]]
		change(1,seg[top[x]],seg[x]);
		x=fa[top[x]];
	}
	if(d[x]>d[y]) swap(x,y);//d[x]<=d[y]
	change(1,seg[x],seg[y]);
}
inline ll Qsum(int x,int y) {
	ll res=0;
	while(top[x]!=top[y]) {
		if(d[top[x]]<d[top[y]]) swap(x,y);
		res=Add(res,ask(1,seg[top[x]],seg[x]));
		x=fa[top[x]];
	}
	if(d[x]>d[y]) swap(x,y);//d[x]<=d[y]
	return Add(res,ask(1,seg[x],seg[y]));
}
int main() {
	int n=read(),T=read(),k=read();
	for(register int i=2;i<=n;++i) add(read(),i);
	for(register int i=1;i<=T;++i) {q[i].x=read();q[i].y=read();q[i].id=i;}
	std::sort(q+1,q+1+T,cmp);
	d[1]=1;dfs1(1);dfs2(1,1);//printf("%d
",tot);
	for(register int i=1;i<=tot;++i) {int x=rev[i];b[i]=Add(b[i-1],qpow(d[x],k)-qpow(d[fa[x]],k)+mod);}
	int now=1;
	for(register int i=1;i<=T;++i) {
		while(now<=q[i].x) {Modify(1,now);++now;}
		ans[q[i].id]=Qsum(1,q[i].y);
	}	
	for(register int i=1;i<=T;++i) printf("%lld
",ans[i]);
	return 0;
}