RL实践1——值迭代求解随机策略
参考自叶强《强化学习》第三讲,方格世界—— 使用 动态规划 求解随机策略
动态规划的使用条件时MDP已知,在简单游戏中,这个条件时显然成立的
使用Value iteration的方法求解每个状态的价值函数,迭代收敛之后,对应最优策略生成。
注意:动态规划和强化学习都用的价值函数,区别在于
- 动态规划需要基于模型获取采取动作后下一时刻的状态,已进行评估,需要MDP模型已知;
- 强化学习无模型的学习方法,可以基于采样,对episode的状态(动作)价值函数进行学习。
问题定义
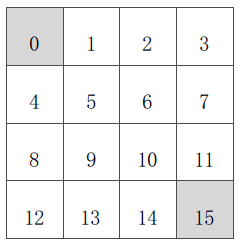
从方格状态走到终止状态(灰色标记)
Python代码及注释
值得注意的是,知乎原版的注释是错误的,采用的是同步更新
有三个trick可以加快运算速度(对于大规模问题)
- in-place DP:新值直接替换旧值,只存储一个v(s),
- 异步更新,提高效率
- 缺点:更新顺序影响收敛性
- Prioritised sweeping:state的影响力排序
- 比较贝尔曼误差绝对值,大的更新,小的忽略
- Real-time DP:遍历过的才更新
- 省去了agent 未遍历的状态s,对于稀疏任务效率提升极大
# 状态集合
states = [i for i in range(16)]
# 价值集合
values = [0 for _ in range(16)]
# 动作集:
actions = ["n", "e", "s", "w"]
# 动作字典:
ds_actions = {"n": -4, "e": 1, "s": 4, "w": -1}
# 衰减率
gamma = 1.00
# 定义MDP
def nextState(s, a):
next_state = s
if (s%4 == 0 and a == "w") or (s<4 and a == "n") or
((s+1)%4 == 0 and a == "e") or (s > 11 and a == "s"):
pass
else:
ds = ds_actions[a]
next_state = s + ds
return next_state
# 定义奖励
def rewardOf(s):
return 0 if s in [0, 15] else -1
# 判断是否结束
def isTerminateState(s):
return s in [0, 15]
# 获取所有可能的next state 集合
def getSuccessors(s):
successors = []
if isTerminateState(s):
return successors
for a in actions:
next_state = nextState(s, a)
# if s != next_state:
successors.append(next_state)
return successors
# 更新当前位置的价值函数
def updateValue(s):
sucessors = getSuccessors(s)
newValue = 0 # values[s]
num = 4 # len(successors)
reward = rewardOf(s)
for next_state in sucessors:
newValue += 1.00 / num * (reward + gamma * values[next_state])
return newValue
# 打印所有状态对应价值函数
def printValue(v):
for i in range(16):
print('{0:>6.2f}'.format(v[i]), end=" ")
if (i + 1) % 4 == 0:
print("")
print()
# 一次迭代
# 这里采用的是同步更新,不是异步更新。创建了newvalues数组,遍历过states后,统一更新global values
def performOneIteration():
newValues = [0 for _ in range(16)]
for s in states:
newValues[s] = updateValue(s)
global values
values = newValues
printValue(values)
# 主函数
def main():
max_iterate_times = 160
cur_iterate_times = 0
while cur_iterate_times <= max_iterate_times:
print("Iterate No.{0}".format(cur_iterate_times))
performOneIteration()
cur_iterate_times += 1
printValue(values)
if __name__ == '__main__':
main()
运算结果如下
Iterate No.0
0.00 -1.00 -1.00 -1.00
-1.00 -1.00 -1.00 -1.00
-1.00 -1.00 -1.00 -1.00
-1.00 -1.00 -1.00 0.00
Iterate No.1
0.00 -1.75 -2.00 -2.00
-1.75 -2.00 -2.00 -2.00
-2.00 -2.00 -2.00 -1.75
-2.00 -2.00 -1.75 0.00
.
.
.
Iterate No.158
0.00 -14.00 -20.00 -22.00
-14.00 -18.00 -20.00 -20.00
-20.00 -20.00 -18.00 -14.00
-22.00 -20.00 -14.00 0.00
Iterate No.159
0.00 -14.00 -20.00 -22.00
-14.00 -18.00 -20.00 -20.00
-20.00 -20.00 -18.00 -14.00
-22.00 -20.00 -14.00 0.00
Iterate No.160
0.00 -14.00 -20.00 -22.00
-14.00 -18.00 -20.00 -20.00
-20.00 -20.00 -18.00 -14.00
-22.00 -20.00 -14.00 0.00
0.00 -14.00 -20.00 -22.00
-14.00 -18.00 -20.00 -20.00
-20.00 -20.00 -18.00 -14.00
-22.00 -20.00 -14.00 0.00