nowcoder 203A Knight（贪心+打表）

题目链接

题目描述

有一张无限大的棋盘，你要将马从(0,0)移到(n,m)。
每一步中，如果马在(x,y)，你可以将它移动到(x+1,y+2),(x+1,y-2),(x-1,y+2),(x-1,y-2),(x+2,y+1),(x+2,y-1),(x-2,y+1)或(x-2,y-1)。
你需要最小化移动步数。

输入描述:

第一行一个整数t表示数据组数 (1≤ t≤ 1000)。
每组数据一行两个整数n,m (|n|,|m|≤ 10$$$^9$$$)。

输出描述:

每组数据输出一行一个整数表示最小步数。

输入

2
0 4
4 2

输出

2
2

题意

使用最少步数把“马”从(0,0)走到(n,m)

分析

遇事不决先打个表。（请原谅我的作图水平，原点在左上角）

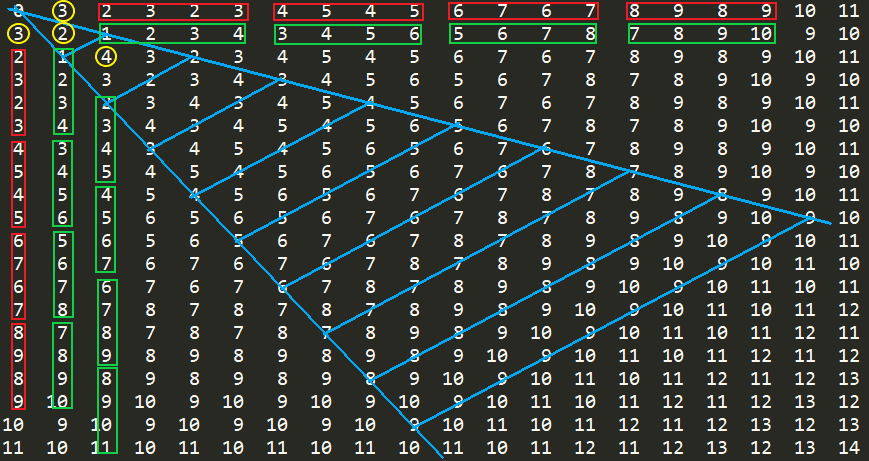
最先发现当n+m=3k时，只用k步就能走到，但前提是每走一步，马和终点的曼哈顿距离都减少3，因此只对介于n=2m和m=2n之间的点满足。
有了这个性质以后，进一步还可以发现，在分界线内部，贪心地走，n+m=3k+1上的点只需要从n+m=3k上的点再走一步就能到，n+m=3k+2上的点从n+m=3k上的点再走两步就能到。所以，求解介于n=2m和m=2n之间的点完成了。
以上是在打表之前分析出来，打表之后得到验证的，接下来是分界线外部的点，打表后意外发现是以4个为整体在有规律的变化。

• 当n=0时，从m=2开始形成循环节，假设用p表示m在第几节，r表示m是节内第几个，那么p=(m-2)/4，r=(m-2)%4，(0,m)的值就是2+2p+(r&1);
• 当n>0时，从m=2n开始形成循环节，同样求出p=(m-2n)/4，r=(m-2n)%4，那么(n,m)的值就是n+2p+r;

因为n和m对称求解方法是一样的，所以求解边界外的点也完成了（还有四个特例需要特判一下）。
PS：(2,2)很特殊，它不能在n+m=3的基础上，再一步走到的原因是，它需要的点位于(3,0)和(0,3)，而这两个点超出了边界，但对于其他点是都能在n+m=3k上找到点的。

总结

看不懂标答怎么办，好像在乱搞的路上越走越远了

代码

#include<stdio.h>
int main() {
    int T, n, m;
    int px, rx;
    for (scanf("%d", &T); T; T--) {
        scanf("%d %d", &n, &m);
        if (n<0)n = -n; if (m<0)m = -m;
        if (n + m == 0)printf("0
");
        else if (n + m == 1)printf("3
");
        else if (n == 1 && m == 1)printf("2
");
        else if (n == 2 && m == 2)printf("4
");
        else if (m <= 2 * n&&n <= 2 * m)
            printf("%d
", (m + n) / 3 + (m + n) % 3);
        else if (m == 0) {
            px = (n - 2) / 4, rx = (n - 2) % 4;
            printf("%d
", 2 * px + 2 + (rx & 1));
        }
        else if (n == 0) {
            px = (m - 2) / 4, rx = (m - 2) % 4;
            printf("%d
", 2 * px + 2 + (rx & 1));
        }
        else if (m>2 * n) {
            px = (m - 2 * n) / 4, rx = (m - 2 * n) % 4;
            printf("%d
", n + px * 2 + rx);
        }
        else if (n>2 * m) {
            px = (n - 2 * m) / 4, rx = (n - 2 * m) % 4;
            printf("%d
", m + px * 2 + rx);
        }
    }
}