1.1 二行列式的性质:
- 性质1. 行列互换,二阶行列式的值不变。
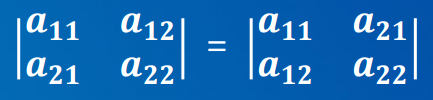
- 性质2. 二阶行列式中某行(列)每个元素分成2个数之和,则该行列式可关于该行(列)拆开成2个行列之和,拆开时其他行保持不变。
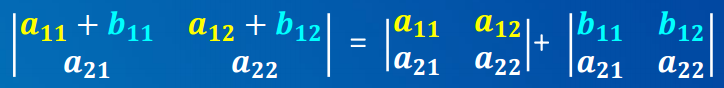
- 性质3. 两行(列)互换,行列式的值变号。
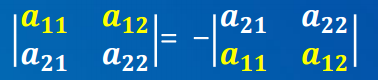
- 性质4. 二阶行列式中某行(列)有公因子k时,k可以提出共因式外。

- 性质5. 二阶行列式中某一行(列)加上另一行/列的k倍时,其值不变。
-
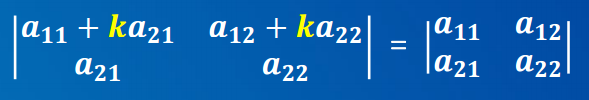
1.2 三阶展开式:
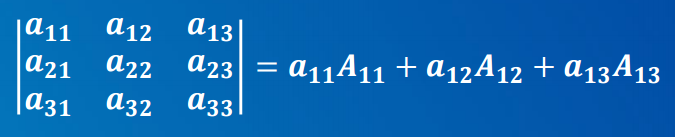
定理:2、3阶行列式等于它的任一行 (或列) 元素与自己的代数余子式 乘积之和.
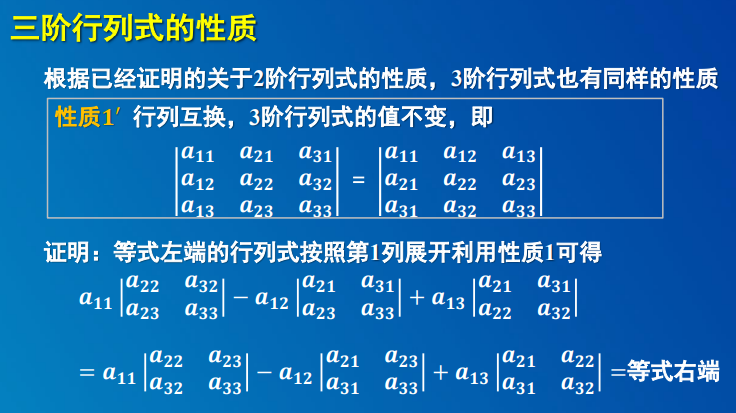
1.3 三阶行列式性质: 与二阶相同。
2.1 n元排列的逆序数:在一个n元排列 j1 j2 …… jn中,如果一个大数排在小数前面,即当s<t时,有js>jt,则称这一对数jsjt构成一个逆序,此排列的逆序总数称为它的逆序数。例如: 5元排列 23541 中,21, 31, 54, 51, 41为所有逆序,故τ(23541)=5。 下标是j后的数字,如a11a22a34a43的下标为1243。
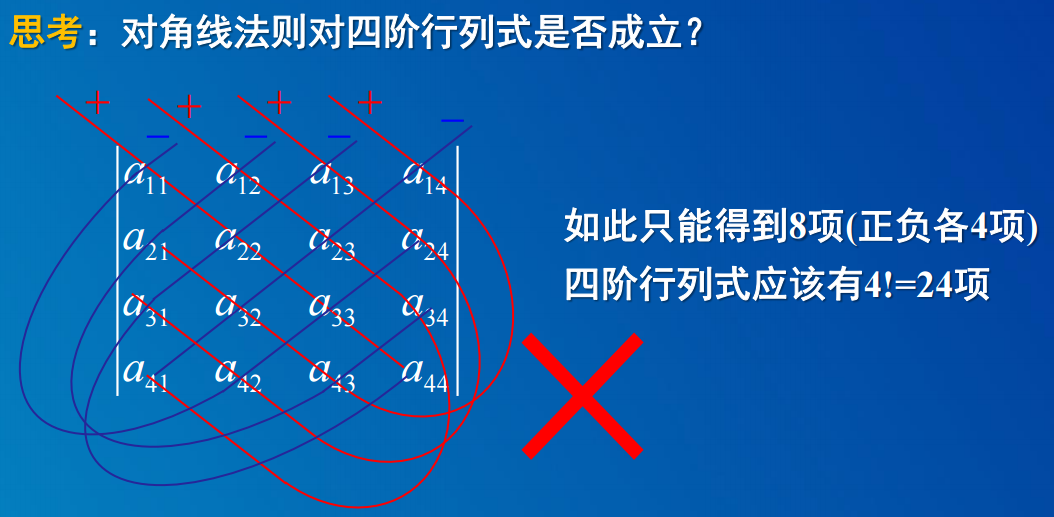
注:S为下标集合。而n元全排列的代数和为Pn=n!,即2阶行列式的代数和为2!=2项,3阶行列式的代数和为3! = 6项。4阶:4! = 24项(不能用对角线的方式求4阶行列式,对角线方式的代数和为8项)。

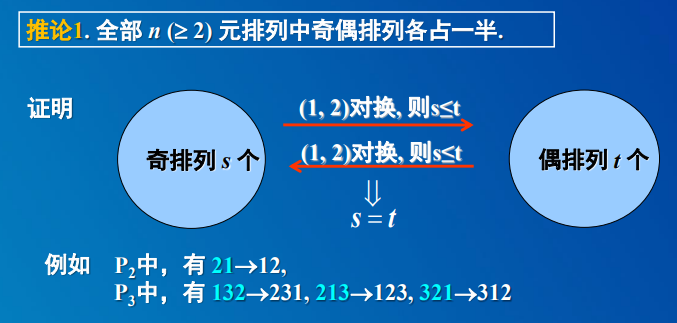
2.2 逆序数的奇偶排列:逆序数为偶数的排列称为偶排列;逆序数为奇数的排列为奇排列。

2.3 对换:在一个排列中把两个数i与j互换位置(无论i,j是否相邻都会导致奇偶性变化)。 对换改变排列奇偶性。

3.1 n阶行列式的定义:

注:不能用对角线的方式求n(n>3)阶行列式,如4阶行列式,对角线方式的代数和为8项,而4阶行列式的代数和为n! = 24项。
3.2 行列式的等价定义:

4.1 行列式的性质
- 性质1 行列式与它的转置行列式相等,即 D = DT.

- 性质2 某列(行)相加可拆项,即“逐行(列)保持加法”或“加法拆项法则”。
-

- 性质3 行列式某一列(或行)的公因子可以提到行列式外
-

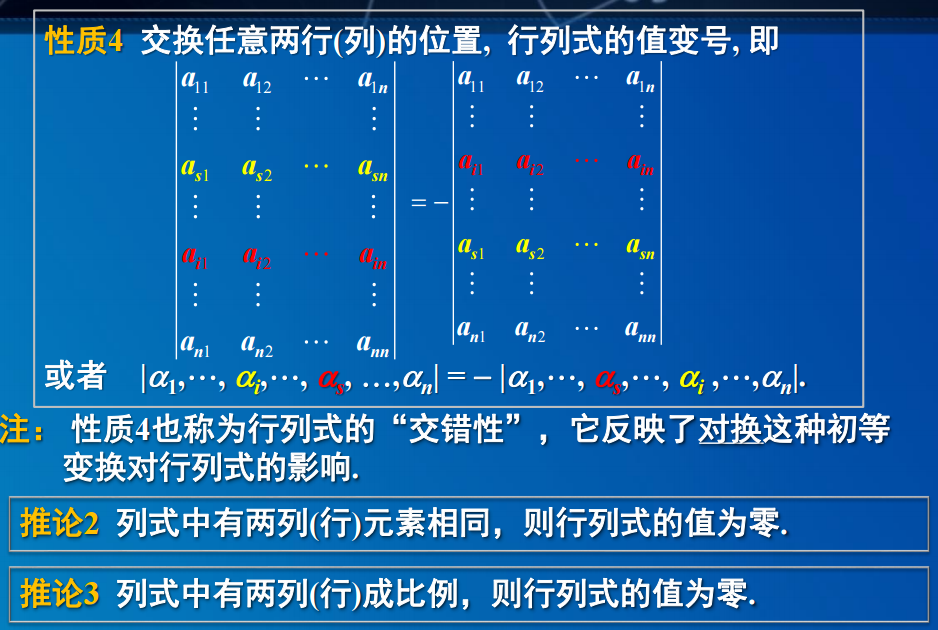
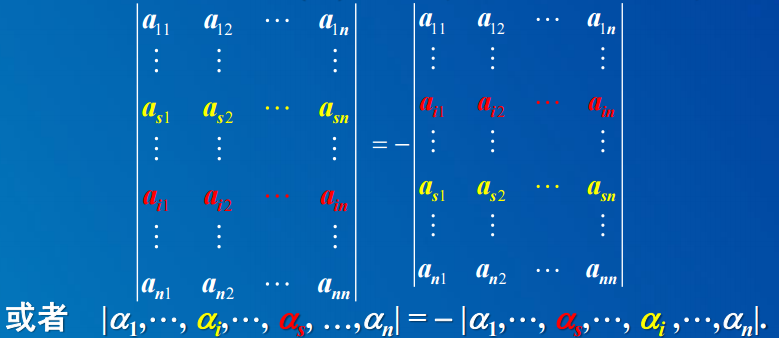
- 性质4 交换任意两行(列)的位置, 行列式的值变号
-
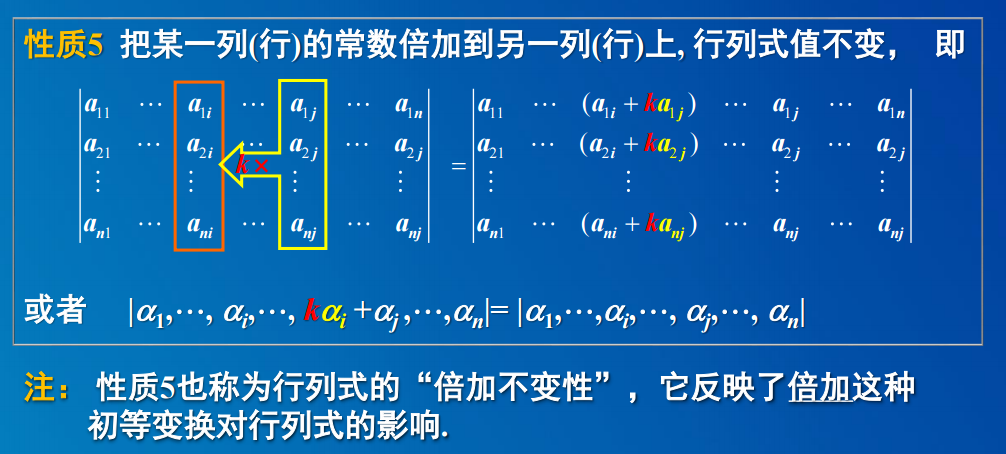
- 性质5 把某一列(行)的常数倍加到另一列(行)上, 行列式值不变
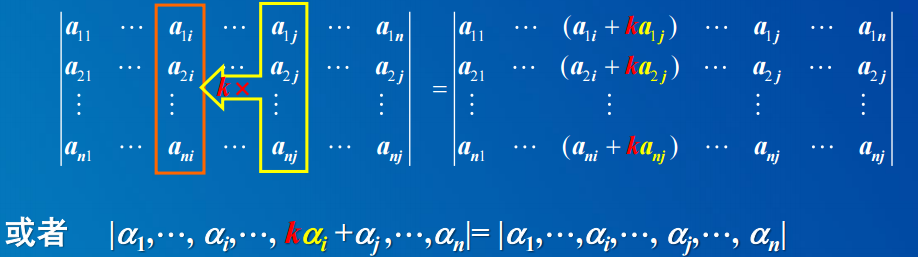
5. 行列式的计算
- 打洞法1:利用初等变换把行列式化为三角行列式
- 行(列)拆项法:把行列式拆分为2的方幂个易于计算的行 列式之和.
6. 行列式的展开公式
在行列式的完全展开式中, 含有n!项,每一项一定包含第1行的一 个元素,即 a11, …, a1k , …, a1n中的某一个.

Mik表示为一个n-1阶行列式。

1. 二阶、三阶行列式的性质













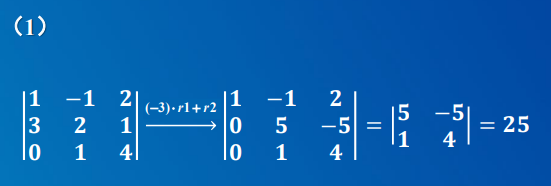

2. n元排列






3. n阶行列式的定义
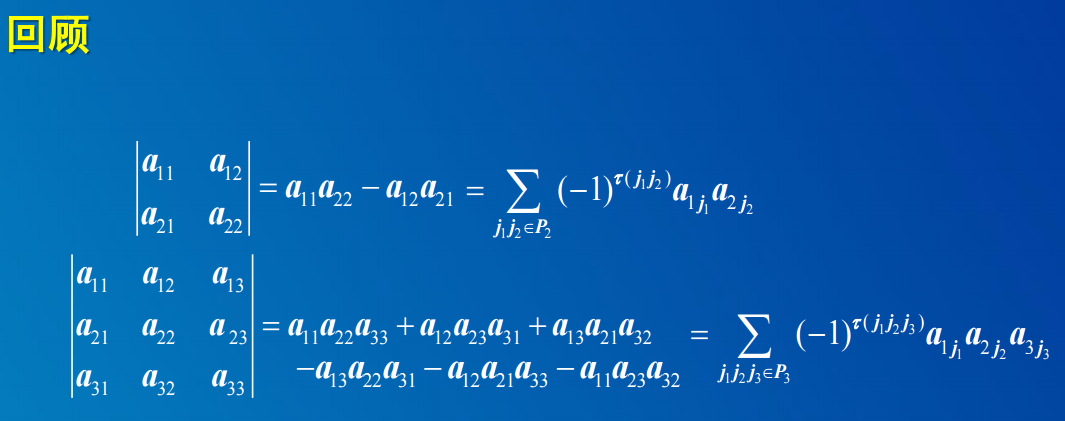











4. 行列式的性质