矩阵向量
总结:
1. 矩阵和线性方程组:A向量*x向量=b向量,Ab为扩展向量。有解:说明b向量可以被A向量线性表示;无解:说明b向量无法被A向量线性表示。
2. 线性方程的行图和列图
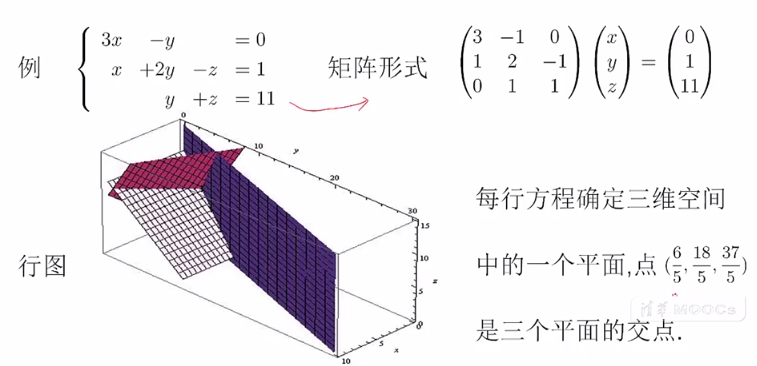
行图:是从坐标系的角度看线性方程,(2元/3元)方程组的每一行代表是一条直线/平面。有解:则在直线/平面间有交点。
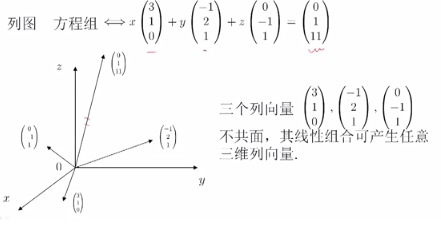
列图:是从矢量的角度看线性方程。
2.1 矩阵与向量的乘积
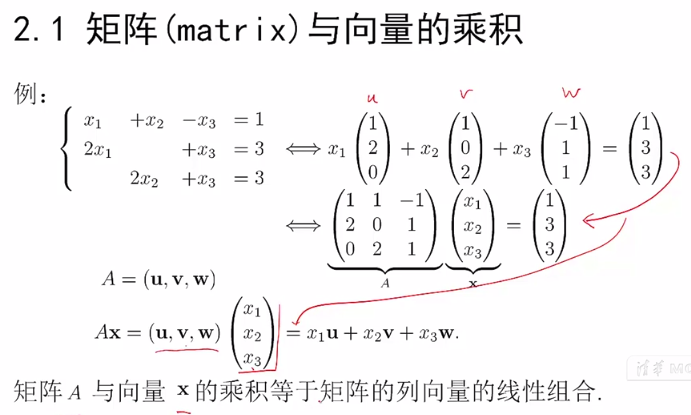
我们可以将系数作为向量提出来,记为u,v,w,3个向量,并把3个向量组成3*3的A矩阵,并把x1,x2,x3做为一个向量,记成X。

上述方程也可以表述为矩阵的每一行与向量X的点乘的方程。


2.2 可逆矩阵
定义:设A为n阶方阵, 若存在n阶方阵B, 使得AB = BA = In, 则称A为可逆矩阵或非奇异矩阵, 而称B 为A 的逆矩阵,并记为A-1.
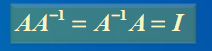
逆矩阵的性质:

逆矩阵与线性方程: Ax = b, 如果b有唯一解,则A是可逆的。(有解说明A与b线性相关)

由于方程有解,b向量可以用A向量线性表示。可以写成下面的的方程:X向量=S向量 * b向量,其中S向量为A向量的逆向量。

向量线性相关性(有解:线性相关;无解:线性无关)

多个向量间线性相关,则其中某个向量可以被其他向量线性表示。




2.3 线性方程组的行图和列图
行图:是从坐标系的角度看线性方程,(2元/3元)方程组的每一行代表是一条直线/平面。
列图:是从矢量的角度看线性方程。
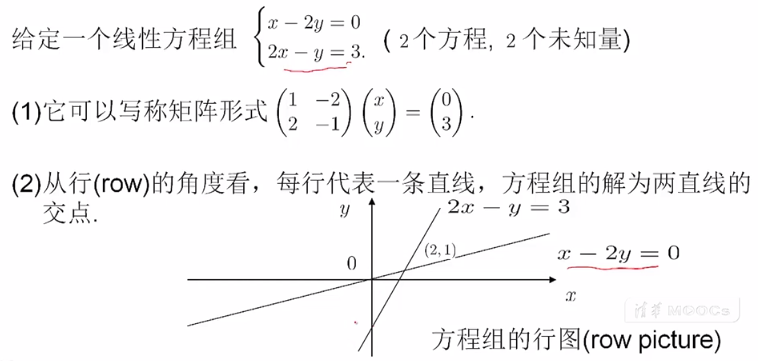


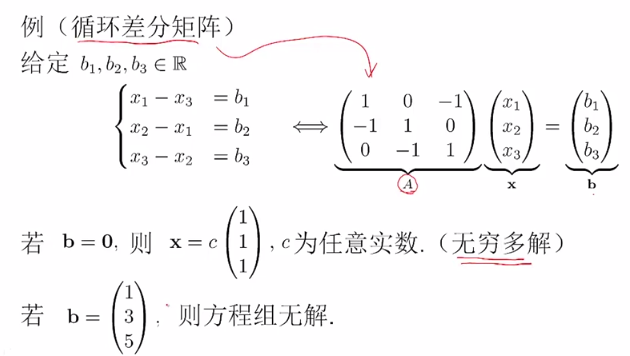
如果方程组有解,则在每行方程组,即这些直线和平面中有交点,无解,则没有交点。有唯一解,则A可逆。

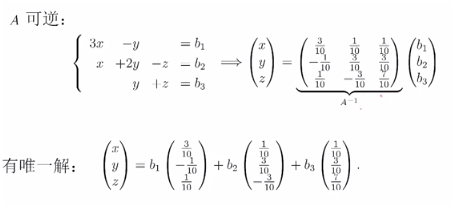
下面例子中,Ab扩展矩阵无解,所以b向量无法被A向量线性表示。A不可逆。
