独立性检验表明的是两者是否有关系,相关性检验说明两者成什么样的关系,无论是否有关系都可以表示出回归方程
1 相关性检验
简单相关系数:度量定量变量间的线性相关关系(非相关性)
复相关系数:因变量与多个自变量之间的关系
偏相关系数:反应矫正其他变量后某一变量与另一变量的相关关系,校正:嘉定其他变量取值均为平均数
典型相关系数:主成分分析后得到性的线性无关的综合指标,通过新的综合指标间的相关系数研究原来的各组指标之间的整体相关性
1.1 皮尔森相关系数
1.1.1 协方差
二维随机变量(X,Y),X与Y之间的协方差定义为(Cov(X,Y) = E{[X - E(X)][Y - E(Y)]})
E为期望
协方差>0,正相关;协方差<0,正相关;协方差=0,不相关
1.1.2 相关系数
相关系数定义:(Corr(X,Y) = frac{Cov(X,Y)}{sqrt{Var(X)}sqrt{Var(Y)}}=frac{Cov(X,Y)}{sigma_x sigma_y});Var为方差
Corr(X,Y)=1的时候,说明两个随机变量完全正相关;Corr(X,Y)=-1的时候,说明两个随机变量完全负相关;Corr(X,Y)为0,表示X与Y不相关,这里的不相关指的是X与Y没有线性关系
2 独立性检验
2.1 卡方独立性检验Chi-Square Test
在大数据运营场景中,通常用在某个变量(或特征)值是不是和应变量有显著关系。
普通的思维方式,是拿已经知道的结果(硬币是均衡的,没有人做过手脚),推测出会出现的不同现象的次数。而卡方检验是拿观察到的现象(投正面或反面的次数或者频数),来判断这个结果(硬币是不是均衡的)。
卡方检验公式为:(chi^2 = sum frac{(observed - expected)^2}{expected})
方法:1.公式求值。2.自由度:假设仅有X1 X2,X1若给定,X2不自由?则自由度为2-1即1。3.置信度:自己设

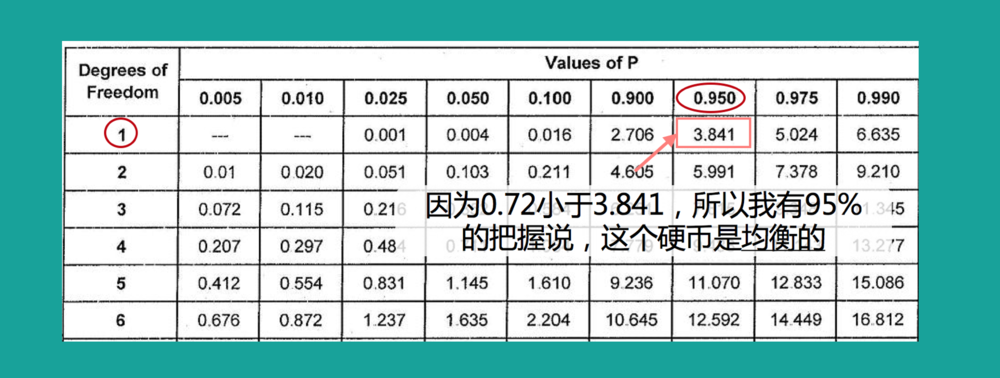
拿到这3个信息,去查表,因为0.72小于查表得到的3.841,所以我们得出这个硬币是均衡的结论。