快速排序(18JavaB5,9’)
以下代码可以从数组a[]中找出第k小的元素。
它使用了类似快速排序中的分治算法,期望时间复杂度是O(N)的。
请仔细阅读分析源码,填写划线部分缺失的内容。
import java.util.Random;
public class Main{
public static int quickSelect(int a[], int l, int r, int k) {
Random rand = new Random();
int p = rand.nextInt(r - l + 1) + l;
int x = a[p];
int tmp = a[p]; a[p] = a[r]; a[r] = tmp;
int i = l, j = r;
while(i < j) {
while(i < j && a[i] < x) i++;
if(i < j) {
a[j] = a[i];
j--;
}
while(i < j && a[j] > x) j--;
if(i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if(i - l + 1 == k) return a[i];
if(i - l + 1 < k) return quickSelect( _________________________________ ); //填空
else return quickSelect(a, l, i - 1, k);
}
public static void main(String args[]) {
int [] a = {1, 4, 2, 8, 5, 7};
System.out.println(quickSelect(a, 0, 5, 4));
}
}
注意:只提交划线部分缺少的代码,不要抄写任何已经存在的代码或符号。
先看看典型的快速排序
快速排序
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序
它采用了一种分治(Divide-and-ConquerMethod)的策略
基本思想
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
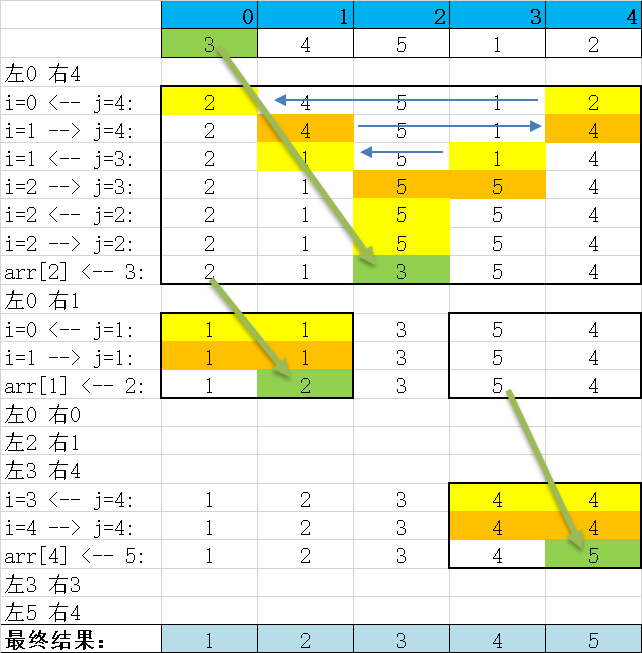
先把基准值(最左)存起来
高位(右)大的往左边拉
低位(左)小的往右边拉
最后,存的那个基准值(曾经最左)放中间
对左:相同处理
对右:相同处理
package bb;
public class QuickSortMy {
static void printArray(int a[]) {
for (int i : a) {
System.out.print(i + " ");
}
System.out.println();
}
static void qsort(int a[], int left, int right) {
if (left >= right) {
return;
}
printArray(a);
int key = a[left];
int i = left, j = right;
while (i < j) {
while (i < j && a[j] > key) {
j--;
}
if (i < j) {
System.out.printf("a[%d]=%d <- a[%d]=%d
", i, a[i], j, a[j]);
a[i++] = a[j];
}
while (i < j && a[i] < key) {
i++;
}
if (i < j) {
System.out.printf("a[%d]=%d -> a[%d]=%d
", i, a[i], j, a[j]);
a[j--] = a[i];
}
}
a[i] = key;
printArray(a);
qsort(a, left, i - 1);
qsort(a, i + 1, right);
}
public static void main(String[] args) {
int a[] = { 3, 4, 5, 1, 2 };
qsort(a, 0, a.length - 1);
}
}
2018JavaB组第5题的参考答案+注释如下所示:
package bb;
import java.util.Random;
public class JB18_5快速排序 {
public static int quickSelect(int a[], int l, int r, int k) {
Random rand = new Random();
int p = rand.nextInt(r - l + 1) + l;
int x = a[p];
int tmp = a[p];
a[p] = a[r];
a[r] = tmp;
int i = l, j = r;
while (i < j) {
while (i < j && a[i] < x)
i++;
if (i < j) {
a[j] = a[i];
j--;
}
while (i < j && a[j] > x)
j--;
if (i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if (i - l + 1 == k)// (1)说明到底了
return a[i];
if (i - l + 1 < k)
return quickSelect(a, i + 1, r, k - i + l - 1); // 填空
// qsort(a, i + 1, right);
// (3)先试试k,
// (4)再考虑:k要移动到等于(i - l + 1),试试k-(i - l + 1)
else
// i - l + 1 > k
return quickSelect(a, l, i - 1, k);// (2)qsort(a, left, i -
// 1);对上了,k不变
}
public static void main(String args[]) {
int[] a = { 1, 4, 2, 8, 5, 7 };
System.out.println(quickSelect(a, 0, 5, 4));
// int [] a = {1, 4, 2, 8, 5, 7, 23, 58, 16, 27, 55, 13, 26, 24, 12, 2};
// System.out.println(quickSelect(a, 0, a.length-1, 6));
}
}