给定数组arr,arr中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim代表要找的钱数,求换钱有多少种方法。
arr=[5,10,25,1],aim=0。组成0元的方法有1种,就是所有面值的货币都不用。所以返回1。arr=[5,10,25,1],aim=15。组成15元的方法有6种,分别为3张5元、1张10元+1张5元、1张10元+5张1元、10张1元+1张5元、2张5元+5张1元和15张1元。所以返回6。arr=[3,5],aim=2。任何方法都无法组成2元。所以返回0。
暴力解
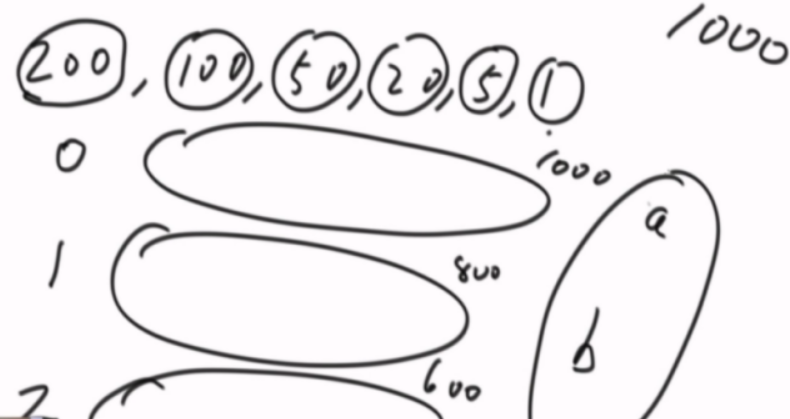
使用0张200的,后面凑出1000的方法数a
使用1张200的,后面凑出 800的方法数b
使用2张200的,后面凑出 600的方法数c
a+b+c全部加起来就是答案。
优化:记忆化搜索
如果index和aim固定的,只要是后面要计算600那返回值一定是确定的,是个无后效性问题,前面怎么选择不影响后面的操作。但是返回值一样都要重复计算,利用一个map存储之前的结果(缓存)。下次调用,直接取出,不用这么暴力的重复计算。
动态规划
参数的变化可以囊括返回值的变化,分析可变参数的变化范围
- 目标(主函数调用的递归入口)
- 确定不依赖其他位置的值(递归中的basecase,递归出口)
- 位置依赖(调递归过程,下一次调用递归的参数)
- 优化:当前位置的下一排相同位置及左边的位置
arr[5,3,2],求组成10的方法总数(表格中每一行的值:当前面值组成当前钱数的方法总数)
| 钱的面值 | 位置(数组中的下标) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 目标钱数(aim) |
| 5 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 4 | |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | |
| 2 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
//给定一些面值的钱(每种钱任意张),求用这些钱组成目标钱数的方法数 #include <iostream> #include <vector> #include <string> #include <map> using namespace std; //1.暴力递归 //index:可以任意使用index及其之后的钱 //aim:要找的目标钱数 int get_num_solution(const vector<int> &arr,int index,int aim) { //如果inde==数组的长度,aim还有剩余,那么之前的选择不是有效的res=0 if(index==arr.size()) return aim==0?1:0; int res=0; for(int i=0;arr.at(index)*i<=aim;++i)//一直在选择,此次的选择是否有效,无效后面返回0 res+=get_num_solution(arr,index+1,aim-arr.at(index)*i); return res; } //2.优化版---记忆化搜索 //index和aim固定,返回值一定是固定的(无后效性问题):到达一个状态,这个状态和到达它的路径无关,返回值和怎么到达它的无关 //index和aim确定返回值 //key:index_aim value:返回值 map<string,int> m;//缓存 int get_num_solution1(const vector<int>& arr, int index, int aim) { if(index==arr.size()) return aim==0?1:0; int res=0; string key; for(int i=0;arr.at(index)*i<=aim;++i) { int nextAim=aim-arr.at(index)*i; key=to_string(index+1).append("_").append(to_string(nextAim));//下一层递归的key if(m.count(key)==1) res+=m.at(key); else res+=get_num_solution(arr,index+1,nextAim); } key=to_string(index).append("_").append(to_string(aim)); m.insert({key,res}); return res; } //3.动态规划 int get_num_solution2(const vector<int>& arr,int aim) { vector<vector<int> > dp(arr.size(),vector<int>(aim+1,0)); //第一列 for(int i=0;i<arr.size();++i) dp.at(i).at(0)=1; for(int j=1;arr.at(0)*j<=aim;++j) dp.at(0).at(arr.at(0)*j)=1; for(int i=1;i<arr.size();++i) { for(int j=1;j<=aim;++j) { dp.at(i).at(j)=dp.at(i-1).at(j); dp.at(i).at(j)+=j-arr.at(i)>=0?dp.at(i).at(j-arr.at(i)):0; } } return dp.at(arr.size()-1).at(aim); } int main() { vector<int> a{5,3,2};//{5,10,25,1}; cout<<get_num_solution(a,0,10)<<endl; cout<<get_num_solution1(a,0,10)<<endl; cout<<get_num_solution2(a,10)<<endl; return 0; }
例题一:(排成一条线的纸牌博弈问题)
给定一个整型数组arr,代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌,规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左或最右的纸牌,玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。
例:
arr=[1,2,100,4]。开始时玩家A只能拿走1或4。如果玩家A拿走1,则排列变为[2,100,4],接下来玩家B可以拿走2或4,然后继续轮到玩家A。如果开始时玩家A拿走4,则排列变为[1,2,100],接下来玩家B可以拿走1或100,然后继续轮到玩家A。玩家A作为绝顶聪明的人不会先拿4,因为拿4之后,玩家B将拿走100。所以玩家A会先拿1,让排列变为[2,100,4],接下来玩家B不管怎么选,100都会被玩家A拿走。玩家A会获胜,分数为101。所以返回101。
arr=[1,100,2]。开始时玩家A不管拿1还是2,玩家B作为绝顶聪明的人,都会把100拿走。玩家B会获胜,分数为100。所以返回100。
#include <iostream> #include <vector> #include <cmath> using namespace std; int s(const vector<int> &a,int i,int j); int f(const vector<int> &a,int i,int j) { //如果i == j,即a[i...j]上只有一张纸牌,当然会被先拿纸牌的人拿走,所以可以返回a[i]; if(i==j) return a.at(i); //拿了其中一个之后,当前玩家成了后拿的那个人,因为当前的玩家会做出最好的选择,所以会拿走最好的 return max((a.at(i)+s(a,i+1,j)),(a.at(j)+s(a,i,j-1))); } int s(const vector<int> &a,int i,int j) { //如果i == j,即a[i...j]上只有一张纸牌,作为后拿的人必然什么也得不到,所以返回0 if(i==j) return 0; //因为对手会拿走最好的,所以当前玩家只能拿最差的 return min(f(a,i+1,j),f(a,i,j-1)); } //1.暴力 int win(const vector<int> &a) { return max(f(a,0,a.size()-1),s(a,0,a.size()-1)); } //2.动态规划 int win1(const vector<int>& a) { if(a.empty()||a.size()<=0) return -1; vector<vector<int> > f(a.size(),vector<int>(a.size(),0)); vector<vector<int> > s(a.size(),vector<int>(a.size(),0)); for(int j=0;j<a.size();++j) { f.at(j).at(j)=a.at(j); for(int i=j-1;i>=0;--i) { f.at(i).at(j)=max(a.at(i)+s.at(i+1).at(j),a.at(j)+s.at(i).at(j-1)); s.at(i).at(j)=min(f.at(i+1).at(j),f.at(i).at(j-1)); } } return max(f.at(0).at(a.size()-1),s.at(0).at(a.size()-1)); } int main() { vector<int> v{1,2,100,4}; cout<<win(v)<<endl; cout<<win1(v)<<endl; return 0; }
例题二:
一个长度为N的路,1~N。一个机器人在M位置,他可以走P步,如果在1只能走右,在N只能走左,请问机器人走P步后他停在K位置上的走法有多少种。
思路:
可变参数是M(机器人位置)和P(可以走的步数),最后需要获取的位置是(M,P),找到普遍依赖,发现是一个杨辉三角形
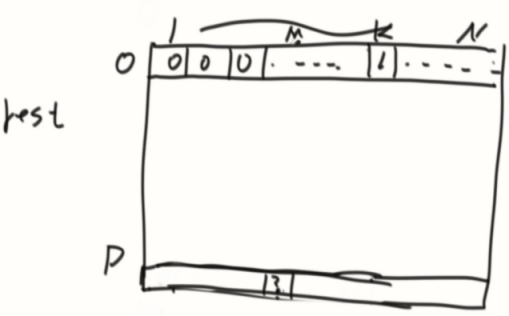
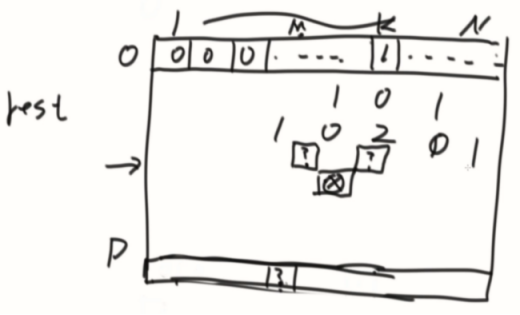
计算到最后一排,看落到M上的数是几就返回几。会撞墙的杨辉三角形(指的是在1和N的情况)

#include <iostream> #include <vector> using namespace std; //1.递归 int walk(const int &n,int cur_pos,int remain_step,const int &k) { if(n<1||cur_pos<1||cur_pos>n||remain_step<0||k<0||k>n) return 0; if(remain_step==0) return cur_pos==k?1:0; int count=0; if(cur_pos==1) count=walk(n,cur_pos+1,remain_step-1,k); else if(cur_pos==n) count=walk(n,cur_pos-1,remain_step-1,k); else count=walk(n,cur_pos+1,remain_step-1,k)+walk(n,cur_pos-1,remain_step-1,k); return count; } //2.动态规划 int walk1(const int& n, int cur_pos, int remain_step, const int& k) { vector<vector<int> > dp(remain_step+1,vector<int>(n+1,0)); dp.at(0).at(k)=1; for(int i=1;i<=remain_step;++i) { for(int j=1;j<=n;++j) { dp.at(i).at(j)+=j-1>=1?dp.at(i-1).at(j-1):0; dp.at(i).at(j)+=j+1>n?0:dp.at(i-1).at(j+1); } } return dp.at(remain_step).at(cur_pos); } int main() { cout<<walk(6,1,5,6)<<endl; cout<<walk1(6,1,5,6)<<endl; return 0; }