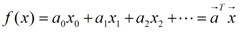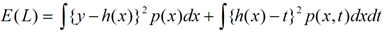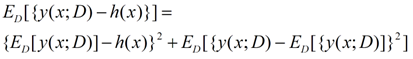数学解释
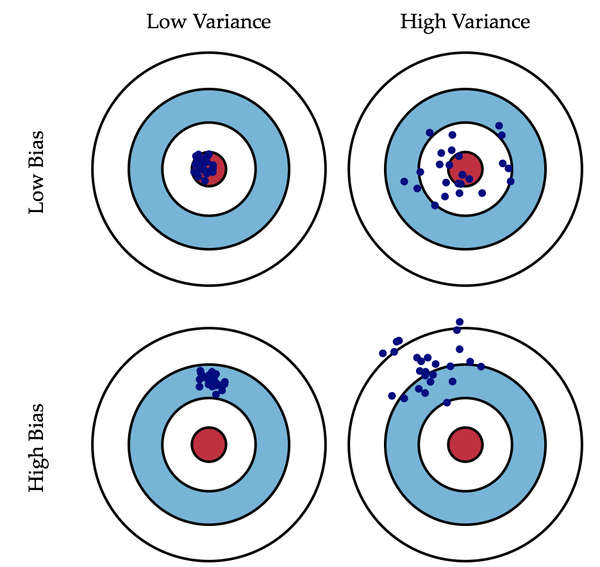
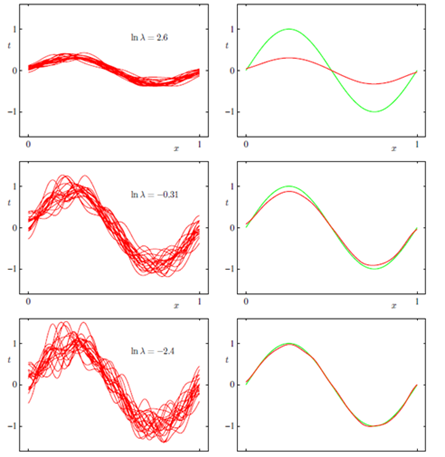
偏差:描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据,如下图第二行所示。
方差:描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散,如下图右列所示。
机器学习中的偏差和方差
首先,假设你知道训练集和测试集的关系。简单来讲是我们要在训练集上学习一个模型,然后拿到测试集去用,效果好不好要根据测试集的错误率来衡量。但很多时候,我们只能假设测试集和训练集的是符合同一个数据分布的,但却拿不到真正的测试数据。这时候怎么在只看到训练错误率的情况下,去衡量测试错误率呢?
由于训练样本很少(至少不足够多),所以通过训练集得到的模型,总不是真正正确的。(就算在训练集上正确率100%,也不能说明它刻画了真实的数据分布,要知道刻画真实的数据分布才是我们的目的,而不是只刻画训练集的有限的数据点)。而且,实际中,训练样本往往还有一定的噪音误差,所以如果太追求在训练集上的完美而采用一个很复杂的模型,会使得模型把训练集里面的误差都当成了真实的数据分布特征,从而得到错误的数据分布估计。这样的话,到了真正的测试集上就错的一塌糊涂了(这种现象叫过拟合)。但是也不能用太简单的模型,否则在数据分布比较复杂的时候,模型就不足以刻画数据分布了(体现为连在训练集上的错误率都很高,这种现象叫欠拟合)。过拟合表明采用的模型比真实的数据分布更复杂,而欠拟合表示采用的模型比真实的数据分布要简单。
在统计学习框架下,大家刻画模型复杂度的时候,有这么个观点,认为Error = Bias +Variance。这里的Error大概可以理解为模型的预测错误率,是有两部分组成的,一部分是由于模型太简单而带来的估计不准确的部分——偏差(Bias),另一部分是由于模型太复杂而带来的更大的变化空间和不确定性——方差(Variance)。
朴素贝叶斯的高偏差和低方差解释
有了上面的分析就容易分析朴素贝叶斯了。它简单的假设了各个数据之间是无关的,是一个被严重简化了的模型。所以,对于这样一个简单模型,大部分场合都会Bias部分大于Variance部分,也就是说高偏差而低方差。
在实际中,为了让Error尽量小,我们在选择模型的时候需要平衡Bias和Variance所占的比例,也就是平衡over-fitting和under-fitting。
偏差、方差如何权衡
偏差(bias)和方差(variance)是统计学的概念,首先得明确,方差是多个模型间的比较,而非对一个模型而言的,对于单独的一个模型,比如说:
这样的一个给定了具体系数的估计函数,是不能说f(x)的方差是多少。而偏差可以是单个数据集中的,也可以是多个数据集中的,这个得看具体的定义。
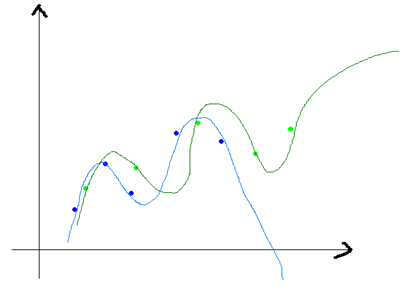
方差和偏差一般来说,是从同一个数据集中,用科学的采样方法得到几个不同的子数据集,用这些子数据集得到的模型,就可以谈他们的方差和偏差的情况了。方差和偏差的变化一般是和模型的复杂程度成正比的,就像本文一开始那四张小图片一样,当我们一味的追求模型精确匹配,则可能会导致同一组数据训练出不同的模型,它们之间的差异非常大。这就叫做方差,不过他们的偏差就很小了,如下图所示:
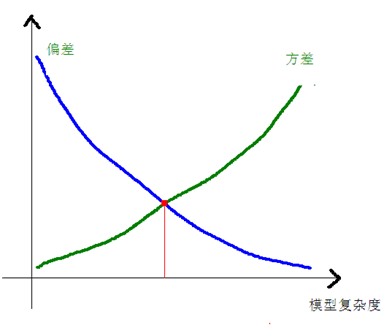
上图的蓝色和绿色的点是表示一个数据集中采样得到的不同的子数据集,我们有两个N次的曲线去拟合这些点集,则可以得到两条曲线(蓝色和深绿色),它们的差异就很大,但是他们本是由同一个数据集生成的,这个就是模型复杂造成的方差大。模型越复杂,偏差就越小,而模型越简单,偏差就越大,方差和偏差是按下面的方式进行变化的:
当方差和偏差加起来最优的点,就是我们最佳的模型复杂度。
最后还是用数学的语言来描述一下偏差和方差:
E(L)是损失函数,h(x)表示真实值的平均,第一部分是与y(模型的估计函数)有关的,这个部分是由于我们选择不同的估计函数(模型)带来的差异,而第二部分是与y无关的,这个部分可以认为是模型的固有噪声。
对于上面公式的第一部分,我们可以化成下面的形式:
前一半是表示偏差,而后一半表示方差,我们可以得出:损失函数=偏差^2+方差+固有噪音。
这是一个曲线拟合的问题,对同分布的不同的数据集进行了多次的曲线拟合,左边表示方差,右边表示偏差,绿色是真实值函数。ln lambda表示模型的复杂程度,这个值越小,表示模型的复杂程度越高,在第一行,大家的复杂度都很低的时候,方差是很小的,但是偏差同样很小,但是到了最后一幅图,我们可以得到,每个人的复杂程度都很高的情况下,不同的函数就有着天壤之别了,但是偏差就很小了。