大师级的文章,总是能够使你更接近于事物的本质。
最近看了pongba的数学之美番外篇:快排为什么那么快。文中提到了Mackay的一篇文章(这里是译文),里面提到了使用信息论来解释快排与堆排的速度差异的本质原因。看罢,内心有种莫名的激动。虽不懂信息论,但Mackay(大师毕竟是大师),最简单的解释,却直接触到了本质。有兴趣的可以看看Mackay的这篇文章。这里,只是我自己的一点感悟。
信息熵是什么?
一个事件,它的信息量大小和它的不确定性有直接的关系。比如说,我们要搞清楚一件非常非常不确定的事,或是我们一无所知的事情,就需要了解大量的信息。相反,如果我们对某件事已经有了较多的了解,我们不需要太多的信息就能把它搞清楚。所以,从这个角度,我们可以认为,信息量的度量就等于不确定性的多少。
我们把这个信息的度量叫做“熵”,熵越大表明这个事件的结果越难以预测,同时事件的发生将给我们带来越多的信息。
大家都掷过硬币。我们把掷(正常的)硬币这个事件的熵看做是1bit,为什么把一次比较的结果看成是1bit的信息呢?
可以这么解释:
一个抛硬币 正反各 1/2 概率。 如果信号源是这个, 所含有的信息量就是 - 1/2 * log (1/2) + -1/2 * log(1/2) = 1 bit 。
所以, 一个能生成 1/2、 1/2 概率(等概率)分布的信号所含的信息量就是 1bit 。比较就是这样的运算, 看作 cmp(a, b) 看作是抛硬币. 每次返回的是1个 bit。 有人会质疑,因为有时候要满足序的性质, 如 a>b, b>c 则 a>c 导致第三次问 cmp(a, c) 的时候不能以 1/2 1/2 的 概率生成随机信号. 其实, 一个好的排序算法就是避免使用了 cmp(a, b) cmp(b, c) 得到 a>b b>c 后还比较一次 a, c. 最佳的排序算法, 就是每次都能从 cmp 得到1bit 的信息。
但是,如果这个硬币被做过手脚,使得正面的概率大于反面的概率(或者反相反),那么这个事件的熵将<1bit。因为,我们对于结果的情况已经有所知道,显然,得到的信息也就少了。
更极端的情况,如果这个硬币是两个正面(或者相反),那么这个事件的熵将为0 bit,因为,我们完全知道结果是怎么样的。
1、排序与信息熵
为什么可以将信息论延伸到(基于比较的)排序?
熵是信息科学中的一个重要概念, 用来表示事物的不确定性. 排序就是使序列从无序到有序的过程, 无序就是不确定性, 因此可以用信息熵的概念来描述序列的无序程度,进而研究基于比较的排序算法的效率。
所以,想让基于比较的排序更快,等价于让每次比较的信息熵达到最大。所以,让每次比较的结果概率相等(使得每次比较的信息熵接近1bit),这是算法改进的核心思想。给出一个题目:有5个数,最少需要几次比较,来实现数据的排序?
设序列S 长度为n, 则该系列共有x = n!种不同的排列, 若将该序列看做信源的输出, 设每种排列出现的概率相同, 则根据离散随机变量的信息熵的定义, 序列S 的平均信息量, 即信息熵定义为:
Hn = l(x ) = log2(x ) =log2n! (bit)
5个整数,产生的全排列有 5!=120 种,从信息论的角度,信息量就是log2{120} = 6.90689059560852 bit,而两个数比较一次,最多可以产生1bit的信息量,所以7次比较几乎就是极限了。
当然这不是说你比较7次就可以得出排序结果的,而是当你尝试了无数次之后,发现,7次是它的极限次数。
下面,我们来看看,运用每次比较得到的信息熵接近于1bit的思想,来具体的实现,上诉的排序过程:
设原序列由(a, b, c, d , e ) 5 个元素组成,
首先分别对(a, b) 和(c, d ) 进行排序, 设排序结果分别为[a b ] 和[ c d ] ( [ x y ] 表示已排序) (对于其他排序结果, 以下分析过程相同) , 显然这一步需要2 次比较.
然后比较a 与c, 若a < c, 则排序结果为[a c d ], 用折半插入法经过2 次比较将e 插入到[ac d ] 当中,
最后将b 插入到已排序的序列, 由于已知b > a, 所以用折半插入法插入b, 最坏情况下只需要2 次比较. 若a > c, 排序结果为[ c a b ], 同样用折半插入法经2 次比较将e 插入, 由于c 已与d比较过, 因此最后将d 插入到已排序的序列最多也只需要2 次比较.
综上, 整个排序过程最多只需要7次比较. 第一步a 与b 及c 与d 的比较显然各减少1 bit 信息熵, 此时序列还有30 种不同的排列, 剩余的信息熵为4. 9069 b it. a 与c 比较后, 序列还剩15 种排列, 剩余的信息熵为3. 9069 b it, 所以这次比较也减少信息熵1 bit. 插入e 后, 若e < a, 序列可能出现3 种排列, 若e > a, 则有16 种可能的排列, 因此其平均信息熵为:
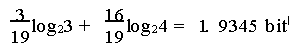
所以2 次比较减少信息熵1.9724 bit, 最后2 次比较减少1.9345 bit. 可见每次比较减少信息熵接近1 bit, 因此排序效率达到最高。
2、冒泡、选择、插入,为什么那么慢?
首先我们来看三种经典的平方复杂度算法。它们的效率并不高,原因就在于算法过程中会出现越来越多概率严重不均的比较。
1、冒泡
随着冒泡排序的进行,整个序列将变得越来越有序,位置颠倒的泡泡将越来越少;
2、选择排序
选择排序的每一趟选择中,你都会不断得到越来越大的数,同时在以后的比较中找到更大的数的概率也越来越低;
3、插入排序
在插入排序中,你总是把新的数与已经排好的数按从大到小的顺序依次进行比较,可以想到新的数一开始就比前面所有的数中最大的那个还大的概率是相当小的。受此启发,我们可以很自然地想到一个插入排序的改进:处理一个新的数时,为何不一开始就与前面处理过的数中的中位数进行比较?这种比较的熵显然更大,能获取的信息量要大得多,明显更有价值一些。这就是插入排序的二分查找改进。
3、快排为什么那么快?
快速排序算法中,比较的信息熵不会因为排序算法的进行而渐渐减小,这就是快速排序比上面几个排序算法更优秀的根本原因。
仔细回顾快速排序算法的过程,我们可以看出,每次比较的两种结果出现的概率完全由这一趟划分过程所选择的基准关键字决定:如果选择的基准关键字刚好是当前处理的数字集合的中位数,则比较结果的不确定性达到最大(一次比较的信息熵达到1bit)。这个时候,快排的比较次数,也就等于排序所需要的总信息熵:log2n! (bit) 这也正是快排的时间复杂度。
4、快排又为不那么快?
如果选择的基准关键字过大或过小,都会出现比较产生的结果不均等的情况,这使得每次比较平均带来的信息量大大减少。
比如:选择的主元为最小值,那么跟这个主元进行的比较得到的信息熵为0bit。因为,每次的结果都是肯定的。
看看主元随机时候的情况:
当主元随机选择的时候:我们不妨令轴元素为pivot,第一次比较结果是a1<pivot,那么可以证明第二次比较a2也小于pivot的可能性是2/3!这容易证明:如果a2>pivot的话,那么a1,a2,pivot这三个元素之间的关系就完全确定了——a1<pivot<a2,剩下来的元素排列的可能性我们不妨记为P(不需要具体算出来)。而如果a2<pivot呢?那么a1和a2的关系就仍然是不确定的,也就是说,这个分支里面含有两种情况:a1<a2<pivot,以及a2<a1<pivot。对于其中任一种情况,剩下的元素排列的可能性都是P,于是这个分支里面剩下的排列可能性就是2P。所以当a2<pivot的时候,还剩下2/3的可能性需要排查。
再进一步,如果第二步比较果真发现a2<pivot的话,第三步比较就更不妙了,模仿上面的推理,a3<pivot的概率将会是3/4!
这就是快排也不那么快的原因,它不能保证每次比较结果的概率都是相同的(1/2 :1/2),因此,每次比较的信息熵不是都=1bit。
如果你想改进快排,那么可以试试把精力放在提高每次比较的信息熵。