matlab练习程序（非线性常微分方程组参数拟合）

和线性常微分方程组参数拟合类似，我们要用差分代替微分，然后进行插值处理，然后构造最小化函数。

最后用最优化方法处理该函数即可。

这里举个例子，先随便设一个非线性微分方程组，并给定初值：

 

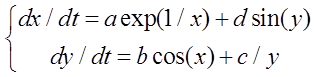
然后定义最小化函数：

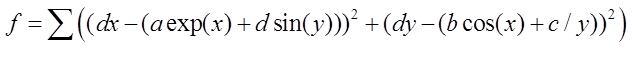
最后用之前介绍的非线性最优化方法解决。

matlab代码如下：

clear all;close all;clc;

bsrc = rand(4,1);
[t,h] = ode45(@(t,x)test1(t,x,bsrc),[0 100],[1 1]);
plot(t,h(:,1),'r');
hold on;
plot(t,h(:,2),'r');

hold on;
t = t(1:3:2*end/3);
x1 = h(1:3:2*end/3,1);
x2 = h(1:3:2*end/3,2);
plot(t,x1,'ro');
plot(t,x2,'ro');

T=min(t):0.1:max(t);        %插值处理，如果数据多，也可以不插值
X1=spline(t,x1,T)';
X2=spline(t,x2,T)';
plot(T,X1,'b.');
plot(T,X2,'b.');

dX1 = diff(X1)*10; dX1=[dX1;dX1(end)];
dX2 = diff(X2)*10; dX2=[dX2;dX2(end)];

%BFGS求解
syms k1 k2 k3 k4;
ff = sum((dX1 - (k1*exp(1./X1)+k4*sin(X2))).^2+(dX2-(cos(X1)*k2+k3*(1./X2))).^2);
dff1 = diff(ff,k1);dff2 = diff(ff,k2);
dff3 = diff(ff,k3);dff4 = diff(ff,k4);

f = inline(char(ff),'k1','k2','k3','k4');
g1 = inline(char(dff1),'k1','k2','k3','k4');
g2 = inline(char(dff2),'k1','k2','k3','k4');
g3 = inline(char(dff3),'k1','k2','k3','k4');
g4 = inline(char(dff4),'k1','k2','k3','k4');

b = rand(4,1);
rho=0.2;sigma=0.2;
H=eye(4);

re=[];
for i=1:1000
    g=[g1(b(1),b(2),b(3),b(4));
        g2(b(1),b(2),b(3),b(4));
        g3(b(1),b(2),b(3),b(4));
        g4(b(1),b(2),b(3),b(4));];
    
    dk=-inv(H)*g;
    mk=1;
    
    for j=1:50
        new=f(b(1)+rho^j*dk(1),...
            b(2)+rho^j*dk(2),...
            b(3)+rho^j*dk(3),...
            b(4)+rho^j*dk(4));
        
        old=f(b(1),b(2),b(3),b(4));
        if new < old +sigma*rho^j*g'*dk
            mk=j;
            break;
        end
    end
    
    norm(g)
    if norm(g)<1e-30 || isnan(new)
        break;
    end
    
    b = b + rho^mk*dk;
    gg=[g1(b(1),b(2),b(3),b(4));
        g2(b(1),b(2),b(3),b(4));
        g3(b(1),b(2),b(3),b(4));
        g4(b(1),b(2),b(3),b(4));];
    
    q = gg - g;             %q = g(k+1)-g(k)
    p = rho^mk*dk;          %p = x(k+1)-x(k)
    H = H - (H*p*p'*H)/(p'*H*p) + (q*q')/(q'*p);    %矩阵更新
    
end

bsrc
b

[t,h] = ode45(@(t,x)test1(t,x,b),[0 100],[1 1]);
plot(t,h(:,1),'g');
hold on;
plot(t,h(:,2),'g');

test1.m：

function dy=test1(t,x,A)
a = A(1);       
b = A(2);     
c = A(3);
d = A(4);
dy=[a*exp(1/x(1))+d*sin(x(2));
   cos(x(1))*b+c/x(2)];

结果如下：

上面这个结果还算可以。

不过由于是非线性微分方程组，参数差一点就可能导致系统后续差别越来越大，所谓混沌与蝴蝶效应。

所以大多数拟合的结果类似下面或更糟：

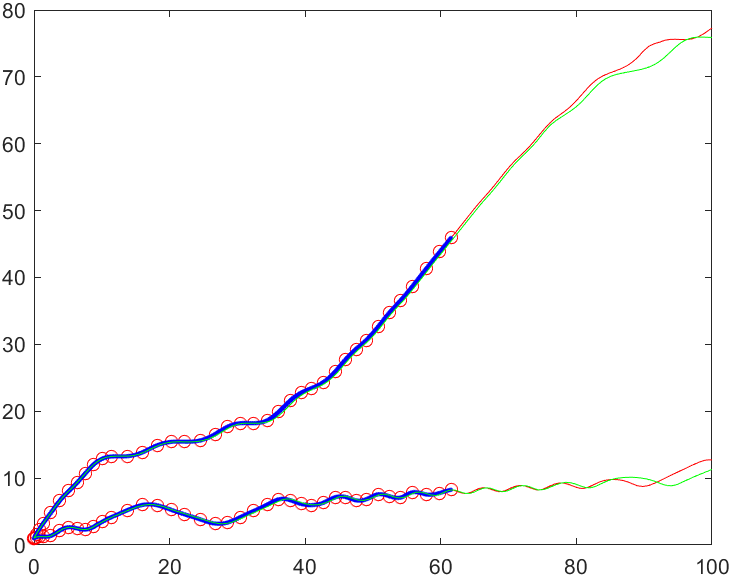
注：

　　后来我又看了一下，其实这里还是属于线性系数的，因为a,b,c,d四个系数并没在非线性函数中。

　　非线性系数我做了几次试验，效果不甚理想，后面有时间再写一篇。