有两个向量,我们想从起始向量平滑的过度到终止向量,那么中间的向量就可以通过插值的方式得到。
这在图形学中图形旋转或者机器人中物体姿态旋转都可以用到。
有三种方法:Lerp,NLerp和SLerp。
Lerp为线性插值,公式如下:

NLerp为线性插值后归一化,公式如下:
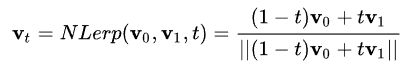
SLerp为球面插值,公式如下:
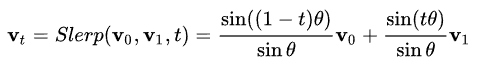
公式中的v0和v1就在起始与结束向量,换成四元数同理。
t为插值的中间值,球面插值中theta为两个向量间的夹角。
实现代码如下:
clear all; close all; clc; v1=[1 2 3]; %起始向量 v2=[4 -5 -6]; %终止向量 %转为单位向量 nv1 = v1/norm(v1); nv2 = v2/norm(v2); %画出起始终止向量 quiver3(0,0,0,nv1(1),nv1(2),nv1(3)); hold on; quiver3(0,0,0,nv2(1),nv2(2),nv2(3)); %起始终止向量转为四元数 x = nv1(1);y=nv1(2);z=nv1(3); q1 = angle2quat(x,y,z); x = nv2(1);y=nv2(2);z=nv2(3); q2 = angle2quat(x,y,z); %计算向量夹角 w = acos(sum(nv1.*nv2)); figure; %四元数插值 for t=0:0.1:1 q = sin((1-t)*w)/sin(w)*q1 + sin(t*w)/sin(w)*q2; %球面插值 slerp % q = (1-t)*q1 + t*q2; %一般插值 lerp % q = q/norm(q); %一般插值归一化 nlerp [x,y,z] = quat2angle(q); l=[x y z]; x = x/norm(l); y = y/norm(l); z = z/norm(l); quiver3(0,0,0,x,y,z); hold on; end figure; %向量插值 for t=0:0.1:1 q = sin((1-t)*w)/sin(w)*nv1 + sin(t*w)/sin(w)*nv2; %球面插值 slerp % q = (1-t)*nv1 + t*nv2; %一般插值 lerp % q = q/norm(q); %一般插值归一化 nlerp quiver3(0,0,0,q(1),q(2),q(3)); hold on; end
结果如下:
初始两个向量:
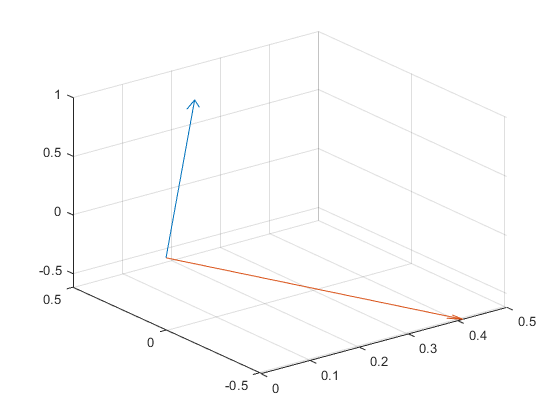
四元数球面插值:

向量球面插值:
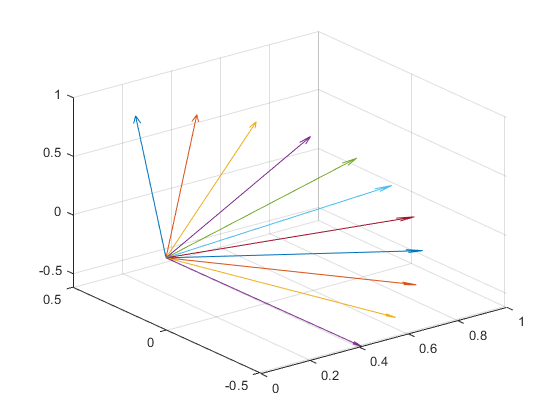
向量直接插值:
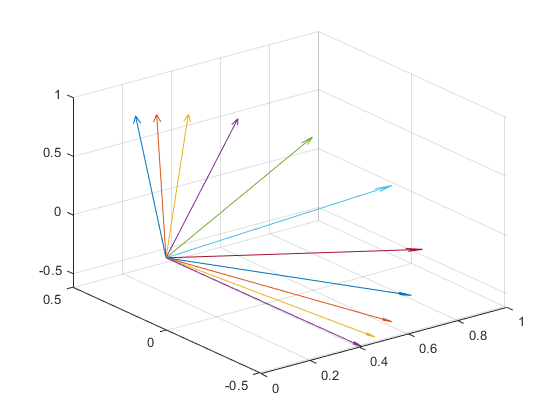
从效果上看,向量球面插值应该是最好的,向量直接插值在转动角较大的时候无法均匀插值。
网上很多插值都是通过四元数球面插值来做的,看结果并不是很均匀,可能是我这里用法不对?还请知道的人解释一下。