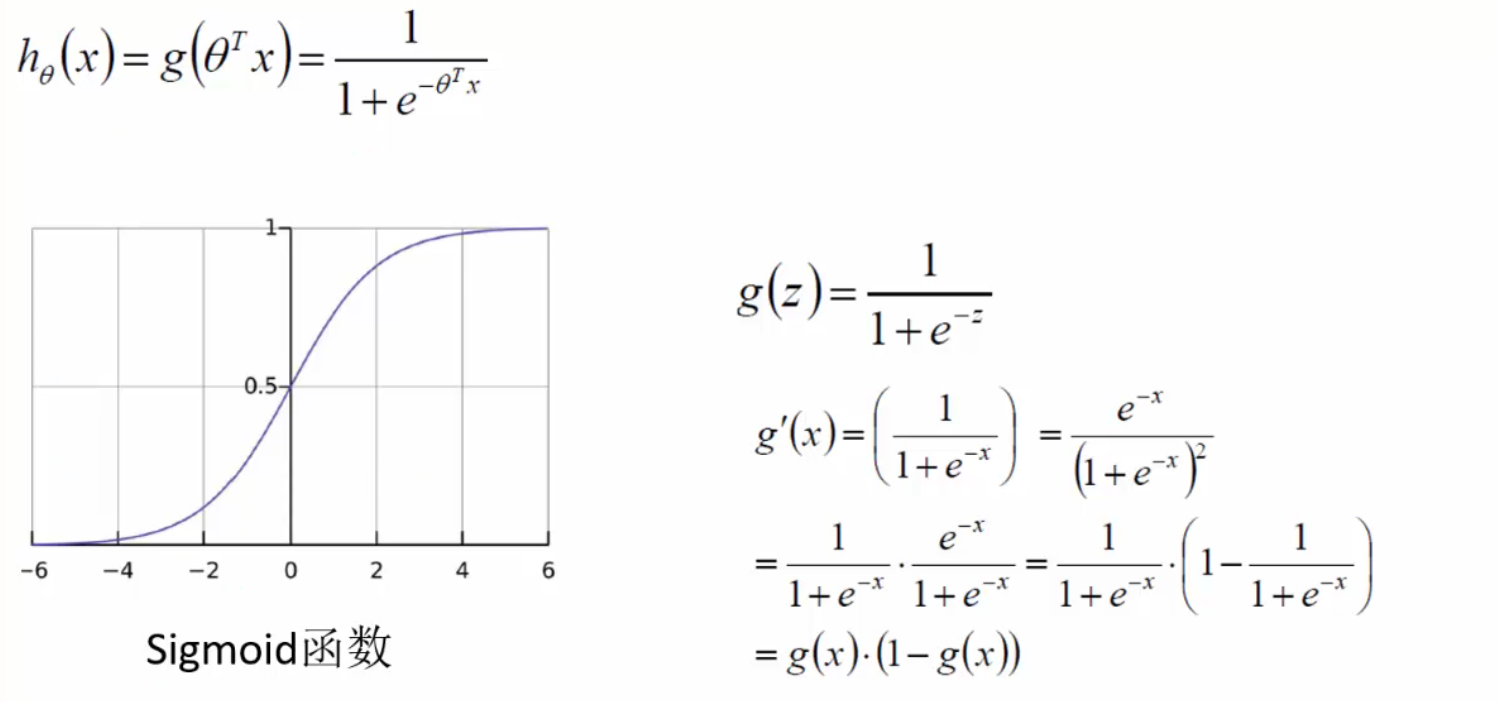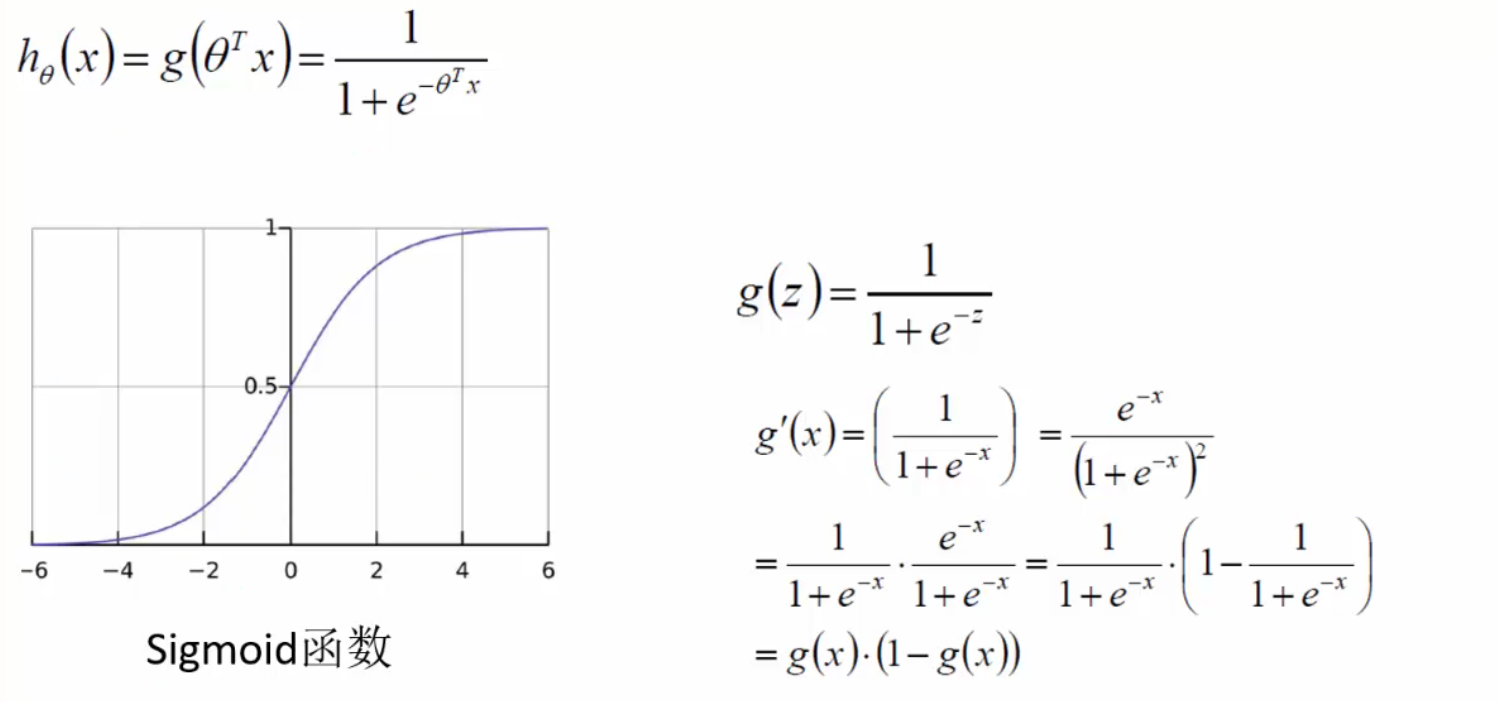[ML学习笔记] 回归分析(Regression Analysis)
回归分析:在一系列已知自变量与因变量之间相关关系的基础上,建立变量之间的回归方程,把回归方程作为算法模型,实现对新自变量得出因变量的关系。
回归与分类的区别:回归预测的是连续变量(数值),分类预测的是离散变量(类别)。
## 线性回归
线性回归通过大量的训练出一个与数据拟合效果最好的模型,实质就是求解出每个特征自变量的权值θ。
设有特征值x1、x2(二维),预测值 $ h_ heta(x)= heta_0 + heta_1x_1 + heta_2x_2 $。将其写为矩阵形式:令x0为全为1的向量,则预测值 $ h_ heta(x)=sum_{i=0}^n heta_i x_i = heta^T x$。
真实值和预测值之间的偏差用 (varepsilon) 表示,则有预测值 $ y^{(i)} = heta^Tx^{(i)} + varepsilon^{(i)}$。
假设误差(varepsilon^{(i)})是独立同分布的(通常认为服从均值为 (0) 方差为 (sigma^2) 的正态分布),有:
[�egin{split}
&p(epsilon^{(i)})=frac{1}{sqrt{2pi}sigma}e^{-dfrac{(epsilon^{(i)})^2}{2sigma^2}} \
代入则有&p(y^{(i)}mid x^{(i)}; heta)=frac{1}{sqrt{2pi}sigma}e^{-dfrac{( y^{(i)}- heta^Tx^{(i)} )^2}{2sigma^2}} \
end{split}
]
符号解释
p(x|theta)表示条件概率,是随机变量
p(x;theta)表示待估参数(固定的,只是当前未知),可直接认为是p(x),加了分号是为了说明这里有个theta参数
上式用语言描述就是,要取一个怎样的( heta),能够使得在(x^{(i)})的条件下最有可能取到(y^{(i)})。
可用极大似然估计求解,
[L( heta)=prod_{i=1}^mp(y^{(i)}mid x^{(i)}; heta)=prod_{i=1}^mfrac{1}{sqrt{2pi}sigma}e^{-dfrac{( y^{(i)}- heta^Tx^{(i)} )^2}{2sigma^2}}
]
[�egin{split}
l( heta)&=log L( heta)\
&=logprod_{i=1}^mfrac{1}{sqrt{2pi}sigma}e^{-dfrac{( y^{(i)}- heta^Tx^{(i)} )^2}{2sigma^2}} \
&= sum_{i=1}^mlogfrac{1}{sqrt{2pi}sigma}e^{-dfrac{( y^{(i)}- heta^Tx^{(i)} )^2}{2sigma^2}} \
&= mlogfrac{1}{sqrt{2pi}sigma}-frac{1}{2sigma^2}sum_{i=1}^m(y^{(i)}- heta^Tx^{(i)})^2\
end{split}
]
化为求目标函数(J( heta)=dfrac{1}{2}sum_{i=1}^m(h_ heta(x^{(i)})-y^{i})^2)的最小值。
###最小二乘法求解
用矩阵形式表示:
[J( heta)=frac{1}{2}sum_{i=1}^m(h_ heta(x^{(i)})-y^{i})^2
=frac{1}{2}(X heta-y)^T(X heta-y)
]
然后对( heta)求导:
[�egin{split}
riangledown_ heta J( heta)&= riangledown_ heta(frac{1}{2}(X heta-y)^T(X heta-y))\
&= riangledown_ heta(frac{1}{2}( heta^TX^T-y^T)(X heta-y))\
&= riangledown_ heta(frac{1}{2}( heta^TX^TX heta- heta^TX^Ty-y^TX heta+y^Ty))\
&=frac{1}{2}(2X^TX heta-X^Ty-(y^TX)^T)\
&=X^TX heta-X^Ty
end{split}
]
令 (X^TX heta-X^Ty=0),则有最终结果 ( heta = (X^TX)^{-1}X^Ty)
### 梯度下降法求解
上述方法有时候会出现不能直接求出极值的情况,比如矩阵不可逆,只能通过不断优化的过程求解。梯度下降顾名思义,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度,然后朝着梯度相反的方向,就能让函数值下降的最快。
设 (h_ heta(x)= heta_1x+ heta_0),
[�egin{split}
J( heta_0, heta_1)&=frac{1}{2m}sum_{i=1}^m(h_ heta(x^{(i)})-y^{i})^2\
frac{partial J( heta_0, heta_1)}{partial heta_0} &= frac{1}{m}sum_{i=1}^m(h_ heta(x^{(i)})-y^{i})\
frac{partial J( heta_0, heta_1)}{partial heta_1} &= frac{1}{m}sum_{i=1}^m(h_ heta(x^{(i)})-y^{i})x_i\
end{split}
]
更新后的( heta_0, heta_1)(选取合适的(alpha)做步长):
[�egin{split}
heta_0:= heta_0-alpha*frac{partial J( heta_0, heta_1)}{partial heta_0}\
heta_1:= heta_1-alpha*frac{partial J( heta_0, heta_1)}{partial heta_1}
end{split}
]
## 逻辑回归(二分类问题)
逻辑回归本质不是回归,而是分类。可用Sigmoid函数 (g(x) = dfrac{1}{1+e^{-x}})将任意实数x映射到(0,1)区间从而进行类别划分,一般默认概率大于等于0.5则为1,小于0.5则为0,也可以自行设置阈值。
用一句话来说就是:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数得出分类概率,通过阈值过滤来达到将数据二分类的目的。