Question
Q1.Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.
Example:
Input: 1->2->4, 1->3->4 Output: 1->1->2->3->4->4
Q2.Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.
Example:
Input: [ 1->4->5, 1->3->4, 2->6 ] Output: 1->1->2->3->4->4->5->6
在解决将k个已排序(从小到大)好的链表合并成一个已排序(从小到大)的链表前,我们先从一个特例开始,即将两个链表合并成一个。
Answer
1.合并两个排列好的链表
问题就是将两个已排序的链表合并成一个,这是归并排序里的一个基本操作。
现在描述以下解决这个问题的算法,用数组来描述。
我们输入两个数组,设为A,B,输出输出C,加入三个计数器Aptr,Bptr,Cptr,初始化为数组开头。
取A[Aptr]和B[Bptr]的较小值拷贝到C的下一个位置,相应的计数器加一,重复该操作,直到某个计数器指向的索引值大于数组的边界。
这时候代表一个数组的元素已经全部拷贝到C的相应位置了,我们将另一个数组剩下的元素拷贝到C里。
回到Leetccode的这个问题,从链表的角度,计数器和链表元素可以用指针来代替,输入和输出数组也可以通过链表头指针访问,下面通过不完整的代码实现这个算法的思想。
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// first_Node用来输出链表, last_Node用作上面算法描述的计数器(即Cptr),也用作插入元素,代表输出C的最后一个节点 ListNode *first_Node = NULL, *last_Node = NULL;
// 在两个数组都没被拷贝到C时的操作。 while (l1 != NULL && l2 != NULL) {
// 判断A[Aptr](与l1->val一致),B[Bptr](与l2->val一致)哪个较小,将较小的插入到链表C的最后,Aptr和Bptr相应加一(相当于l1,l2)
if (l1->val > l2->val) { last_Node->next = l2; last_Node = last_Node->next; l2 = l2->next; } else { last_Node->next = l1; last_Node = last_Node->next; l1 = l1->next; } }
// 将剩下的元素插入到C的最后 if (l1 == NULL && l2 != NULL) { last_Node->next = l2; } else if (l1 != NULL && l2 == NULL) { last_Node->next = l1; }
// 返回链表C return first_Node; }
上面的代码已经很能体现代码的具体思想了,剩下的工作就是将代码完善,将边界的情况考虑周全,实际呢,这又是特别麻烦的,一个不小心就会出现问题,比如说访问空指针。我们仔细考虑就会知道,上面代码没有对first_Node进行初始化,所以我们需要对first_Node判断是否为空,空就要初始化为对应的节点。那么在哪里判断呢,很容易想到,我们需要在判断A[Aptr]和B[Bptr]哪个较小后加入,然而这还没结束,将剩下的元素插入到C的最后 后的代码也没有对first_Node(last_Node)是否为空作判断,可又有对last_Node进行操作,这是十分危险的,所以我们也要在这里加入判断。最后完整的代码如下:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { ListNode *first_Node = NULL, *last_Node = NULL; while (l1 != NULL && l2 != NULL) { if (l1->val > l2->val) { if (first_Node == NULL) { first_Node = l2; last_Node = first_Node; } else { last_Node->next = l2; last_Node = last_Node->next; } l2 = l2->next; } else { if (first_Node == NULL) { first_Node = l1; last_Node = first_Node; } else { last_Node->next = l1; last_Node = last_Node->next; } l1 = l1->next; } } if (l1 == NULL && l2 != NULL) { if (first_Node == NULL) first_Node = l2; else last_Node->next = l2; } else if (l1 != NULL && l2 == NULL) { if (first_Node == NULL) first_Node = l1; else last_Node->next = l1; } return first_Node; }
2.合并k个排列好的链表
好了,有了上面的例子,我们合并k的链表也会有思路了,模仿上面算法的思路,我们可以每次将k个链表的最小值比较一遍,取最小值,将其拷贝到输出链表C中,当然这是可行的,时间复杂度为O(kN),N为最后剩下链表的长度,想了想感觉这有点麻烦,所以我们不妨考虑另一种方法。
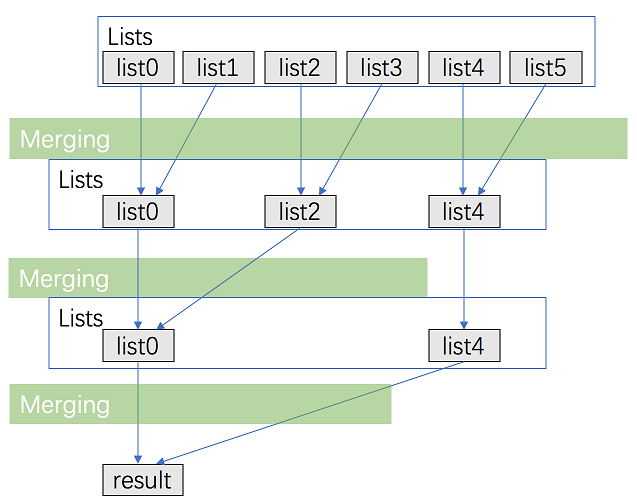
按照上一题的思路,其实我们可以两两链表合并,最后合并成一个链表,这样我们就可以重用上面的代码了。两两合并可以是链表1和链表2合并后的链表 再和链表3合并,以此类推,也可以是链表1和链表2合并为链表①,链表3和链表4合并为链表②,依次类推,①又和②合并……,如下图所示。聪明的你一比较就知道后者的效率会高很多,因为合并的次数明显变少了。因此,我们根据后者编写代码:
ListNode* mergeKLists(vector<ListNode*>& lists) {
// 递归终止的条件 if (lists.size() == 0) return NULL; if (lists.size() == 1) return lists[0]; // 返回链表头节点指针
vector<ListNode*> tmpVec;
// 每两个链表合并 for (int i = 0; i < lists.size()/2*2; i += 2) tmpVec.push_back(mergeTwoLists(lists[i], lists[i+1])); // 如果k为奇数,将剩下的最后一个加入到tmpVec中 if (lists.size()%2 != 0) tmpVec.push_back(lists[lists.size()-1]);
// 继续合并 return mergeKLists(tmpVec); }
实际上,这样的解决办法称为分治(divide and conquer),将一个大问题分为几个子问题来解决,在编程里经常用递归实现,上面就有所体现。