【题目描述】
随着智能手机的日益普及,人们对无线网的需求日益增大。某城市决定对城市内的公共场所覆盖无线网。
假设该城市的布局为由严格平行的129 条东西向街道和129 条南北向街道所形成的网格状,并且相邻的平行街道之间的距离都是恒定值 1 。东西向街道从北到南依次编号为0,1,2…128 , 南北向街道从西到东依次编号为0,1,2…128 。
东西向街道和南北向街道相交形成路口,规定编号为x 的南北向街道和编号为y 的东西向街道形成的路口的坐标是(x , y )。 在 某 些 路口存在一定数量的公共场所 。
由于政府财政问题,只能安装一个大型无线网络发射器。该无线网络发射器的传播范围
一个以该点为中心,边长为2*d 的正方形。传播范围包括正方形边界。
例如下图是一个d = 1 的无线网络发射器的覆盖范围示意图。
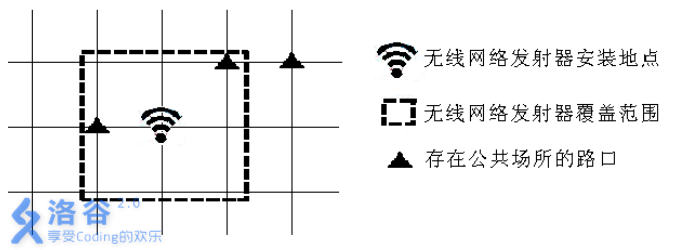
现在政府有关部门准备安装一个传播参数为d 的无线网络发射器,希望你帮助他们在城市内找出合适的安装地点,使得覆盖的公共场所最多。
【输入输出格式】
输入格式:输入文件名为wireless.in。
第一行包含一个整数d ,表示无线网络发射器的传播距离。
第二行包含一个整数n ,表示有公共场所的路口数目。
接下来n 行,每行给出三个整数x , y , k , 中间用一个空格隔开,分别代表路口的坐标( x , y )
以及该路口公共场所的数量。同一坐标只会给出一次。
输出格式:输出文件名为wireless.out 。
输出一行,包含两个整数,用一个空格隔开,分别表示能覆盖最多公共场所的安装地点 方案数,以及能覆盖的最多公共场所的数量
【输入输出样例】
1 2 4 4 10 6 6 20
1 30
对于100%的数据,1≤d≤20,1≤n≤20, 0≤x≤128,0≤y≤128,0<k≤1,000,000。

#include<iostream> using namespace std; int a[130][130]; struct Node { int mxv,cnt; } ans; int d,n,x_,y_; int find(int x,int y) { int u=0; for(int i=max(0,x-d); i<=min(x_,x+d); i++) for(int j=max(0,y-d); j<=min(y_,y+d); j++) u+=a[i][j]; return u; } int main() { cin>>d>>n; int x,y,v; for(int i=1; i<=n; i++) { cin>>x>>y>>v; a[x][y]=v; x_=max(x,x_),y_=max(y,y_); } for(int i=0; i<=x_; i++) { for(int j=0; j<=y_; j++) { int w=find(i,j); if(w>ans.mxv) { ans.mxv=w,ans.cnt=1; continue; } if(w<ans.mxv)continue; if(w==ans.mxv) { ans.cnt++; continue; } } } cout<<ans.cnt<<' '<<ans.mxv; }
【题目描述】
在有向图G 中,每条边的长度均为1 ,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
1 .路径上的所有点的出边所指向的点都直接或间接与终点连通。
2 .在满足条件1 的情况下使路径最短。
注意:图G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
【输入输出格式】
输入格式:输入文件名为road .in。
第一行有两个用一个空格隔开的整数n 和m ,表示图有n 个点和m 条边。
接下来的m 行每行2 个整数x 、y ,之间用一个空格隔开,表示有一条边从点x 指向点y 。
最后一行有两个用一个空格隔开的整数s 、t ,表示起点为s ,终点为t 。
输出格式:输出文件名为road .out 。
输出只有一行,包含一个整数,表示满足题目᧿述的最短路径的长度。如果这样的路径不存在,输出- 1 。
【输入输出样例】
3 2 1 2 2 1 1 3
-1
6 6 1 2 1 3 2 6 2 5 4 5 3 4 1 5
3
解释1:
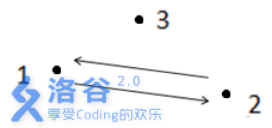
如上图所示,箭头表示有向道路,圆点表示城市。起点1 与终点3 不连通,所以满足题
目᧿述的路径不存在,故输出- 1 。
解释2:
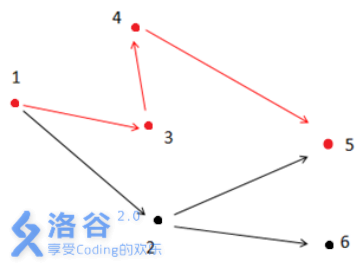
如上图所示,满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中,因为点2连了一条边到点6 ,而点6 不与终点5 连通。
对于30%的数据,0<n≤10,0<m≤20;
对于60%的数据,0<n≤100,0<m≤2000;
对于100%的数据,0<n≤10,000,0<m≤200,000,0<x,y,s,t≤n,x≠t。

#include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<iostream> #include<vector> using namespace std; int x,y,s,t,n,m,h[10002],f[10002],tr; vector<int>a[10002],b[10002]; void dfs(int u) { if (h[u])return; f[u]=1; h[u]=1; for (int i=0; i<b[u].size(); i++) dfs(b[u][i]); } void bfs(int u) { int g[10002],ans[10002],l=0,fl[10002],xx; memset(fl,0,sizeof(fl)); memset(ans,0,sizeof(ans)); for (int i=0; i<a[u].size(); i++) if (!fl[a[u][i]] && f[a[u][i]]) { ans[l]=1; g[l++]=a[u][i]; fl[a[u][i]]=1; } for (int i=0; i<l; i++) { if (g[i]==t) { tr=1; printf("%d",ans[i]); break; } xx=g[i]; for (int j=0; j<a[xx].size(); j++) if (!fl[a[xx][j]] && f[a[xx][j]]) { ans[l]=ans[i]+1; g[l++]=a[xx][j]; fl[a[xx][j]]=1; } } } int main() { scanf("%d%d",&n,&m); for (int i=0; i<m; i++) { scanf("%d%d",&x,&y); a[x].push_back(y); b[y].push_back(x); } scanf("%d%d",&s,&t); dfs(t); memset(h,0,sizeof(h)); for (int i=1; i<=n; i++) { if (!f[i])continue; for (int j=0; j<a[i].size(); j++) if (!f[a[i][j]]) { h[i]=1; break; } } for (int i=1; i<=n; i++) if (h[i])f[i]=0; if (f[s])bfs(s); if (!tr)printf("-1"); return 0; }
【题目描述】
已知多项式方程:
a0+a1x+a2x^2+..+anx^n=0
求这个方程在[1, m ] 内的整数解(n 和m 均为正整数)
【输入输出格式】
输入格式:输入文件名为equation .in。
输入共n + 2 行。
第一行包含2 个整数n 、m ,每两个整数之间用一个空格隔开。
接下来的n+1 行每行包含一个整数,依次为a0,a1,a2..an
输出格式:输出文件名为equation .out 。
第一行输出方程在[1, m ] 内的整数解的个数。
接下来每行一个整数,按照从小到大的顺序依次输出方程在[1, m ] 内的一个整数解。
【输入输出样例】
2 10 1 -2 1
1 1
2 10 2 -3 1
2 1 2
2 10 1 3 2
0
对于30%的数据:0<n<=2,|ai|<=100,an!=0,m<100
对于50%的数据:0<n<=100,|ai|<=10^100,an!=0,m<100
对于70%的数据:0<n<=100,|ai|<=10^10000,an!=0,m<10000
对于100%的数据:0<n<=100,|ai|<=10^10000,an!=0,m<1000000

#include<iostream> #include<cstdio> #include<cmath> using namespace std; int n,m,a[110],cnt,ans[1000010]; bool check(int x){ long long k=0; for(int i=0;i<=n;i++)k+=a[i]*pow(x,i); if(k==0)return 1; else return 0; } int main(){ scanf("%d%d",&n,&m); for(int i=0;i<=n;i++)scanf("%d",&a[i]); for(int i=1;i<=m;i++){ if(check(i)) ans[++cnt]=i; } printf("%d ",cnt); for(int i=1;i<=cnt;i++)printf("%d ",ans[i]); }

/* 0模任何数都等于0 考虑方程在剩余系意义下的解 选取质数p 若左边%p=0,则x是方程的解 但可能存在左边是p的倍数的情况, 所以选2个质数,不放心的话可以在多选几个 如何处理读入的高精度? 将系数以类似于读入优化的方式,边读入,边%p */ #include<cstdio> #include<cstring> using namespace std; int n,m,len,tot; char s[10010]; long long a[3][101],p[3],tmp,w; bool anti; bool b[1000001]; void turn(int k) { len=strlen(s); int j,g; if(s[0]=='-') {anti=true;g=1;} else {anti=false;g=0;} for(int i=1;i<=2;i++) { j=g; for(; j<len; j++) a[i][k]=(a[i][k]*10%p[i]+s[j]-'0')%p[i]; if(anti) a[i][k]=p[i]-a[i][k]; } } bool check(int x,int k) { tmp=0; w=1; for(int i=0; i<=n; i++) { tmp=(tmp+a[k][i]*w%p[k])%p[k]; w=w*x%p[k]; } return tmp; } int main() { p[1]=22861; p[2]=1000007977; scanf("%d%d",&n,&m); for(int i=0; i<=n; i++) { scanf("%s",s); turn(i); } for(int i=1; i<=p[1]; i++) { if(check(i,1)) continue; for(int j=i; j<=m; j+=p[1]) if(!check(j,2)) b[j]=true,tot++; } printf("%d ",tot); for(int i=1; i<=m; i++) if(b[i]) printf("%d ",i); }
