P1962 斐波那契数列

题面是这样的，其实斐波那契我们之前也有接触过，并不是什么太陌生的玩意，第一个想到的方法其实是用递归来做，这样的话其实是非常轻松的，but同志们你们有没有关注过这样一个鬼东西

你以为蓝题是让你切着玩的吗？？？？？？

果不其然，递归写了一个，大红大紫啊喂

（雾

不过的确过不了就是了，直到我打开了题解，发现了一个叫矩阵快速幂的玩意

Fn表示数列的第n项

那么我们如果把Fn，Fn-1写成蒟阵的形式，可以按照如下推导过程对这个蒟阵进行拆分，从而写成便于计算的形式

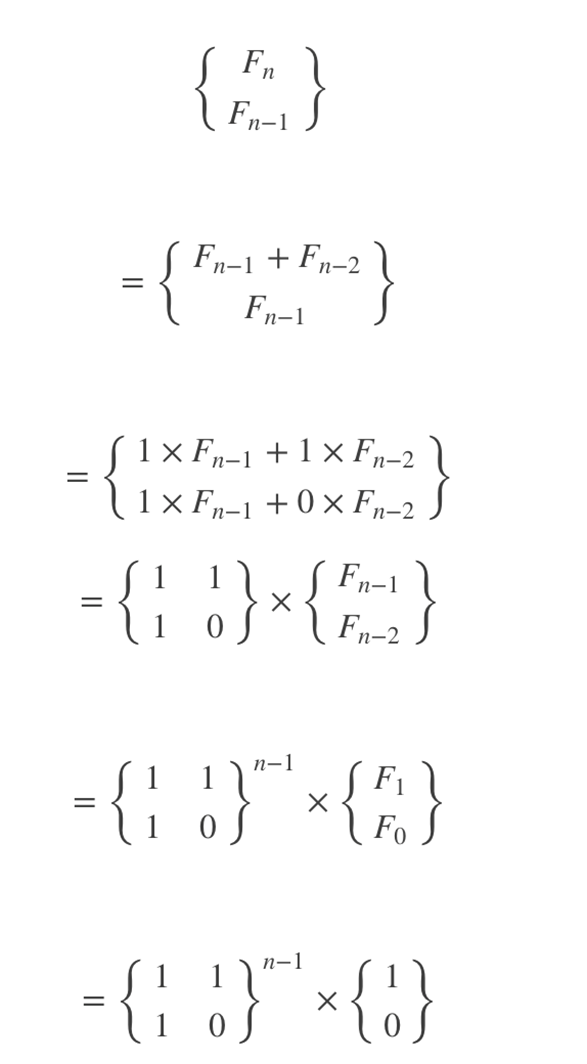
其实我们就是把递归用矩阵的方式写了出来，然后想求第n项就直接输出矩阵的n次幂即可

快速幂在另一篇博客里看这里qaq

其实这道题的难点就是矩阵快速幂，既然会了这个的话就没什么大问题啦~

代码如下：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-1);
#define rep(i,a,n) for(ll i=a;i<=n;i++) 
#define per(i,n,a) for(ll i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-9;
ll pp=1000000007;
ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;}
ll read(){
    ll ans=0;
    char last=' ',ch=getchar();
    while(ch<'0' || ch>'9')last=ch,ch=getchar();
    while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
//head   从这里开始哦 
struct matrix{
    ll a[2][2];
};//注意这里要用ll保证不会爆 
matrix operator *(matrix a, matrix b){//定义*运算 
    matrix c;
    rep(i,0,1)//简写的方式，for（int i =1;i<=n;++i)        
　　 rep(j,0,1){
            c.a[i][j]=0;
            rep(k,0,1)
                c.a[i][j] = (c.a[i][j]+a.a[i][k]*b.a[k][j])%pp;
        }
    return c;
}
ll k;
int main(){
    cin>>k;
    matrix a; 
    a.a[0][0]=0;a.a[0][1]=1;
    a.a[1][0]=1;a.a[1][1]=1; 
    matrix ans;
    ans.a[0][0]=1;ans.a[0][1]=0;
    ans.a[1][0]=0;ans.a[1][1]=1;//把ans初始化为单位矩阵 
    ll b=k-1;
    while(b){
        if(b&1)ans=ans*a;
        a=a*a;
        b/=2;
    }//一个快速幂 
    ll fk = (ans.a[0][0]+ ans.a[0][1])%pp;
    cout<<fk<<endl;//O(log B *2^3)
}