算数基本定理:
1.整数及其相关

2.唯一分解定理
对于任意的大于1的正整数N,N一定能够分解成有限个质数的乘积,即
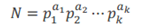
其中P1<P2<...<Pk,a1,a2,...,ak>=1;
证:
存在性:
若存在最小的N不满足条件,当N为质数是,显然不成立;当N为合数时,存在P,使得N=P*(N/P),N/P<N,与假设N为最小的矛盾,故一定存在;
即:假设N为最小的
当N为质数直接gg
当N为合数还是gg
故不存在...
唯一性:
假设N的分解不唯一
设存在最小的N,使得N=p1r1 p2r2 .... pkrk且N=q1t1 q2t2 .....qntn
则p1|q1t1 q2t2 .....qntn
假设p1=q1,且r1>=t1,那么两个式子同时除以p1t1,
有p1r1-t1.....=q10 .....
而经过变换后的式子要小于原式
这与假设N为最小的不满足的矛盾
(A是一个<=n的正整数 两个条件至少有一个成立)
素数的判定
下面来讲点OI的东西
这是一个现有的最快的确定性的判断质数的方法
其实就是弱智筛啊
还有另外一种不是百分百的算法,但是更快
Miller-rabin素性测试
如果n为素数,取a<n,设n-1=d*2r,则要么ad≡1(mod n)要么存在0<=i<r,使得ad*2^t≡-1(mod n),要么存在0<=i<r,使得ad*2^t≡-1(mod n)(有可能都满足)
对于任意一个a,如果满足这两个条件,n有可能是质数,但a如果不满足这两个条件中的任何一个,它一定不是质数。找k个a,如果都满足这两个条件,k-1个“更”有可能是质数
在选取k的时候,最好选取2,3,5,7,13,29,37,89至少保证int范围内不会出错
因为筛法的不确定性来自于随机的a,但是当选取的数足够好,就没有问题;
如果n是素数,取a<n,舍n-1=d*2r,则要么ad≡1(mod n),要么存在0<=i<r,使得a
部分代码:
int gg[8]={2,3,5,7,13,29,37,89}; long long kuaisumi(long long a,long long b1,long long c) { long long i=a; while(b1) { if(b1&1) { s=(s*i)%c; } i=(i*i)%c; b1>>=1; } return s%c; } bool miller_rabin(int a,int n) { int d=n-1,r=0; while(d%2==0) d/=2,r++; int x=kuaisumi(a,d,n); if(x==1)return true; for(int i=0;i<r;i++) { if(x==n-1)return true ; x=(long long )x*x%n; } return false;//可以对照素性测试看 } bool is_prime (int n) { if(n<=1)return false ; for(int a=0;a<8;a++) if(n==gg[a])return true;//一个个试 for(int a=0;a<8;a++) if(!miller_rabin(gg[a],n))return false; return true; }
最大公因数和最小公倍数
3,最大公因数
Gcd(a,b)=max{x(x|a,x|b)}
欧几里得算法的核心思想
gcd(a,b)=gcd(b,a-b)==>gcd(a,b)=gcd(b,a%b)
现在证明gcd(a,b)=gcd(b,a-b)
d=gcd(a,b) =>a=dx b=dy;
a-b=d(x-y);
“任意”:∀;“存在”:∃
对于gcd(b,a-b),∃ t>1,t|y,t|x-y;
t>1,t|y,t|x-y =>t|x,t|y =>td|a td|b
裴蜀定理
给定a,b,c,则ax+by=c有整数解的充要条件是gcd(a,b)|c
来证一下
不妨使用唯一分解定理
充分性:
d=gcd(a,b),
则d|a,d|b==>d|ax+by=c==>d|c充分性证毕
必要性:
设d=gcd(a,b),s=min(ax+by),s>0
a/s=q......r(0<=r<s)==>r=a-qs=a-q(ax+by)=(1-qx)a-qyb
因为s=min(ax+by),所以r=0==>s|a&&s|b==>
1-------s|gcd(a,b)
s=ax+by=b(nd)+y(md)==>
2-------d|s
综合1,2,得到s=d
证毕
一个应用
请证明:设p为质数,若p|ab,则p|a或p|b
证:
当p|a时,显然成立
否则,gcd(p,a)=1==>xp+ya=1
b=b*1=b(xp+ya)=pxb+yab
p|pxb==>p|yab
在做了这么多铺垫之后,我们终于要开始学习同余的有关知识了,
扩展欧几里得(辗转相除法)
目的:求ax+by=gcd(a,b)的一组解(x,y)
递归求解即可
int Exgcd(int a, int b, int &x, int &y) { if (!b) { x = 1; y = 0; return a; } int d = Exgcd(b, a % b, x, y); int t = x; x = y; y = t - (a / b) * y; return d; }
注意:
每一次返回的是三个值,x,y用取地址符
中国剩余定理

Ans=所有逆元加起来%P
这是一个特殊情况

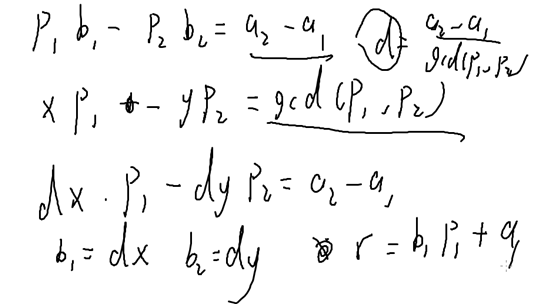
当有k个方程式的时候,就可以按照这个方法来两两合并
以上是正常做法,下面是长者的神奇方法
大数翻倍法
其实就是小学学习的求最小公倍数的方法,让较大的数遍历1~n进行乘法运算,直到较大数和较小数有最小公倍数时有解
这个方法解数学的时候还行,但是OI不好用
逆元及其相关
1.欧拉定理
设x1,x2,.....,xk,k=φ(n)为1~n中k个与n互质的数
结论一:axi与axj不同余
结论二:gcd(axi,n)=1
结论三:x1,x2,...,xk和ax1,ax2,...,axk一一对应
结论四:aφ(n)≡1(mod n)
计算:φ(m)=m*(1-1/p1)*......*(1-1/pi)
Back to here
请证明:如果n为素数,取a<n,设n-1=d*2r,则要么ad≡1(mod n)要么存在0<=i<r,使得ad*2^t≡-1(mod n),要么存在0<=i<r,使得ad*2^t≡-1(mod n)
证:由费马小定理得an-1≡1(mod n),已知n-1=d*2r
∴ad*2^r≡1(mod n)
∴ad*2^r-1≡0(mod n)
由平方差公式知:(ad*2^(r-1))(ad*2^(r-1))≡0(mod n)
∴原式=(ad-1)(ad+1)(ad*2+1)(ad*2^2).......(ad*2^(r-1)+1≡0(mod n)
2.线性求逆元
求1~n所有数 对p的逆元(p为质数)
为了减少时间,我们要尽量利用已经求出来的逆元进行计算,也就是说,当求i的逆元时,1~i-1的逆元已经求完了
设1<=i<=n
∵p/i=k......r
∴p=ik+r
ik+r≡0 (mod p)
kr-1+i-1≡0 (mod p)
i-1≡-kr-1 (mod p)
下面是证明

3.BSGS算法(baby-step gaint-step)但是我还是觉得北上广深更好
一道非常BT的题目
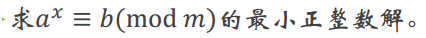
首先我们想到枚举,从1~phi(m)枚举即可得解,
所谓BSGS其实就是对暴力进行一个优化
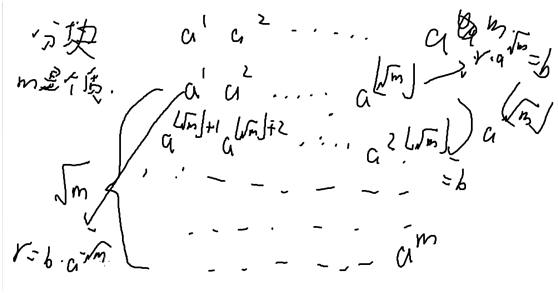
先暴力出第一行的sqrt(m)个数
然后从第二行找答案等价于第一行里面是否存在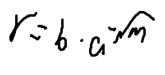
再从第三行找答案等价于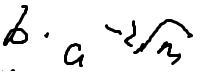
这样每一行就都能求解了
代码实现
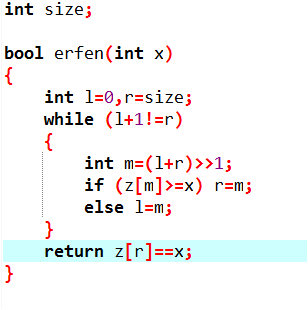
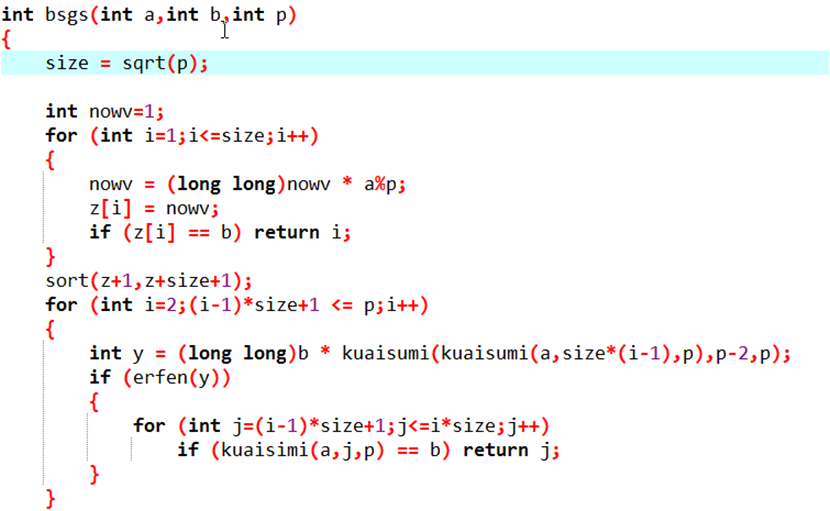
i-1行*size个数+1
数论函数:喂正整数吐整数

积性函数
积性函数:当gcd(a,b)=1时,ƒ(ab)=ƒ(a)ƒ(b)
完全积性函数:ƒ(ab)=f(a)f(b)
积性函数包括:
不变函数:ƒ(n)=n
欧拉函数:ƒ(n)=φ(n)
莫比乌斯函数:ƒ(n)=μ(n)
因子数目总数:ƒ(n)=d(n)
因子之和函数:ƒ(n)=σ(n)
证一下phi(ab)=phi(a)*phi(b);
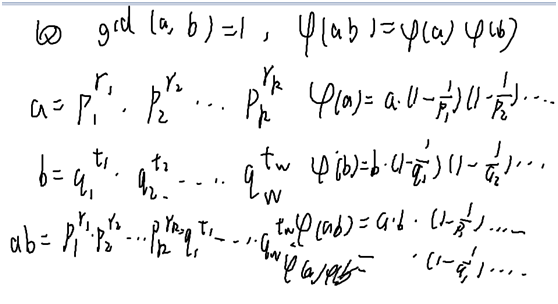
因子数τ=(r1+1)*(r2+1)*........*(r...+1)
莫比乌斯函数μ


其实就是
枚举n所有的因子的莫比乌斯函数的值的和
代码实现方面,利用埃氏筛或者线性筛来提高速度
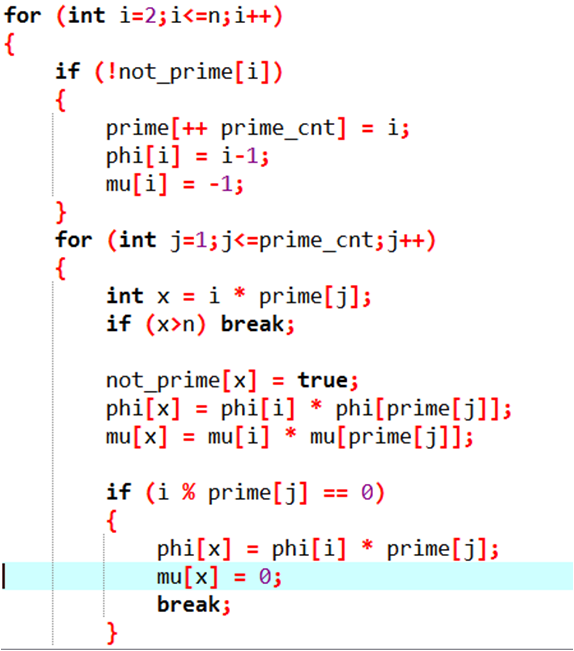
该死的莫比乌斯反演
