神经网络的基础原理

链接:

https://adventuresinmachinelearning.com/neural-networks-tutorial/

 不翻译了, 简单记录一下几个关键词和基本的原理

1.梯度下降 (gradient descendent)

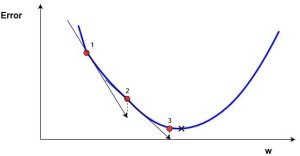
这里的梯度等价于坡度 (斜率), 就是根据导数的大小(斜率)和方向, 来逼近奇点. 比如: 导数>0, (连续区域内可导), 那么代价函数(误差函数)单调递增, 所以向左逼近极值. 反之向右.

w_new=w_old–α∗∇_error

Here ${\mathrm{wnew denotes\; the\; new w position, wold denotes\; the\; current\; or\; old w position, \nabla error is\; the\; gradient\; of\; the\; error\; at wold and \alpha is\; the\; step\; size.}}^{}$

从上可以看出, 斜率越大, 收敛速度越快. 

2.反向传播(back propagation)

输出层的偏导数是可以根据结果确定的. 之前的隐藏层, 因为第n-1层的输出为第n层的输入, 所以是嵌套函数. 假设第n-1层函数为y=f(x), 第n层函数为z=g(y), 只不过实际上g()函数和f()函数相同, 只用不同的标记便于区分.

那么根据链式法则(chain rule),  dz/dx = (dz/dy) * (dy/dx) = g'(y) * f'(x),  可以看到, 嵌套函数的导数(偏导数), 实际上是两个函数的导数(偏导数)展开相乘.

又由于最后一层(输出层)的(偏)导数可以根据结果直接推出, 对上面例子来说就是外层函数的导数 g'(y) 可以直接推出, 而f(x)是选择的固定函数, 所以f'(x)也确定. 那么倒数第二层(隐藏层中的最后一层) 的导数就是h' = g'(y) * f'(x), 同理, 倒数第三层就是h' * f'(x)

可以发现每一层的(偏)导数, 都依赖它后面一层的(偏)导数作为因子. 只有按从后向前的层序, 才能计算出结果, 这个过程叫反向传播.

3.雅可比矩阵J

由偏导数组成的矩阵, 这个矩阵并不陌生, 在IK的paper里面也用了雅可比转置法, 来迭代逼近IK结果 (https://www.cnblogs.com/crazii/p/4662199.html) , 不过那个部分我没仔细去看.

总结:

为每个节点选择固定函数f(wx+b), 并用一组值(向量x)代入便可以得到结果(向量y).

训练的过程: 已知输入x和参考输出y, 将输入带入网络, 得出的结果y0和参考结果y对比得到一个代价函数h (可以理解为误差函数或者差距函数, 比如, 具有最小值的(y-y0)²的二次曲线), 通过梯度下降, 不断迭代, 每次迭代调整w和b, 最终 使得h达到奇点(最小值), 也就是输出最接近参考值.

总结2: 感觉自己还没入门, 继续积累吧.