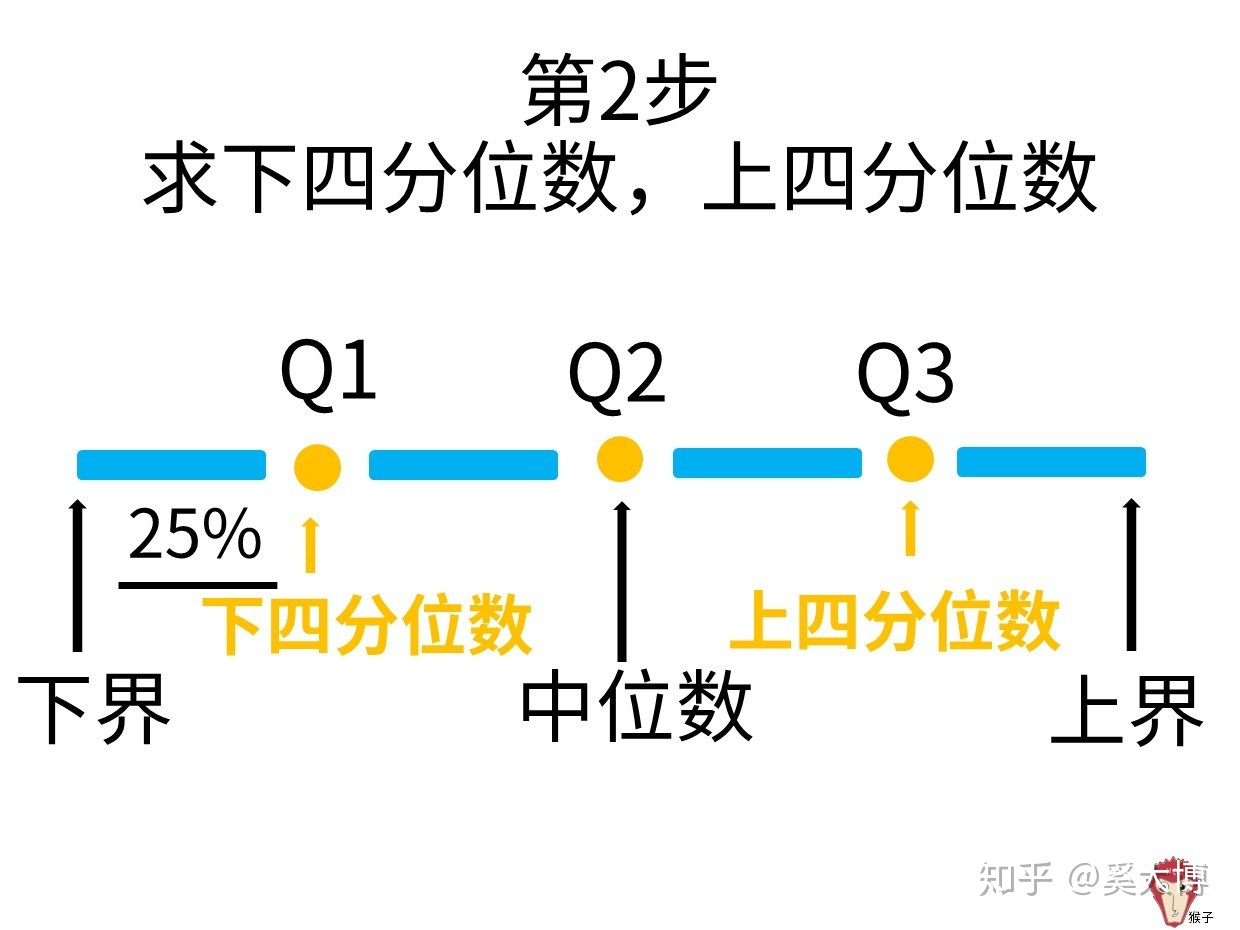
四分位数(Quartile)应用于统计学中的箱线图绘制,是统计学中分位数的一种,即把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。如下图
其中四分位数的位置算法:
- Q1的位置 = (n+1) × 0.25
- Q2的位置 = (n+1) × 0.5
- Q3的位置 = (n+1) × 0.75
注意: 当 (n+1)/ 4 不能整除时算法参考:
箱型图
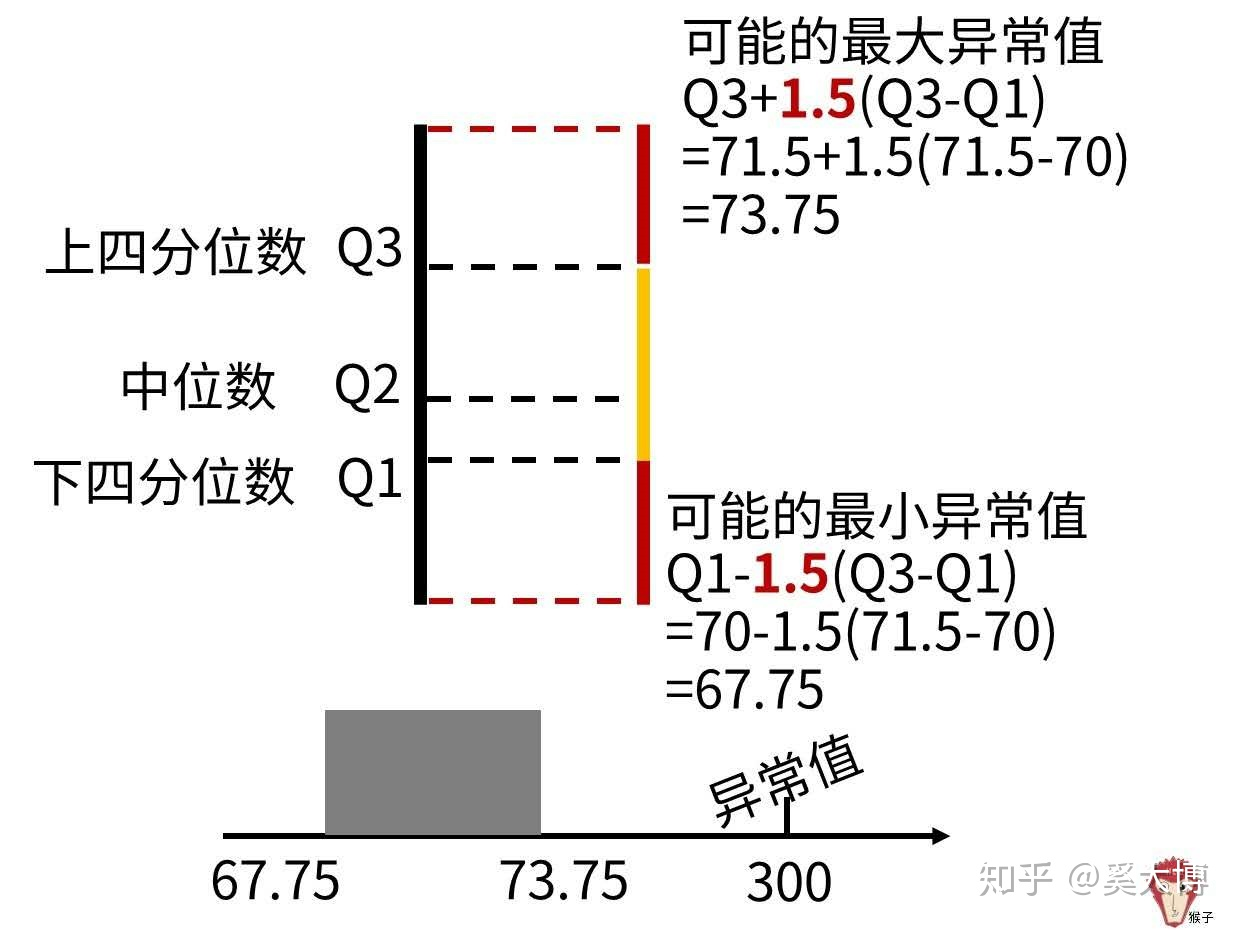
利用箱型图的四分位距(IQR)对异常值进行检测, 提供了识别异常值的一个标准:异常值通常被定义为 小于 QL-1.5IQR 或 大于 QU+1.5IQR 的值。
- QL: 称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;
- QU: 称为上四分位数,表示全部观察值中有四分之一的数据取值比它大;
- IQR:称为四分位数间距,是上四分位数QU与下四分位数QL之差,其间包含了全部观察值的一半

异常值
公式:
- 最小估计值:Q1 - k(Q3-Q1)
- 最大估计值: Q3 + k(Q3-Q1)
其中:
- K=1.5(中度异常)
- K=3 (极度异常)
当数值大于 > 最大估计值 或 数值小于 < 最小估计值,都记为异常,如下图:
说明:图中 小于67.75,大于73.75 的数值都记为异常值
总结:箱型图依据实际数据绘制,没有对数据作任何限制性要求(如服从某种特定的分布形式),它只是真实直观地表现数据分布的本来面貌;另一方面,箱型图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的鲁棒性:多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响。由此可见,箱型图识别异常值的结果比较客观,在识别异常值方面有一定的优越性
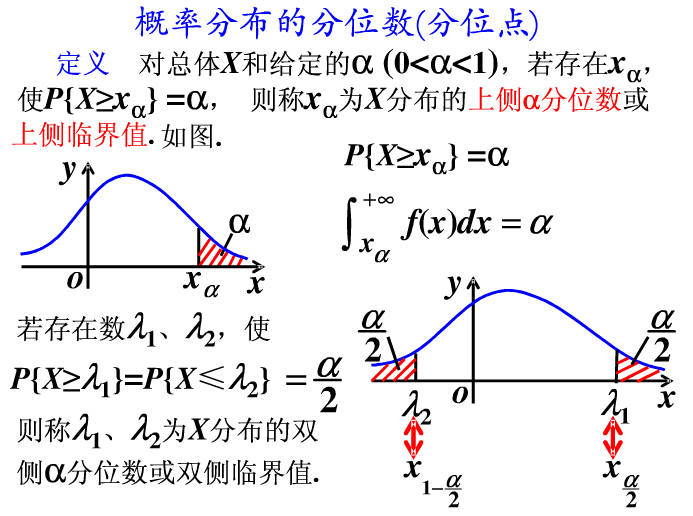
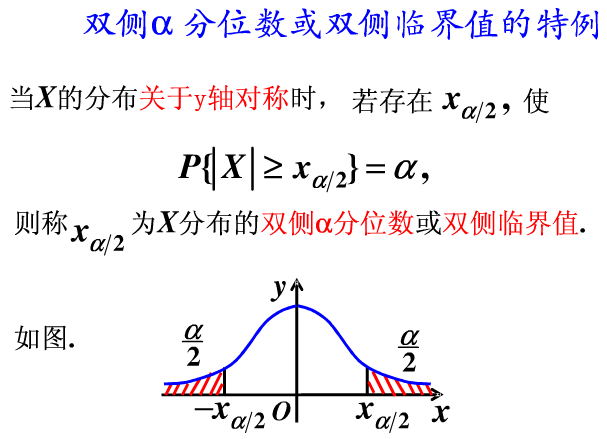
分位数
参考资料: