视频地址
Inertialization: High-Performance Animation Transitions in Gears of War
https://www.youtube.com/watch?v=BYyv4KTegJI&list=PL2e4mYbwSTbbHAJT7OdK5mv-idhlLOTl0&index=10
0x0 惯性插值和线性插值
该技术称为inertialization,微软为这个技术自己发明的新词汇,这里翻译成惯性插值。本质是多项式曲线插值。我们常用的线性插值是关于t的一次函数,而inertialization是5次。回顾一下线性插值,起始值x0和目标值x1,xt关于t的表达式为xt=(1-t)x0+tx1。当t=0时,xt=x0,当t=1时,xt=x1。惯性插值这项技术将速度和加速度,加速度的变化率(jerk)也纳入插值的考量中,维持起始值x0的速度v0和加速度a0不变,当t趋向1时,v0和a0趋向于0。因此惯性插值特别适合用在从运动到静止动画的插值。视频中举了2给例子,一个是持握武器更换方向到idle的过渡,另一个是挥手到idle的过渡。
0x0 优点
1.性能开销恒定。对比blend,blend开销随着动画数量增长而增长
2.不需要因过渡的需要而记录额外变量
3.动作过渡更自然,比如挥手到idle。但不适用于所有情况,比如反过来恐怕就不那么自然了
0x1 核心算法
只考虑1维的情况下,视频的这张图包含了全部算法。

惯性插值需要5个参数
curentValue 当前值
prevValue 当前值的上一个值
targetValue 目标值
t1 当前值和上一个值之间的时间间隔
初始速度v0和初始加速度a0可以通过公式带入得到,其中v0<0,a0>0
下面把公式转换成代码
public class InertializationMath
{
/// <summary>
/// 惯性插值
/// </summary>
/// <param name="curentValue">当前值</param>
/// <param name="prevValue">上一个值</param>
/// <param name="targetValue">目标值</param>
/// <param name="t1">当前值和上一个值的时间间隔</param>
/// <param name="t"></param>
/// <returns></returns>
public static float Lerp(float curentValue,float prevValue,float targetValue, float t1, float t)
{
float x0 = curentValue - targetValue;
float v0 = (curentValue - prevValue)/t1;
return Lerp(x0, v0, t1, t);
}
public static float Lerp(float x0, float v0, float t1, float t)
{
float tf2 = t1 * t1;
float tf3 = tf2 * t1;
float tf4 = tf3 * t1;
float tf5 = tf4 * t1;
float a0 = (-8 * v0 * t1 - 20 * x0) / (t1 * t1);
a0 = Mathf.Max(0, a0);
float A = -(a0 * tf2 + 6 * v0 * t1 + 12 * x0) / (2 * tf5);
float B = (3 * a0 * tf2 + 16 * v0 * t1 + 30 * x0) / (2 * tf4);
float C = -(3 * a0 * tf2 + 12 * v0 * t1 + 20 * x0) / (2 * tf3);
float t2 = t * t;
float t3 = t2 * t;
float t4 = t3 * t;
float t5 = t4 * t;
float xt = A * t5 + B * t4 + C * t3 + (a0 / 2) * t2 + v0 * t + x0;
return xt;
}
}
建立一个demo场景,填入你想要的参数,然后对t进行采样,使用linerenderer画下曲线,效果如下
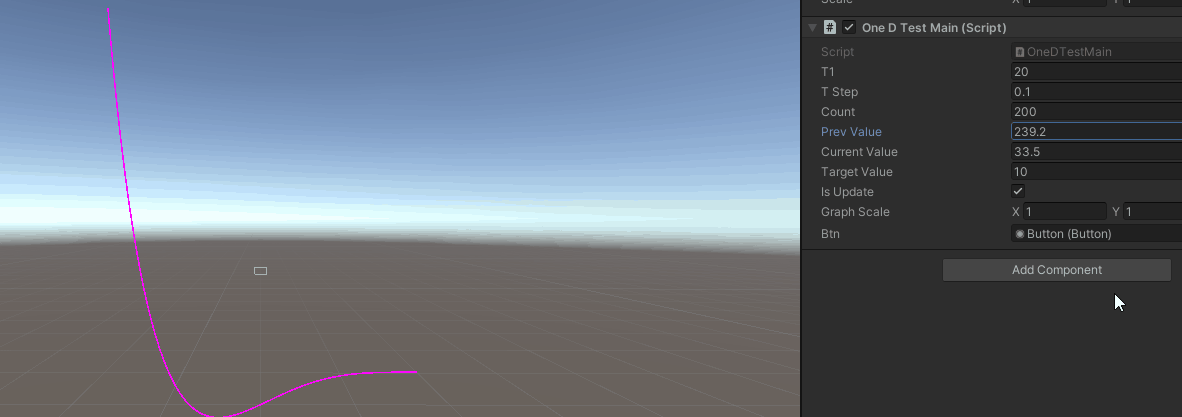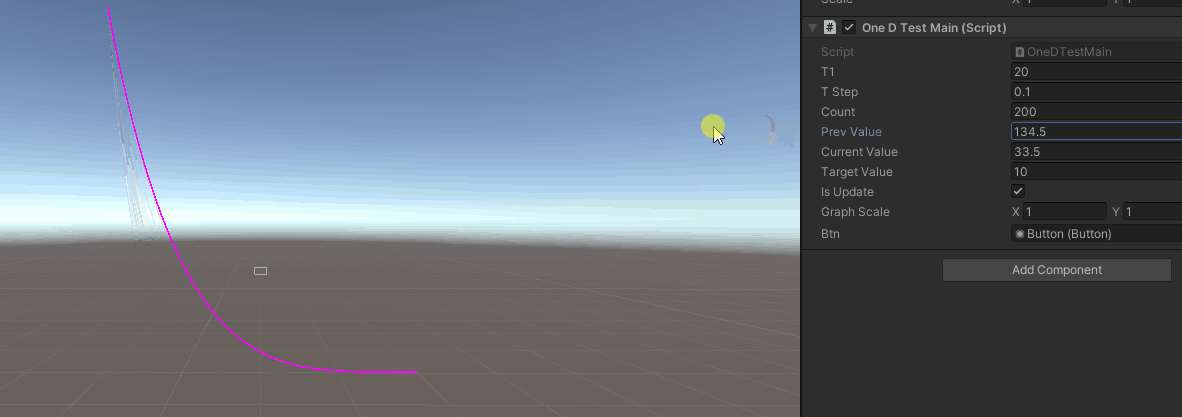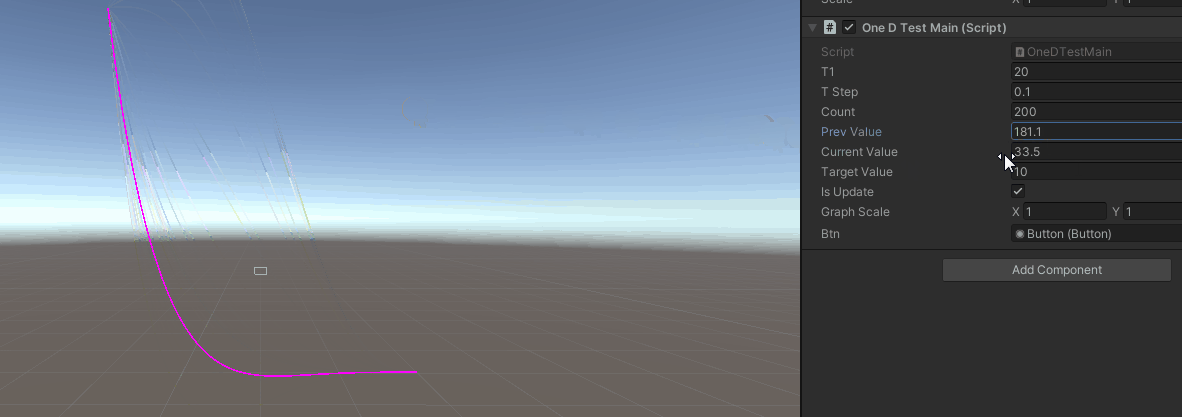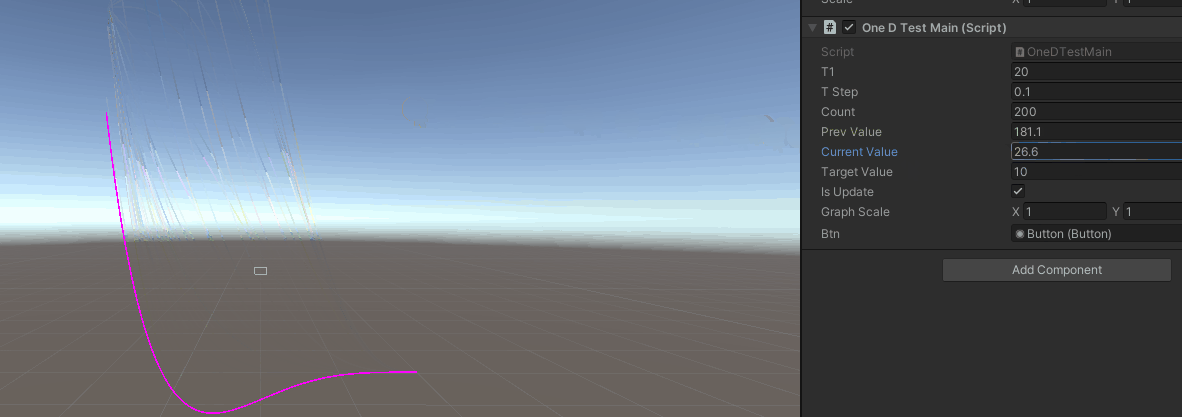
我们成功描画出了1维惯性缓动曲线。下一篇将缓动应用到3d的位移和旋转中,敬请期待。