【同余】
1、整数a,b对模m同余的充分与必要条件是m|(a-b),即a=b+mt,t是整数。
2、性质丁。若a1=b1(mod m),a2=b2(mod m),则(a1+a2)=(b1+b2)(mod m)。
推论,a+b=c(mod m),-b=-b(mod m),则a=c-b(mod m)。
3、性质戊。若a1=b1(mod m),a2=b2(mod m),则a1a2=b1b2(mod m)。
推论,ak=bk(mod m)。特别地当k=d时,a/d=b/d(mod m)。
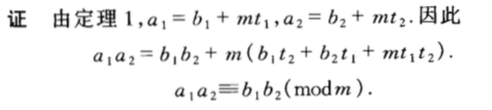
2)和 3)可得一个推论,若a=b(mod m),对任意意常量k1,k2,ak1+k2=bk1+k2(mod m)。
4、性质己。若a1d=b1d(mod m),且(d,m)=1,则a1=b1。
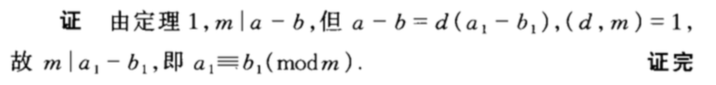
利用了定理:"12、若(a,c)=1,c|ab,则c|b。"
5、性质壬。若a=b(mod m),d|m,d>0,则 a=b(mod d)。
6、若a,b mod m同余,则(a,m)=(b,m),因为a=b+mt,即a、b,b、m的因数相同。
7、m是一个正整数,则全部整数可分成m个集合,记作K0,K1,...Km-1。其中Kr是由一切形如qm+r的整数。K0,K1,...Km-1叫做m的剩余类,若a1...am个数均在不同的剩余类,则a1...am叫做m的一个完全剩余系。
8、m个数组成完全剩余系的充要条件是两两对m不同余。
9、欧拉函数:o(a)表示 0~(a-1)中与a互质的数的个数。
10、与M素质的剩余类中各取一数,组成的集合叫简化剩余系。简化剩余系成员的个数就是欧拉函数。
11、若(a,m)=1,x通过m的简化剩余系,则ax通过m的简化剩余系。

12、若m1,m2互质,则o(m1m2)=o(m1)o(m2),o()表示欧拉函数。
13、若p是质数,则o(p^a)=p^a-p^(a-1)。
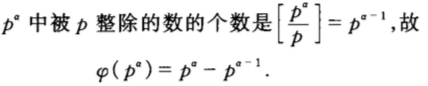
14、若 a = p^a1*p^a2*.. *pk^ak。是o(a) = a(1-1/p1)(1-1/p2).. (1- 1/pk)。

15、m1、m2是互质的两个正整数,x1、x2分别通过模m1、m2的完全剩余系,则m2x1+m1x2通过模m1m2的完全剩余系。
用反证法可轻易证明。

【不定方程】
1、二元一次不定方程:ax+by=c,若其中一解为(x0,y0),设(a,b)=d,a=a1*d,b=b1*d。则二元一次不定方程的一切解可以表示为:
x=x0-b1t,y=y0+a1t。t=0,+/-1,+/-2...
2、二元一次不定方程:ax+by=c,有解的充要条件是(a,b)|c。
3、根据定理a[(-1)^)(n-1)Qn]+b[(-1)n*Pn]=1,可以得出二元一次不定方程的其中一组解x=(-1)^(n-1)Qn,y=(-1)^n*Pn。
4、不定方程:x^2+y^2=z^2 的一切正整数解中以用下列以式表出来:
x=2ab,y=a^2-b^2, z=a^2+b^2。
【关键定理】
1、a = bq +c,则(a,b)= (b,c)。此为欧几里德法。
2、若c|ab,且(a,c)=1,则c|b。
3、a,b是任意两个不全为零的数,则存在两个数s,t,使得:as+bt=(a,b)
4、整数a,b对模m同余的充分与必要条件是m|(a-b),即a=b+mt,t是整数。
5、性质丁。若a1=b1(mod m),a2=b2(mod m),则(a1+a2)=(b1+b2)(mod m)。
6、性质戊。若a1=b1(mod m),a2=b2(mod m),则a1a2=b1b2(mod m)。
7、性质己。若a1d=b1d(mod m),且(d,m)=1,则a1=b1。
8、若(a,m)=1,x通过m的简化剩余系,则ax通过m的简化剩余系。通过反证法很容易证明。