【矩阵】
对于矩阵M=[a11,a12,a13,b11,b12,b13,c11,c12,c13],如果用P代表(a11,a12,a13), Q代表(b11,b12,b13),R代表(c11,c12,c13),并P,Q,R线性无关,则M的行可以被解释为基向量。
意即,对于向量[x,y,z],使用矩阵M的变幻相当于在以M为坐标系下的来解释x,y,z。即(xP,yQ,zR)
通常有人会认为矩阵缩放就是对角线上乘以常数k,如下:
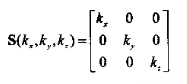
在行向量均为1,0, 0的情况下是对的。更严格的说法是,矩阵缩放是行向量乘以某个缩放常数。
【正交矩阵】
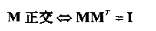
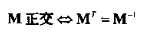
M^T=M^-1,可推出正交矩阵所有的行必须为单位向量,并且所有行互相垂直。

