实现一个简单的二叉树容器，并且实现中序、先序、后续遍历

二叉树定义：
是一种树形结构，他的特点是每个结点最多只有两颗子树（即二叉树中不存在度大于2的结点），并且二叉树的子树有左右之分，其次序不能任意颠倒。

二叉树的性质：

• 二叉树的第i层上最多有 2^(i-1) 个结点，（i>=1）；
• 深度为k的二叉树最多有 2^k - 1 个结点，（k >=1）；
• 对任何一颗二叉树，如果其终端结点数为N0，度为2的节点数为N2，那有N0 = N2 + 1;

介绍下满二叉树和完全二叉树：
满二叉树：深度为k且有2^k -1个结点的二叉树成为满二叉树。每一层上的结点的度都是2。
完全二叉树：深度为k的，有n个结点的二叉树，每一个结点都和深度为k的满二叉树中编号从1~n的结点一一对应，这样的二叉树称为完全二叉树。
如下图是满二叉树：

下面是完全二叉树，而上面的满二叉树结点序号一致：

上面介绍了些概念的东西，都是在大学的时候学习的，只可惜啊没认真学过，感觉浪费了大好青春。

在用代码实现二叉树时，我想可不可以封装成像List或者Map这类容器呢？所以在实现时我定义了内部类Node，用于表示每个结点，Node中分别定义了leftNode、rightNode表示结点的左右结点，还有个int类型的value，表示结点存储的内容。

定义的二叉树容器类中，还定义了add(int[] array)，用于将数组int[]转化成二叉树，使用Node firstNode记录二叉树的根节点。

在对二叉树进行中、先、后序的遍历。

代码如下：

package binarytree;

public class BinTree {

    // 定义一个内部类，实现节点。
    class Node{
        private Node leftNode;
        private Node rightNode;
        private int value;

        public Node(){}
        public Node(int value){
            this.value = value;
        }
        public Node getLeftNode() {
            return leftNode;
        }

        public void setLeftNode(Node leftNode) {
            this.leftNode = leftNode;
        }

        public Node getRightNode() {
            return rightNode;
        }

        public void setRightNode(Node rightNode) {
            this.rightNode = rightNode;
        }

        public int getValue() {
            return value;
        }

        public void setValue(int value) {
            this.value = value;
        }
    }

    // 记录二叉树的根结点
    private Node firstNode;

    // 返回二叉树根结点
    public Node getFirstNode() {
        return firstNode;
    }

    // 根据int数组创建二叉树，构造函数
    public BinTree(int[] values){
        Node node = null;
        for (int i = 0; i < values.length; i++){
            if (i == 0){
                node = new Node(values[i]);
            }else{
                add(node, values[i]);
            }
        }
        firstNode = node;
    }

    // 向二叉树中添加元素
    public void add(Node node, int value){
        if(node == null){
            return;
        }
        // 小于第一个节点的值，放入左边
        if(value <= node.getValue()){
            if(node.getLeftNode() == null){
                Node tempNode = new Node(value);
                node.setLeftNode(tempNode);
            }else{
                node = node.getLeftNode();
                add(node, value);
            }
        }
        // 值大于当前结点的值，放在右子树
        if (value > node.getValue()){
            if(node.getRightNode() == null){
                Node tempNode = new Node(value);
                node.setRightNode(tempNode);
            }else{
                node = node.getRightNode();
                add(node, value);
            }
        }
    }
    // 中序遍历
    public void zhongXu(Node node){
        if (node == null){
            return;
        }
        zhongXu(node.getLeftNode());
        System.out.print(node.getValue() + " ");
        zhongXu(node.getRightNode());
    }
    // 先序遍历
    public void xianXu(Node node){
        if(node == null){
            return;
        }
        System.out.print(node.getValue() + " ");
        xianXu(node.getLeftNode());
        xianXu(node.getRightNode());
    }

    // 后序遍历
    public void houXu(Node node){
        if (node == null){
            return;
        }
        houXu(node.getLeftNode());
        houXu(node.getRightNode());
        System.out.print(node.getValue() + " ");
    }
}

下面进行测试，测试代码如下：

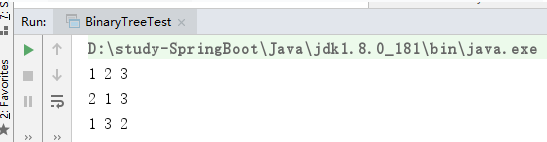
package binarytree;

public class BinaryTreeTest {

    public static void main(String[] args){
        int[] values = new int[]{2, 1, 3};//中序：123 先序：213 后序：132
        BinTree binTree = new BinTree(values);
        binTree.zhongXu(binTree.getFirstNode());
        binTree.xianXu(binTree.getFirstNode());
        binTree.houXu(binTree.getFirstNode());

    }
}

运行结果：

总结：
二叉树的3中遍历方式，主要是针对根结点（或者说是父结点）来说，然后左边始终先于右边。
中序遍历即将根结点放在中间遍历：左结点 -> 根结点 -> 右结点
先序遍历即将根结点放在最先遍历：根结点 -> 左结点 -> 右结点
后序遍历即将根结点放在最后遍历：左结点 -> 右结点 -> 根结点
遍历代码，需要注意递归的停止条件是：if(node == null);