全文链接:http://tecdat.cn/?p=3232
原文出处:拓端数据部落公众号
检测异常值的4种方法和R语言时间序列分解异常检测
什么是异常值?
异常值是与其他观测值有显著差异的数据点。异常值会显著扭曲特征分布和ML工作,因此我们需要观察并形成处理它们的策略。
异常值是如何出现的?
这种观察的出现可能是由以下原因引起的:
- 测量方法的差异,例如,传感器的灵敏度发生了变化;
- 实验误差,其中异常值可能是数据收集过程中错误的结果;
- 引入新方法;
- 数据收集阶段或数据处理过程中的错误;
- 或观测值中方差的指示符。
根据异常值的性质,您可以保留它们或排除它们,例如,在实验错误的情况下,您希望删除它们。
异常值的类型有哪些?
有 3 种类型的异常值:
- 全局:也称为点异常值。这一观察结果远远超出了整个数据集的范围。例如:在一个班级中,所有学生的年龄都是相同的,但有一个关于500岁学生的记录。

2. 条件:根据上下文,观察样本被认为是异常的。例如,由于全球经济危机,一个国家的经济表现急剧下降,一段时间内较低的利率成为常态。
3. 集合:一组彼此接近且具有接近异常值的观测值。如果点的子集作为聚合值与整个数据集显著偏离,但单个数据点的值本身在上下文或全局意义上都不是异常的:

为什么识别异常值很重要?
机器学习算法对值的范围和分布很敏感。异常值可能会误导 ML 模型,导致训练时间延长、准确性降低,最终导致结果更差。但是,并非所有ML工作都受到异常值的影响,对于某些算法,您可以安全地忽略它们。
- 异常值敏感算法:线性回归、逻辑回归、支持向量机
- 异常免疫算法:所有基于树或复杂的算法
在业务方面,您应该了解为什么存在异常值,并且您可以将其删除。例如,如果您有一个表示人身高的要素,并且其中一个观测值包含一个字符串,而不是一个字符串,其奇怪值如 = “abc cm”,并且由于高度不能包含此类值,因此可以安全地将其删除。
如何检测异常值?
您可以通过使用不同类型的视觉效果轻松发现异常值:

以下是箱线图显示的内容:
- 中位数是位于排名序列中心的元素的值。请注意,中位数受异常值的影响较小,因此在中心显示的是中位数,而不是算术平均值。
- 前四分位数(Q3 或 75%)是分数,只有 25% 的值高于该分数。下四分位数(Q1 或 25%)是低于该值的值,只有 25% 的值。
- 四分位间距 (IQR) 是 75% 和 25% 四分位数之间的差值。在此范围内有 50% 的值。例如,如果范围很窄,则子组的成员在评估中是一致的。如果它是宽泛的,那么就没有同质的意见。
基于上述情况,您通常可以检测到高于“25% 百分位减去 1.5 x IQR”或低于“75% 百分位加 1.5 x IQR”的异常值,如上图所示。

直方图将数值数据聚合到称为条柱的均匀间隔组中,并显示每个条柱中值出现的频率。条形图是使用数字字段或百分比/比率字段创建的。直方图有助于回答以下问题:值的分布是什么,它们在数据集中出现的频率如何?
通过增加和减少条柱的数量,您可以影响数据分析的方式。虽然数据本身不会更改,但其外观可能会更改。选择正确数量的条柱对于正确解释数据中的模式非常重要。太少的条柱可以隐藏一些模式,太多的条柱会夸大小的、可接受的数据更改的价值。正确的条柱数量将揭示在使用箱线图时不可见的模式。
3. 散点图

散点图显示两个变量之间集合元素的分布。一个独立参数的值沿 X 轴绘制,第二个从属参数的值沿 Y 轴绘制。
散点图上显示的模式可用于查看不同类型的相关性。从点的一般聚类/相关线中显著移除的点称为异常值。
4. Z 得分
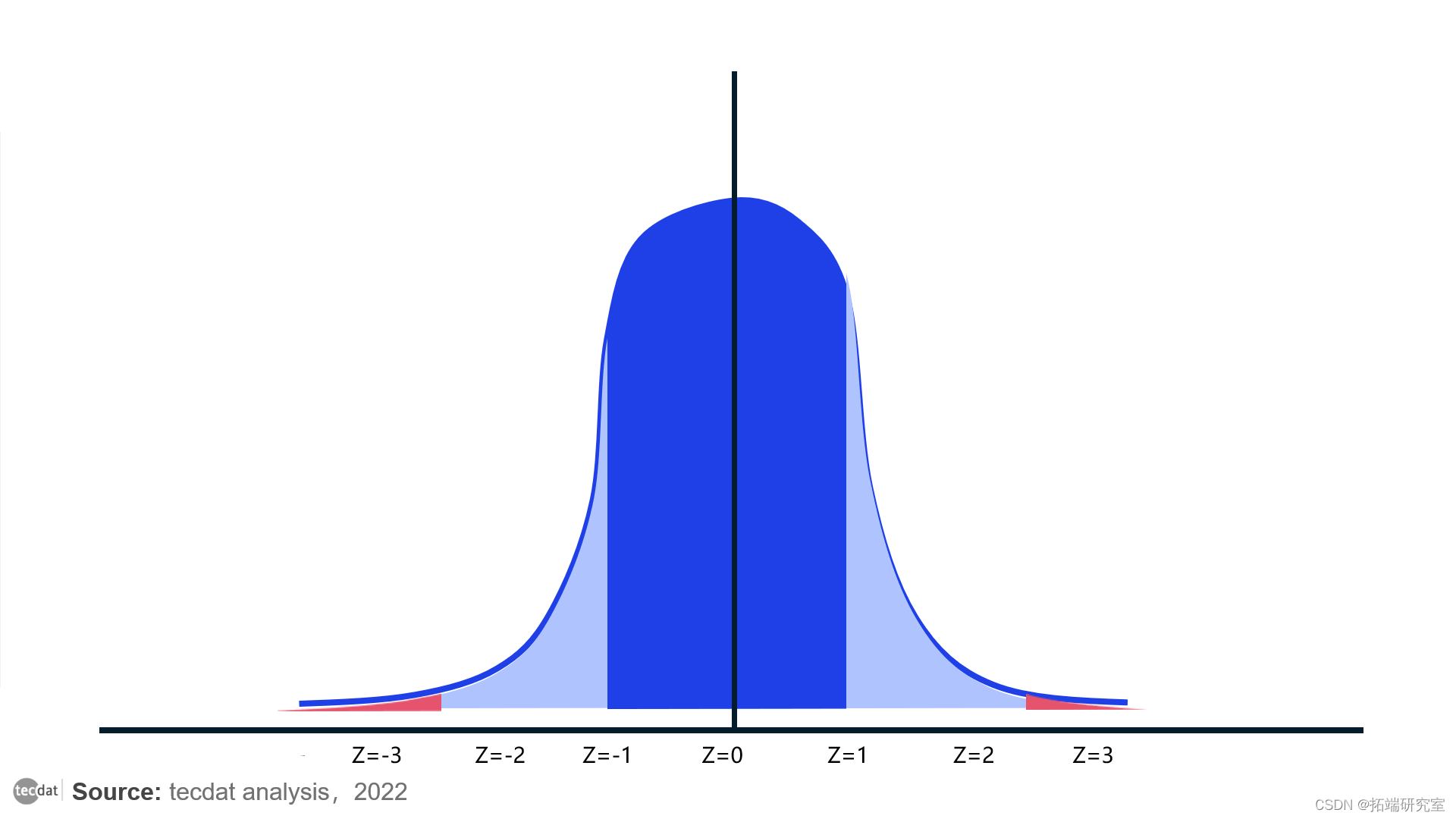
z 得分也可以称为标准分数,用于表示数据相对于均值的分布。此分数表示低于或高于给定总体的标准差数。
z 的值可以在钟形曲线上看到。其中 Z 得分的范围从 -3 个标准差(正态分布曲线的最左边角)到 +3 个标准差(正态分布曲线的最右边角)。在大多数情况下,大于或小于 -+3 的值被标识为异常值。
如何处理异常值?
在数据集中检测到异常值后,您需要执行以下 3 类操作:
- 删除异常值。通常,如果您对数据应该落在哪个范围内有很好的了解,例如人们的年龄,则可以删除异常值,您可以安全地删除超出该范围的值。
- 更改异常值的值(例如,将值替换为平均值或最大值,例如90%百分位)
- 保留它。例如,如果 20%-40% 的数据是异常值,则不应将其视为异常值,而应进一步研究它。
案例研究
我们最近有一个很棒的机会与一位客户合作,要求构建一个适合他们需求的异常检测算法。业务目标是准确地检测各种营销数据的异常情况,这些数据包括跨多个客户和Web源数千个时间序列的网站操作和营销反馈。异常检测算法,该算法基于时间并可从一个到多个时间序列进行扩展。
我们与许多教授数据科学的客户合作,并利用我们的专业知识加速业务发展。
我们的客户遇到了一个具有挑战性的问题:按时间顺序检测每日或每周数据的时间序列异常。异常表示异常事件,可能是营销域中的Web流量增加或IT域中的故障服务器。无论如何,标记这些不寻常的事件确保业务顺利运行非常重要。其中一个挑战是客户处理的不是一个时间序列,而是需要针对这些极端事件进行分析。
anomalize
这里有四个简单步骤的工作要点。
-
第1步:安装
-
-
install.packages("tidyverse")
-
-
第2步:加载
-
-
library(tidyverse)
-
-
-
第3步:收集时间序列数据
-
-
-
tidyverse\_cran\_downloads
-
-
## # A tibble: 6,375 x 3
-
-
## # Groups: package \[15\]
-
-
## date count package
-
-
##
-
-
## 1 2017-01-01 873. tidyr
-
-
## 2 2017-01-02 1840. tidyr
-
-
## 3 2017-01-03 2495. tidyr
-
-
## 4 2017-01-04 2906. tidyr
-
-
## 5 2017-01-05 2847. tidyr
-
-
## 6 2017-01-06 2756. tidyr
-
-
## 7 2017-01-07 1439. tidyr
-
-
## 8 2017-01-08 1556. tidyr
-
-
## 9 2017-01-09 3678. tidyr
-
-
## 10 2017-01-10 7086. tidyr
-
-
## # ... with 6,365 more rows
-
-
第4步:异常化
-
-
使用功能及时发现异常情况。


异常检测工作流程
其中包括:
-
用时间序列分解
-
用检测异常
-
异常下限和上限转换
点击标题查阅往期内容
PYTHON中用PROPHET模型对天气时间序列进行预测与异常检测
左右滑动查看更多
01

02
03
04

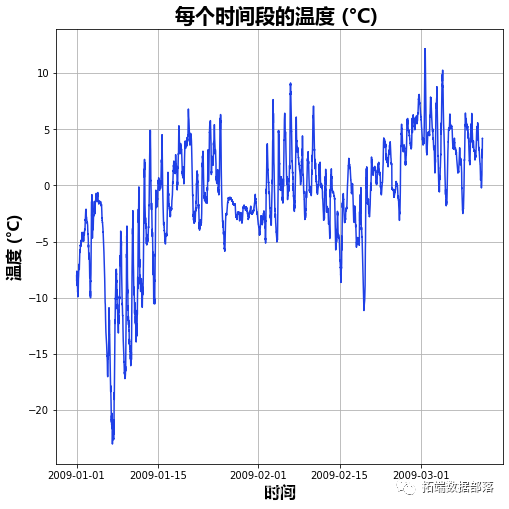
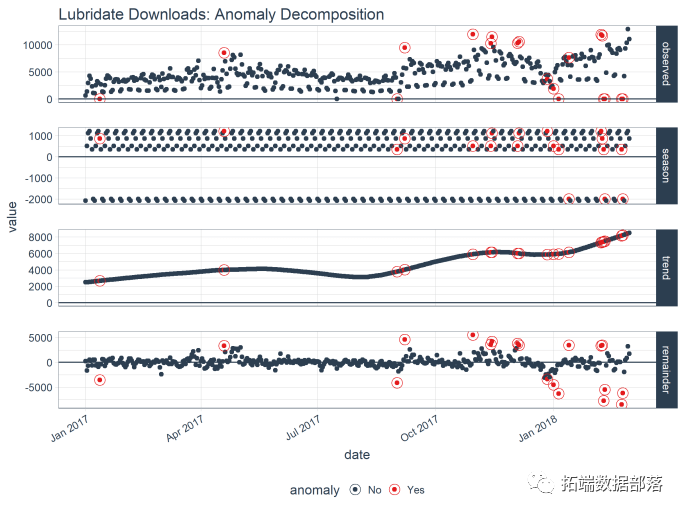
时间序列分解
第一步是使用时间序列分解。“计数”列被分解为“观察”,“季节”,“趋势”和“剩余”列。时间序列分解的默认值是method = "stl",使用平滑器进行季节性分解。
-
## # A time tibble: 6,375 x 6
-
-
## # Index: date
-
-
## # Groups: package \[15\]
-
-
## package date observed season trend remainder
-
-
##
-
-
## 1 tidyr 2017-01-01 873. -2761. 5053. -1418.
-
-
## 2 tidyr 2017-01-02 1840. 901. 5047. -4108.
-
-
## 3 tidyr 2017-01-03 2495. 1460. 5041. -4006.
-
-
## 4 tidyr 2017-01-04 2906. 1430. 5035. -3559.
-
-
## 5 tidyr 2017-01-05 2847. 1239. 5029. -3421.
-
-
## 6 tidyr 2017-01-06 2756. 367. 5024. -2635.
-
-
## 7 tidyr 2017-01-07 1439. -2635. 5018. -944.
-
-
## 8 tidyr 2017-01-08 1556. -2761. 5012. -695.
-
-
## 9 tidyr 2017-01-09 3678. 901. 5006. -2229.
-
-
## 10 tidyr 2017-01-10 7086. 1460. 5000. 626.
-
-
## # ... with 6,365 more rows

frequency并trend自动为您选择。此外,可以通过输入基于时间的周期(例如“1周”或“2个季度”)来更改选择,可以确定有多少观察属于时间跨度。
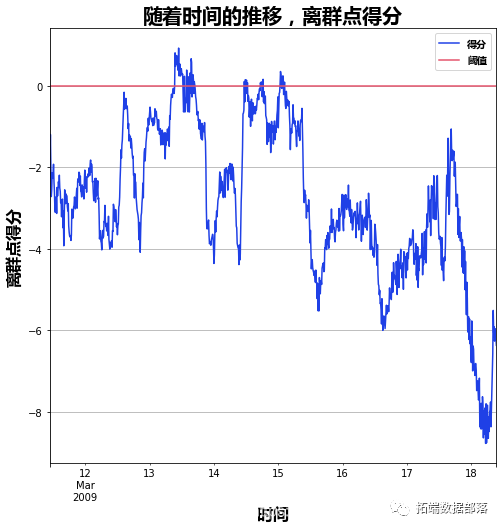
异常检测
下一步是对分解的数据执行异常检测。产生了三个新列:“remainder\_l1”(下限),“remainder\_l2”(上限)和“异常”(是/否标志)。默认方法是method = "iqr",在检测异常时快速且相对准确。
-
## # Groups: package \[15\]
-
-
## package date observed season trend remainder remainder_l1
-
-
##
-
-
## 1 tidyr 2017-01-01 873. -2761. 5053. -1418. -3748.
-
-
## 2 tidyr 2017-01-02 1840. 901. 5047. -4108. -3748.
-
-
## 3 tidyr 2017-01-03 2495. 1460. 5041. -4006. -3748.
-
-
## 4 tidyr 2017-01-04 2906. 1430. 5035. -3559. -3748.
-
-
## 5 tidyr 2017-01-05 2847. 1239. 5029. -3421. -3748.
-
-
## 6 tidyr 2017-01-06 2756. 367. 5024. -2635. -3748.
-
-
## 7 tidyr 2017-01-07 1439. -2635. 5018. -944. -3748.
-
-
## 8 tidyr 2017-01-08 1556. -2761. 5012. -695. -3748.
-
-
## 9 tidyr 2017-01-09 3678. 901. 5006. -2229. -3748.
-
-
## 10 tidyr 2017-01-10 7086. 1460. 5000. 626. -3748.
-
-
## # ... with 6,365 more rows, and 2 more variables: remainder_l2 ,
-
-
## # anomaly

现在尝试另一个绘图功能。它只适用于单个时间序列。“季节”消除每周的季节性。趋势是平滑的。最后,检测最重要的异常值。
-
tidyverse\_cran\_downloads %>%
-
-
-
time_decompose(count, method = "stl", frequency = "auto", trend = "auto") %>%
-
-
anomalize(remainder, method = "iqr", alpha = 0.05, max_anoms = 0.2) %>%
-
-
-
plot\_anomaly\_decomposition() +
异常下限和上限
最后一步是围绕“观察”值创建下限和上限。创建了两个新列:“recomposed\_l1”(下限)和“recomposed\_l2”(上限)。
-
## # A time tibble: 6,375 x 11
-
-
## # Index: date
-
-
## # Groups: package \[15\]
-
-
## package date observed season trend remainder remainder_l1
-
-
##
-
-
## 1 tidyr 2017-01-01 873. -2761. 5053. -1418. -3748.
-
-
## 2 tidyr 2017-01-02 1840. 901. 5047. -4108. -3748.
-
-
## 3 tidyr 2017-01-03 2495. 1460. 5041. -4006. -3748.
-
-
## 4 tidyr 2017-01-04 2906. 1430. 5035. -3559. -3748.
-
-
## 5 tidyr 2017-01-05 2847. 1239. 5029. -3421. -3748.
-
-
## 6 tidyr 2017-01-06 2756. 367. 5024. -2635. -3748.
-
-
## 7 tidyr 2017-01-07 1439. -2635. 5018. -944. -3748.
-
-
## 8 tidyr 2017-01-08 1556. -2761. 5012. -695. -3748.
-
-
## 9 tidyr 2017-01-09 3678. 901. 5006. -2229. -3748.
-
-
## 10 tidyr 2017-01-10 7086. 1460. 5000. 626. -3748.
-
-
## # ... with 6,365 more rows, and 4 more variables: remainder_l2 ,
-
-
## # anomaly , recomposed\_l1 , recomposed\_l2

让我们看一下“lubridate”数据。我们可以plot\_anomalies()和设置time\_recomposed = TRUE。此功能适用于单个和分组数据。
-
time_decompose(count, method = "stl", frequency = "auto", trend = "auto") %>%
-
-
anomalize(remainder, method = "iqr", alpha = 0.05, max_anoms = 0.2) %>%
-
-
time_recompose() %>%
-
-
# 绘制异常分解
-
-
plot\_anomalies(time\_recomposed = TRUE) +
-
-
ggtitle("Lubridate Downloads: Anomalies Detected")
预测
forecast是在执行预测之前有效收集异常值的好方法。它使用基于STL的离群值检测方法。它非常快,因为最多有两次迭代来确定异常值带。
结论
R软件非常有效地用于检测异常的许多传统预测时间序列。但是,速度是一个问题,特别是在尝试扩展到多个时间序列时。
我们从中了解到所有软件包的最佳组合:
-
分解方法:我们包括两个时间序列分解方法:( "stl"使用Loess的传统季节分解)和"twitter"(使用中间跨度的季节分解)。
-
异常检测方法:我们包括两种异常检测方法:( "iqr"使用类似于3X IQR的方法forecast::tsoutliers())和"gesd"(使用Twitter使用的GESD方法AnomalyDetection)。
有问题欢迎下方留言!

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言时间序列分解和异常检测方法应用案例》。
点击标题查阅往期内容
R语言指数平滑法holt-winters分析谷歌Google Analytics博客用户访问时间序列数据
PYTHON中用PROPHET模型对天气时间序列进行预测与异常检测
R语言用LOESS(局部加权回归)季节趋势分解(STL)进行时间序列异常检测
Matlab中的偏最小二乘法(PLS)回归模型,离群点检测和变量选择
R语言分布滞后线性和非线性模型(DLNM)分析空气污染(臭氧)、温度对死亡率时间序列数据的影响
Python面板时间序列数据预测:格兰杰因果关系检验Granger causality test药品销售实例与可视化
R语言从经济时间序列中用HP滤波器,小波滤波和经验模态分解等提取周期性成分分析
R语言计量经济学:工具变量法(两阶段最小二乘法2SLS)线性模型分析人均食品消费时间序列数据和回归诊断
R语言用标准最小二乘OLS,广义相加模型GAM ,样条函数进行逻辑回归LOGISTIC分类
R语言用线性模型进行预测:加权泊松回归,普通最小二乘,加权负二项式模型,多重插补缺失值
PYTHON用时变马尔可夫区制转换(MRS)自回归模型分析经济时间序列
R语言经济学:动态模型平均(DMA)、动态模型选择(DMS)预测原油时间序列价格
R语言从经济时间序列中用HP滤波器,小波滤波和经验模态分解等提取周期性成分分析
R语言使用灰色关联分析(Grey Relation Analysis,GRA)中国经济社会发展指标
R语言从经济时间序列中用小波滤波和经验模式分解等提取周期性成分分析
R语言实现偏最小二乘回归法 partial least squares (PLS)回归
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归