原文链接:http://tecdat.cn/?p=23305
原文出处:拓端数据部落公众号
什么是支持向量机 (SVM)?
我们将从简单的理解 SVM 开始。
【视频】支持向量机SVM、支持向量回归SVR和R语言网格搜索超参数优化实例
支持向量机SVM、支持向量回归SVR和R语言网格搜索超参数优化实例
,时长07:24
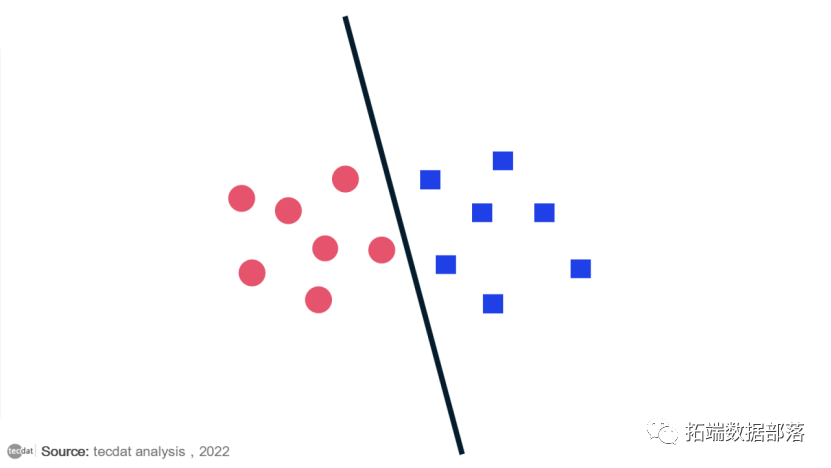
假设我们有两个标签类的图,如下图所示:
你能决定分隔线是什么吗?你可能想出了这个:
这条线将类完全分开。这就是 SVM 本质上所做的——简单的类分离。
现在,数据是这样的:

在这里,我们没有一条简单的线来分隔这两个类。所以我们将扩展我们的维度并沿 z 轴引入一个新维度。

我们现在可以将这两个类分开:

这正是 SVM 所做的!它试图找到分隔这两个类的线/超平面(在多维空间中)。然后根据要预测的类别,根据它是位于超平面的正面还是负面,对新点进行分类。
支持向量机 (SVM) 算法的超参数
在继续之前,您应该了解 SVM 的一些重要参数:
-
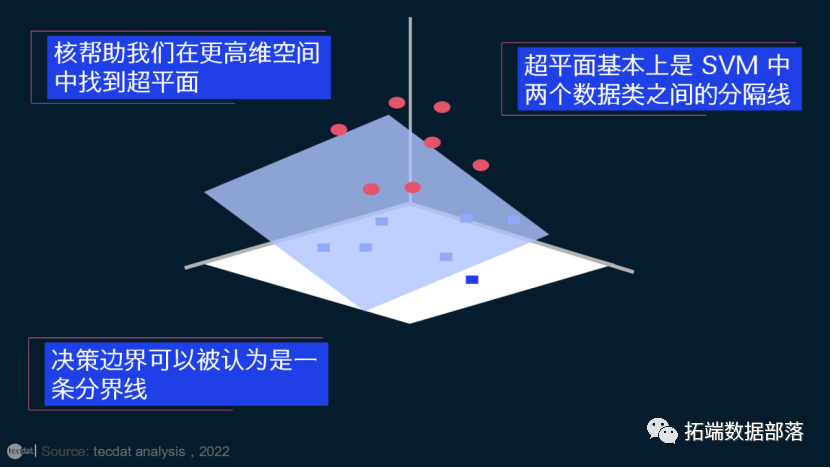
核:核帮助我们在更高维空间中找到超平面,而不会增加计算成本。通常,如果数据的维度增加,计算成本会增加。当我们无法在给定维度中找到分离超平面并且需要在更高维度中移动时,需要增加维度:
-
超平面:这基本上是 SVM 中两个数据类之间的分隔线。但在支持向量回归中,这条线将用于预测连续输出
-
决策边界:决策边界可以被认为是一条分界线(为简化起见),其一侧是正例,另一侧是负例。在这条线上,这些例子可以分为正面或负面。SVM 的相同概念也将应用于支持向量回归
支持向量回归 (SVR) 简介
支持向量回归 (SVR) 使用与 SVM 相同的原理,但用于回归问题。让我们花几分钟时间了解 SVR 背后的想法。
支持向量回归背后的想法
回归的问题是在训练样本的基础上找到一个近似映射从输入域到实数的函数。因此,现在让我们深入了解 SVR 的实际工作原理。
将这两条绿线视为决策边界,将蓝线视为超平面。当我们继续使用 SVR 时,我们的目标是基本上考虑决策边界线内的点。我们的最佳拟合线是具有最大点数的超平面。

我们首先要了解的是什么是决策边界。将这些线视为距超平面的任何距离,例如“a”。因此,这些是我们在距超平面“+a”和“-a”距离处绘制的线。文中的这个'a'基本上被称为epsilon。
假设超平面的方程如下:
Y = wx+b(超平面方程)
则决策边界方程变为:
wx+b=+a
wx+b= -a
因此,任何满足我们的 SVR 的超平面都应该满足:
-a < Y- wx+b < +a
我们的主要目标是在距原始超平面“a”距离处确定决策边界,以便最接近超平面的数据点或支持向量位于该边界线内。
因此,我们将只选取那些在决策边界内且错误率最低的点,或者在公差范围内的点。这给了我们一个更好的拟合模型。
接下来,我们将展示如何使用R语言来进行支持向量回归SVR。
R语言进行支持向量机回归SVR和网格搜索超参数优化
我们将首先做一个简单的线性回归,然后转向支持向量回归,这样你就可以看到两者在相同数据下的表现。
一个简单的数据集
首先,我们将使用这个简单的数据集。
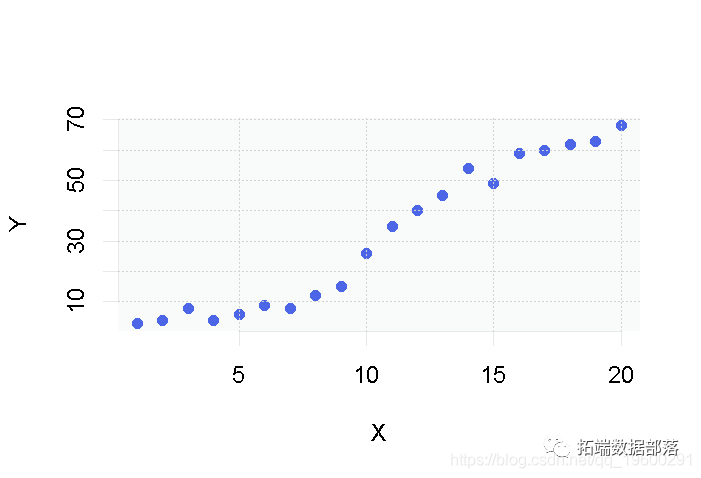
正如你所看到的,在我们的两个变量X和Y之间似乎存在某种关系,看起来我们可以拟合出一条在每个点附近通过的直线。
我们用R语言来做吧!
第1步:在R中进行简单的线性回归
下面是CSV格式的相同数据,我把它保存在regression.csv文件中。

我们现在可以用R来显示数据并拟合直线。
# 从csv文件中加载数据 dataDirectory <- "D:/" #把你自己的文件夹放在这里 data <- read.csv(paste(dataDirectory, 'data.csv', sep=""), header = TRUE) # 绘制数据 plot(data, pch=16) # 创建一个线性回归模型 model <- lm(Y ~ X, data) # 添加拟合线 abline(model)
上面的代码显示以下图表:

第2步:我们的回归效果怎么样?
为了能够比较线性回归和支持向量回归,我们首先需要一种方法来衡量它的效果。
为了做到这一点,我们改变一下代码,使模型做出每一个预测可视化
# 对每个X做一个预测 pred <- predict(model, data) # 显示预测结果 points(X, pred)
产生了以下图表。

对于每个数据点Xi,模型都会做出预测Y^i,在图上显示为一个红色的十字。与之前的图表唯一不同的是,这些点没有相互连接。
为了衡量我们的模型效果,我们计算它的误差有多大。
我们可以将每个Yi值与相关的预测值Y^i进行比较,看看它们之间有多大的差异。
请注意,表达式Y^i-Yi是误差,如果我们做出一个完美的预测,Y^i将等于Yi,误差为零。
如果我们对每个数据点都这样做,并将误差相加,我们将得到误差之和,如果我们取平均值,我们将得到平均平方误差(MSE)。

在机器学习中,衡量误差的一个常见方法是使用均方根误差(RMSE),所以我们将使用它来代替。
为了计算RMSE,我们取其平方根,我们得到RMSE

使用R,我们可以得到以下代码来计算RMSE
rmse <- function(error)
{
sqrt(mean(error^2))
}

我们现在知道,我们的线性回归模型的RMSE是5.70。让我们尝试用SVR来改善它吧!
第3步:支持向量回归
用R创建一个SVR模型。
下面是用支持向量回归进行预测的代码。
model <- svm(Y ~ X , data)
如你所见,它看起来很像线性回归的代码。请注意,我们调用了svm函数(而不是svr!),这是因为这个函数也可以用来用支持向量机进行分类。如果该函数检测到数据是分类的(如果变量是R中的一个因子),它将自动选择SVM。
代码画出了下面的图。

这一次的预测结果更接近于真实的数值 ! 让我们计算一下支持向量回归模型的RMSE。
# 这次svrModel$residuals与data$Y - predictedY不一样。 #所以我们这样计算误差 svrPredictionRMSE

正如预期的那样,RMSE更好了,现在是3.15,而之前是5.70。
但我们能做得更好吗?
第四步:调整你的支持向量回归模型
为了提高支持向量回归的性能,我们将需要为模型选择最佳参数。
在我们之前的例子中,我们进行了ε-回归,我们没有为ε(ϵ)设置任何值,但它的默认值是0.1。 还有一个成本参数,我们可以改变它以避免过度拟合。
选择这些参数的过程被称为超参数优化,或模型选择。
标准的方法是进行网格搜索。这意味着我们将为ϵ和成本的不同组合训练大量的模型,并选择最好的一个。
# 进行网格搜索 tuneResultranges = list(epsilon = seq(0,1,0.1), cost = 2^(2:9)) # 绘制调参图 plot(Result)
在上面的代码中有两个重要的点。
-
我们使用tune方法训练模型,ϵ=0,0.1,0.2,...,1和cost=22,23,24,...,29这意味着它将训练88个模型(这可能需要很长一段时间
-
tuneResult返回MSE,别忘了在与我们之前的模型进行比较之前将其转换为RMSE。
最后一行绘制了网格搜索的结果。
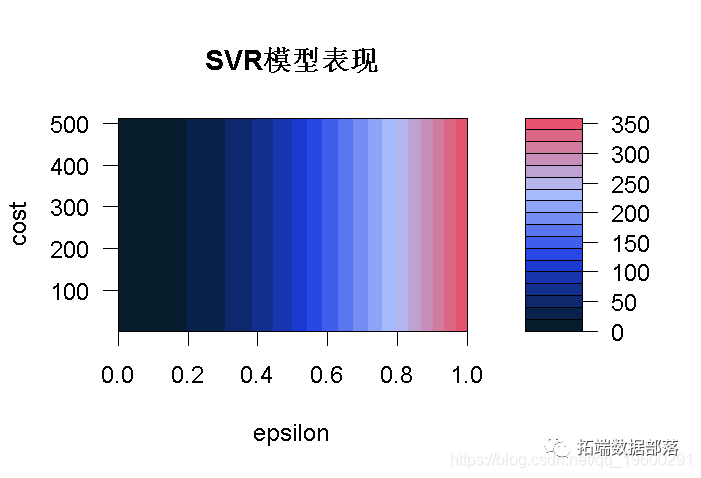
在这张图上,我们可以看到,区域颜色越深,我们的模型就越好(因为RMSE在深色区域更接近于零)。
这意味着我们可以在更窄的范围内尝试另一个网格搜索,我们将尝试在0和0.2之间的ϵ值。目前看来,成本值并没有产生影响,所以我们将保持原样,看看是否有变化。
rangelist(epsilo = seq(0,0.2,0.01), cost = 2^(2:9))
我们用这一小段代码训练了不同的168模型。
当我们放大暗区域时,我们可以看到有几个较暗的斑块。
从图中可以看出,C在200到300之间,ϵ在0.08到0.09之间的模型误差较小。

希望对我们来说,我们不必用眼睛去选择最好的模型,R让我们非常容易地得到它,并用来进行预测。
# 这个值在你的电脑上可能是不同的 # 因为调参方法会随机调整数据 tunedModelRMSE <- rmse(error)

我们再次提高了支持向量回归模型的RMSE !
我们可以把我们的两个模型都可视化。在下图中,第一个SVR模型是红色的,而调整后的SVR模型是蓝色的。
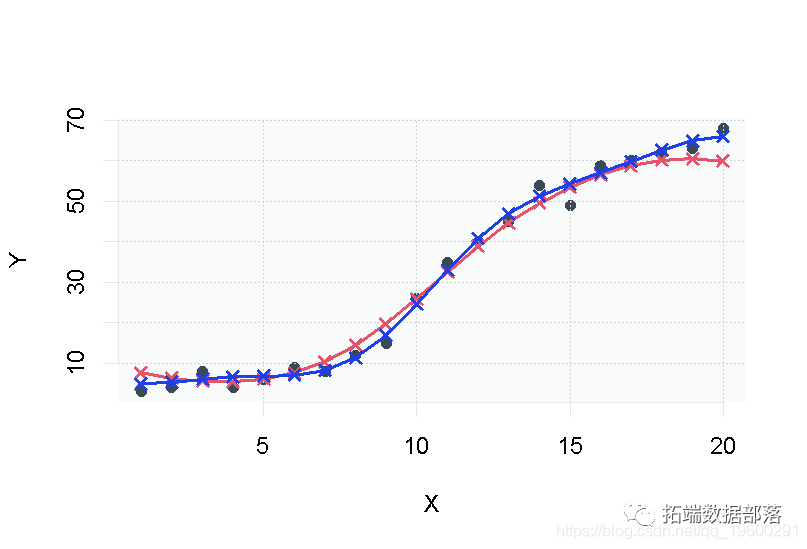
我希望你喜欢这个关于用R支持向量回归的介绍。你可以查看原文得到本教程的源代码。

本文摘选《R语言进行支持向量机回归SVR和网格搜索超参数优化》,点击“阅读原文”获取全文完整资料。
点击标题查阅往期内容
逻辑回归、随机森林、SVM支持向量机预测心脏病风险数据和模型诊断可视化
R语言梯度提升机 GBM、支持向量机SVM、正则判别分析RDA模型训练、参数调优化和性能比较可视化分析声纳数据
Matlab建立SVM,KNN和朴素贝叶斯模型分类绘制ROC曲线
基于数据挖掘SVM模型的pre-incident事故预防预测
Python中基于网格搜索算法优化的深度学习模型分析糖尿病数据
R语言深度学习:用keras神经网络回归模型预测时间序列数据
Matlab用深度学习长短期记忆(LSTM)神经网络对文本数据进行分类
R语言KERAS深度学习CNN卷积神经网络分类识别手写数字图像数据(MNIST)
Python中用PyTorch机器学习神经网络分类预测银行客户流失模型
SAS使用鸢尾花(iris)数据集训练人工神经网络(ANN)模型
【视频】R语言实现CNN(卷积神经网络)模型进行回归数据分析
R语言用神经网络改进Nelson-Siegel模型拟合收益率曲线分析
matlab使用长短期记忆(LSTM)神经网络对序列数据进行分类
使用PYTHON中KERAS的LSTM递归神经网络进行时间序列预测