吴恩达机器学习笔记整理——单变量线性回归

通过模型分析,拟合什么类型的曲线。
一、基本概念
1.训练集
由训练样例(training example)组成的集合就是训练集(training set), 如下图所示,其中(x,y)是一个训练样本,训练集中每一行表示一个训练样本;(x^i,y^i)表示第i个训练样本。

2.假设函数h
使用某种学习算法对训练集的数据进行训练, 我们可以得到假设函数(Hypothesis Function), 如下图所示. 在房价的例子中,假设函数就是一个房价关于房子面积的函数。有了这个假设函数之后, 给定一个房子的面积我们就可以预测它的价格了.
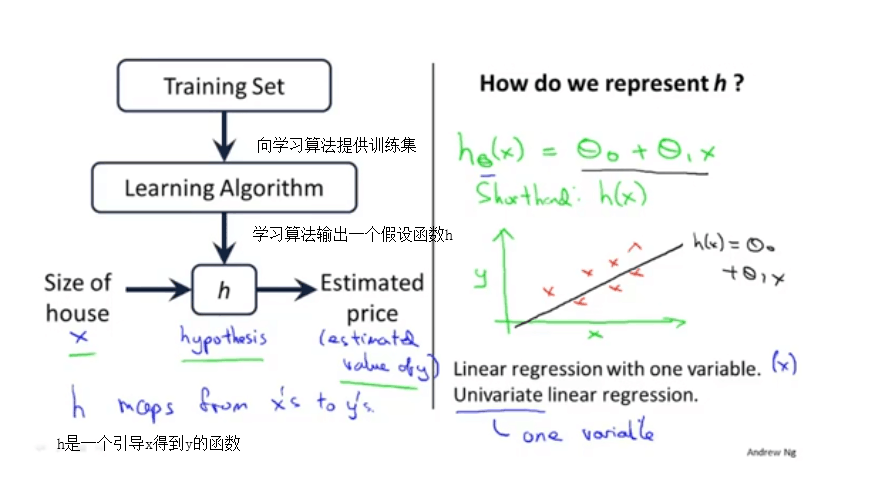
这个模型就叫做单变量的线性回归(Linear Regression with One Variable).
二、代价函数
1.概念
对于不同的假设函数, 假设函数中有两个未知的量当选择不同的,所得到的模型的效果肯定是不一样的. 如下图所示, 列举了三种不同的下的假设函数

代价函数,是使所得直线与数据最大程度拟合,使h(x)在输入x后所得的y值,最接近样本对应的y值,此时的参数θ1和θ0即所求。
越是接近, 代表这个假设函数越是准确, 这里我们选择均方误差来作为衡量标准, 即我们想要每个样例的估计值与真实值之间差的平方的均值最小。用公式表达为:

(1/2是为了便于后续计算)记:

这样就得到了我们的代价函数(cost function), 也就是我们的优化目标, 我们想要代价函数最小:
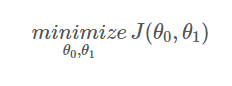

2.代价函数与假设函数
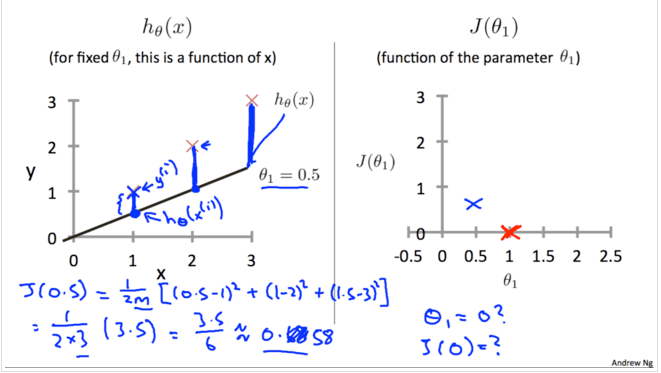
现在为了更方便地探究hθ(x)与J(θ0,θ1)的关系, 先令θ0等于0, 得到了简化后的假设函数,有假设函数的定义可知此时的假设函数是经过原点的直线. 相应地也也得到简化的代价函数。如图所示:

简化之后,我们令θ1等于1, 就得到hθ(x)=x如下图左所示。图中三个红叉表示训练样例,通过代价函数的定义我们计算得出J(1)=0,对应下图右中的(1,0)坐标。

重复上面的步骤,再令θ1=0.5,得到hθ(x)如下图左所示。通过计算得出J(0.5)=0.58,对应下图右中的(0.5,0.58)坐标。
对于不同的θ1,对应着不同的假设函数hθ(x),于是就有了不同的J(θ1)的值。将这些点连接起来就可以得到J(θ1)关于θ1的函数图像,如下图所示:
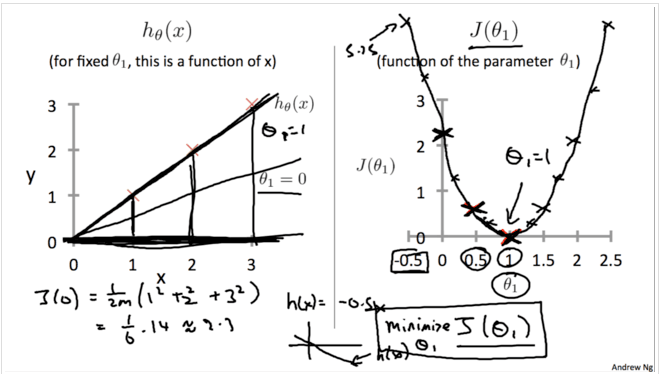
我们的目标就是找到一个θ使得J(θ)最小, 通过上面的描点作图的方式, 我们可以从图中看出, 当θ1=1的时候, J(θ)取得最小值.
我们令θ0等于0, 并且通过设置不同的θ1来描点作图得到J(θ1)的曲线。这一节我们不再令θ0=0, 而是同时设置θ0和θ1的值, 然后再绘出J(θ0,θ1)的图形. 因为此时有两个变量,很容易想到J(θ1)应该是一个曲面, 如下图所示:
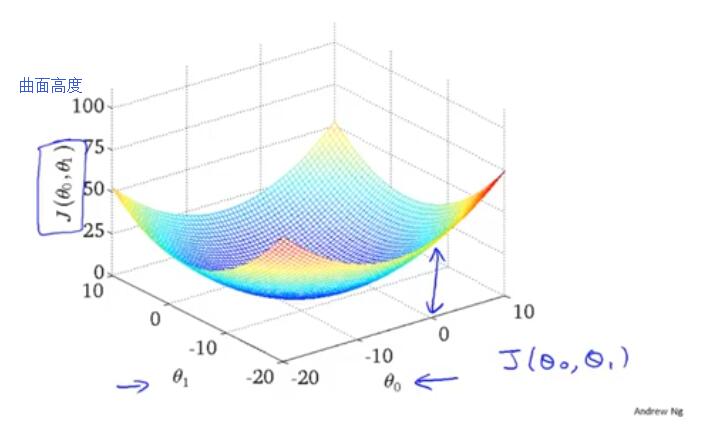
为了便于研究,我们采用等高线图来研究3D模型,在地理中常用等高线用来描述地形
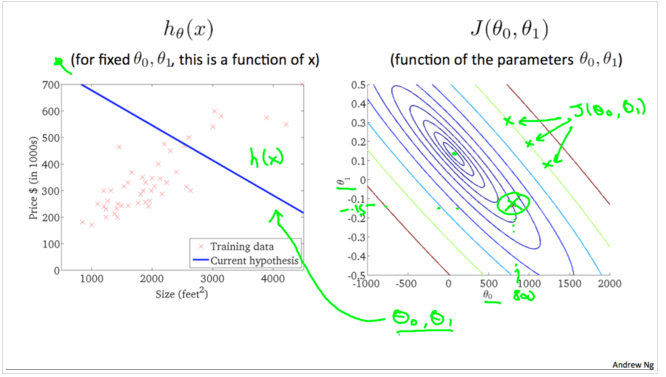
下图右,越靠近中心表示J(θ0,θ1)的值越小(对应3D图中越靠近最低点的位置)。下图左表示当=800, θ1=0.15的时候对应的hθ(x),通过θ0, θ1的值可以找到下图右中Jθ0,θ1)的值。对于不同的拟合直线,对应不同的J(θ0,θ1)
对于斜率为负的情形:
当斜率为0,情形如下:

最优拟合情形:
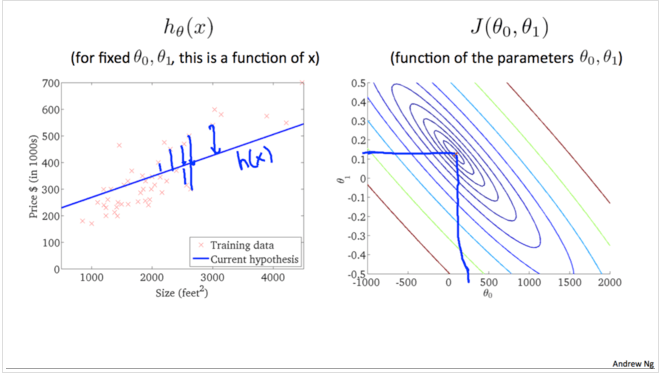
我们在这个过程中不断由外向内趋近,直至找到一个最接近最佳hθ(x),这个过程就是梯度下降的过程。
三、梯度下降算法
1.梯度下降
梯度下降算法是一种优化算法, 它可以帮助我们找到一个函数的局部极小值点. 它不仅仅可以用在线性回归模型中, 在机器学习许多其他的模型中也可以使用它. 对于我们现在研究的单变量线性回归来说, 我们想要使用梯度下降来找到最优的θ0,θ1.它的思想是, 首先随机选择两个θ0,θ1(例如, θ0=0,θ1=0), 不断地改变它们的值使得J(θ)变小, 最终找到J(θ)的最小值点.

可以把梯度下降的过程想象成下山坡, 如果想要尽可能快的下坡, 应该每次都往坡度最大的方向下山.

梯度下降算法得到的结果会受到初始状态的影响, 即当从不同的点开始时, 可能到达不同的局部极小值, 如下图:

下面具体看一下算法的过程, 如下图所示, 其中:=表示赋值,α叫做学习率用来控制下降的幅度,导数部分叫做梯度。这里一定要注意的是,算法每次是同时(simultaneously)改变θ0和θ1的值,如图下图所示。

3.梯度和学习率
我们先来看看梯度下降算法的梯度是如何帮助我们找到最优解的. 为了研究问题的方便我们还是同样地令θ0等于0,假设一开始选取的θ1在最低点的右侧,此时的梯度(斜率)是一个正数。根据上面的算法更新θ1的时候,它的值会减小, 即靠近最低点。

类似地假设一开始选取的θ1在最低点的左侧,此时的梯度是一个负数,根据上面的算法更新θ1的时候,它的值会增大,也会靠近最低点.

如果一开始选取的θ1恰好在最适位置,那么更新θ1时,它的值不会发生变化。

学习率α会影响梯度下降的幅度。如果α太小, θ的值每次会变化的很小,那么梯度下降就会非常慢;相反地,如果α过大,θ的值每次会变化会很大,有可能直接越过最低点,可能导致永远没法到达最低点。

由于随着越来越接近最低点, 相应的梯度(绝对值)也会逐渐减小,所以每次下降程度就会越来越小, 我们并不需要减小α的值来减小下降程度。

3.计算梯度
根据定义, 梯度也就是代价函数对每个θ的偏导:

我们将hθ(x(i))=θ0+θ1x(i)带入到J(θ0,θ1)中,并且分别对θ0和θ1求导得:

由此得到了完整的梯度下降算法

还记得这个图吗, 前面说了梯度下降算法得到的结果会受初始状态的影响, 即初始状态不同, 结果可能是不同的局部最低点.

事实上,用于线性回归的代价函数总是一个凸函数(Convex Function)。这样的函数没有局部最优解,只有一个全局最优解。所以我们在使用梯度下降的时候,总会得到一个全局最优解。

迭代多次后,我们得到了最优解。现在我们可以用最优解对应的假设函数来对房价进行预测了。例如一个1,250平方英尺的房子大概能卖到250k$,如下图所示:

