【视频】R语言生存分析原理与晚期肺癌患者分析案例|数据分享

原文链接：http://tecdat.cn/?p=10278

原文出处：拓端数据部落公众号

生存分析（也称为工程中的可靠性分析）的目标是在协变量和事件时间之间建立联系。生存分析的名称源于临床研究，其中预测死亡时间，即生存，通常是主要目标。

视频：R语言生存分析原理与晚期肺癌患者分析案例

R语言生存分析Survival analysis原理与晚期肺癌患者分析案例

，时长08:41

生存分析是一种回归问题（人们想要预测一个连续值），但有一个转折点。它与传统回归的不同之处在于，在生存分析中，结果变量既有一个事件，也有一个与之相关的时间值，部分训练数据只能被部分观察——它们是被删失的。本文用R语言生存分析晚期肺癌患者数据（查看文末了解数据获取方式）。

普通最小二乘回归方法不足，因为事件发生的时间通常不是正态分布的，并且模型无法处理删失，但这在生存数据中很常见。

为什么要做生存分析：右删失

在某些情况下，可能无法观察到事件时间：这通常称为 右删失。在以死亡为事件的临床试验中，当发生以下情况之一时，就会发生这种情况。1。当一定数量的参与者死亡时，研究结束。2。参与者退出研究。3。 研究达到预定的结束时间，并且一些参与者存活到结束。在每种情况下，幸存的参与者离开研究后，我们都不知道他们会发生什么。然后我们有一个问题：

当对于某些个体，我们只观察到他们的事件时间的下限时，我们如何对经验分布进行建模或进行非负回归？

上图说明了右删失。对于参与者 1，我们看到他们何时死亡。参与者 2 退出了，我们知道他们一直活到那时，但不知道后来发生了什么。对于参与者 3，我们知道他们活到了预定的研究结束，但又不知道之后发生了什么。

生存函数和风险函数

生存分析中的两个关键工具是生存函数和风险函数。

生存函数：它是一个函数，用于给出我们有兴趣知道的任何对象是否会在任何指定时间之后存活的概率。在数学上它可以由以下公式表示 

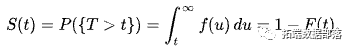
其中 S(t) 是一个生存函数，其中 T 是一个连续随机变量，是一个事件的时间。F(t) 是区间[0,∞) 上的累积分布函数。

我们也可以用风险函数来写生存函数。假设事件尚未发生 ，风险率λ(t) 是事件在时间t发生的瞬时概率的主要值。

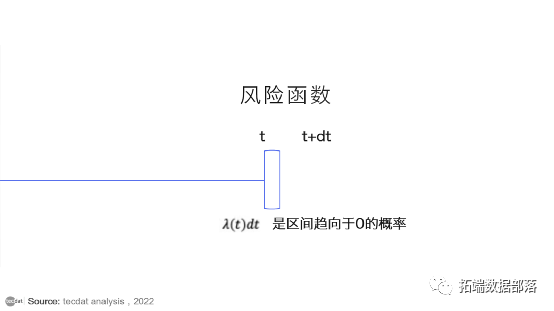
那么关键问题是如何估计风险和/或生存函数。

Kaplan Meier的非参数估计

在非参数生存分析中，我们要估计生存函数没有协变量，并且有删失。如果我们没有删失，我们可以从经验 CDF 开始. 这个等式简洁地表示：

有多少人随着时间的推移而死亡? 那么生存函数就是：还有多少人还活着？

但是，我们无法回答一些人被时间t删失时提出的这个问题.

虽然我们不一定知道有多少人在任意时间t幸存下来，我们知道研究中有多少人仍然处于风险之中。我们可以使用它来代替。将学习时间划分区间, 其中每个ti是参与者的事件时间或删失时间。假设参与者只能在观察到的事件时间失效。假设没有人在同一时间死去（没有关系），我们可以查看每次有人死去的时间。我们说在那个特定时间死亡的概率是，并说在任何其他时间死亡的概率是0.

在温和的假设下，包括参与者具有独立且相同分布的事件时间，并且删失和事件时间是独立的，这给出了一个一致的估计量。上图给出了一个简单案例的 Kaplan Meier 估计示例。

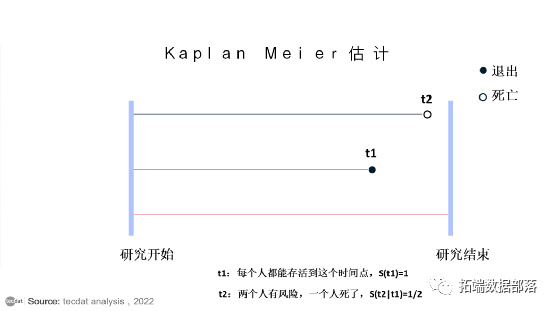
生存分析用于各种领域

例如：

• 用于患者生存时间分析的癌症研究，

• “事件历史分析”的社会学，

• 在工程中用于“故障时间分析”。

在癌症研究中，典型的研究问题如下：

• 某些临床特征对患者生存有何影响

• 一个人能活3年的概率是多少？

• 患者组之间的生存率是否存在差异？

第1部分：生存分析简介 

本演示文稿将介绍生存分析 ，参考：

Clark, T., Bradburn, M., Love, S., & Altman, D. (2003). Survival analysis part I: Basic concepts and first analyses. 232-238. ISSN 0007-0920.

我们今天将使用的一些软件包包括：

• lubridate

1.  
   library(survival)
2.  
    

什么是生存数据？

事件时间数据由不同的开始时间和结束时间组成。

癌症的例子

• 从手术到死亡的时间

• 从治疗开始到进展的时间

• 从响应到复发的时间

其他领域的例子

事件发生时间数据在许多领域都很常见，包括但不限于

• 从艾滋病毒感染到艾滋病发展的时间

• 心脏病发作的时间

• 药物滥用发生的时间

• 机器故障时间

生存分析别名

由于生存分析在许多其他领域很常见，因此也有其他名称

• 可靠性分析

• 持续时间分析

• 事件历史分析

• 事件发生时间分析

肺数据集

数据包含来自北中部癌症治疗组的晚期肺癌患者。今天我们将用来演示方法的一些变量包括

• 时间：以天为单位的生存时间

• 状态：删失状态1 =删失，2 =失效

• 性别：男= 1女= 2

删失类型

某个主题可能由于以下原因而被删失：

• 后续损失

• 退出研究

• 固定学习期结束前没有活动

具体来说，这些是删失的示例。

分配随访时间

• 受删失的主题仍会提供信息，因此必须适当地包含在分析中

• 随访时间的分布存在偏差，在接受检查的患者和有事件的患者之间可能有所不同

生存数据的组成部分

对于主题ii：

• 活动时间Ti

• 删失时间Ci

• 事件指标δi：

• 1，如果观察到的事件（即  Ti≤CiTi≤Ci）

• 如果检查，则为0（即  Ti>CiTi>Ci）

1. 观测时间Yi=min(Ti,Ci)Yi=min(Ti,Ci)

lung数据中提供了观察时间和事件指示

• 时间：以天为单位的生存时间（YiYi）

• 状态：删失状态1 =删失，2 =死亡（δiδi）

在R中处理日期

数据通常带有开始日期和结束日期，而不是预先计算的生存时间。第一步是确保将这些格式设置为R中的日期。

让我们创建一个小的示例数据集，其中sx_date包含手术日期和last_fup_date上次随访日期的变量。

1.  
   date_ex <- 
2.  
     tibble(
3.  
       sx_date = c("2007-06-22", "2004-02-13", "2010-10-27"), 
4.  
       last\_fup\_date = c("2017-04-15", "2018-07-04", "2016-10-31")
5.  
       )
6.  
    
7.  
   date_ex

1.  
   ## # A tibble: 3 x 2
2.  
   ##   sx\_date    last\_fup_date
3.  
   ##   <chr>      <chr>        
4.  
   ## 1 2007-06-22 2017-04-15   
5.  
   ## 2 2004-02-13 2018-07-04   
6.  
   ## 3 2010-10-27 2016-10-31

我们看到它们都是字符变量，通常都是这种情况，但是我们需要将它们格式化为日期。

格式化日期-基数R

1.  
   date_ex %>% 
2.  
     mutate(
3.  
       sx\_date = as.Date(sx\_date, format = "%Y-%m-%d"), 
4.  
       last\_fup\_date = as.Date(last\_fup\_date, format = "%Y-%m-%d") 
5.  
       )

1.  
   ## # A tibble: 3 x 2
2.  
   ##   sx\_date    last\_fup_date
3.  
   ##   <date>     <date>       
4.  
   ## 1 2007-06-22 2017-04-15   
5.  
   ## 2 2004-02-13 2018-07-04   
6.  
   ## 3 2010-10-27 2016-10-31

• 请注意，R格式必须包含分隔符和符号。例如，如果您的日期格式为m / d / Y，则需要format = "%m/%d/%Y"

格式化日期-lubridate程序包

我们还可以使用该lubridate包来格式化日期。在这种情况下，请使用ymd功能

1.  
   date_ex %>% 
2.  
     mutate(
3.  
       sx\_date = ymd(sx\_date), 
4.  
       last\_fup\_date = ymd(last\_fup\_date)
5.  
       )

1.  
   ## # A tibble: 3 x 2
2.  
   ##   sx\_date    last\_fup_date
3.  
   ##   <date>     <date>       
4.  
   ## 1 2007-06-22 2017-04-15   
5.  
   ## 2 2004-02-13 2018-07-04   
6.  
   ## 3 2010-10-27 2016-10-31

• 请注意，与基本R选项不同，不需要指定分隔符

计算生存时间 

现在日期已格式化，我们需要以某些单位（通常是几个月或几年）计算开始时间和结束时间之间的差。在base中R，用于difftime计算两个日期之间的天数，然后使用将其转换为数字值as.numeric。然后将除以365.25年的平均天数转换为年。

1.  
   date_ex %>% 
2.  
     mutate(
3.  
       os_yrs = 
4.  
         as.numeric(
5.  
           difftime(last\_fup\_date, 
6.  
                    sx_date, 
7.  
                    units = "days")) / 365.25
8.  
       )

1.  
   ## # A tibble: 3 x 3
2.  
   ##   sx\_date    last\_fup\_date os\_yrs
3.  
   ##   <date>     <date>         <dbl>
4.  
   ## 1 2007-06-22 2017-04-15      9.82
5.  
   ## 2 2004-02-13 2018-07-04     14.4 
6.  
   ## 3 2010-10-27 2016-10-31      6.01

计算生存时间 

操作员可以%--%指定一个时间间隔，然后使用将该时间间隔转换为经过的秒数as.duration，最后除以dyears(1)，将其转换为年数，从而得出一年中的秒数。

1.  
   ## # A tibble: 3 x 3
2.  
   ##   sx\_date    last\_fup\_date os\_yrs
3.  
   ##   <date>     <date>         <dbl>
4.  
   ## 1 2007-06-22 2017-04-15      9.82
5.  
   ## 2 2004-02-13 2018-07-04     14.4 
6.  
   ## 3 2010-10-27 2016-10-31      6.02

事件标标

对于生存数据的组成部分，我提到了事件指示器：

事件指标δiδi：

• 1，如果观察到的事件（即  Ti≤CiTi≤Ci）

• 如果检查，则为0（即  Ti>CiTi>Ci）

在lung数据中，我们有：

• 状态：删失状态1 =删失，2 =失效

生存函数

受试者可以存活超过指定时间的概率

S(t)=Pr(T>t)=1−F(t)S(t)=Pr(T>t)=1−F(t)

S(t)S(t)：生存函数F(t)=Pr(T≤t)F(t)=Pr(T≤t)：累积分布函数

理论上，生存函数是平滑的；在实践中，我们以离散的时间尺度观察事件。

生存概率

• 生存概率在某个时间，S(t)S(t)，是存活超过该时间，考虑到个体已存活刚刚在此之前，时间的条件概率。

• 可以估计为当时活着但没有损失的随访患者人数除以当时的活着患者人数

• 生存概率的Kaplan-Meier估计是这些条件概率的乘积

• 在时间0，生存概率为1，即  S(t0)=1S(t0)=1

创建生存对象

Kaplan-Meier方法是估计生存时间和概率的最常用方法。这是一种非参数方法，可产生阶跃函数，每次事件发生时，阶跃下降。

• 创建一个生存对象。对于每个主题，将有一个条目作为生存时间，+如果主题是经过删失的，则后面跟一个。让我们看一下前10个观察值：

##  \[1\]  306   455  1010+  210   883  1022+  310   361   218   166

用Kaplan-Meier方法估算生存曲线

• 该survfit函数根据公式创建生存曲线。让我们为整个同类群组生成总体生存曲线，将其分配给object f1，然后查看names该对象的：

names(f1)

1.  
   ##  \[1\] "n"          "time"       "n.risk"     "n.event"    "n.censor"  
2.  
   ##  \[6\] "surv"       "std.err"    "cumhaz"     "std.chaz"   "start.time"
3.  
   ## \[11\] "type"       "logse"      "conf.int"   "conf.type"  "lower"     
4.  
   ## \[16\] "upper"      "call"

该survfit对象将用于创建生存曲线的一些关键组件包括：

• time，其中包含每个时间间隔的起点和终点

• surv，其中包含每个对应的生存概率 time

Kaplan-Meier图 

现在， 绘制对象 获得Kaplan-Meier图。

1.  
   plot(survfit(Surv(time, status) ~ 1, data = lung), 
2.  
    

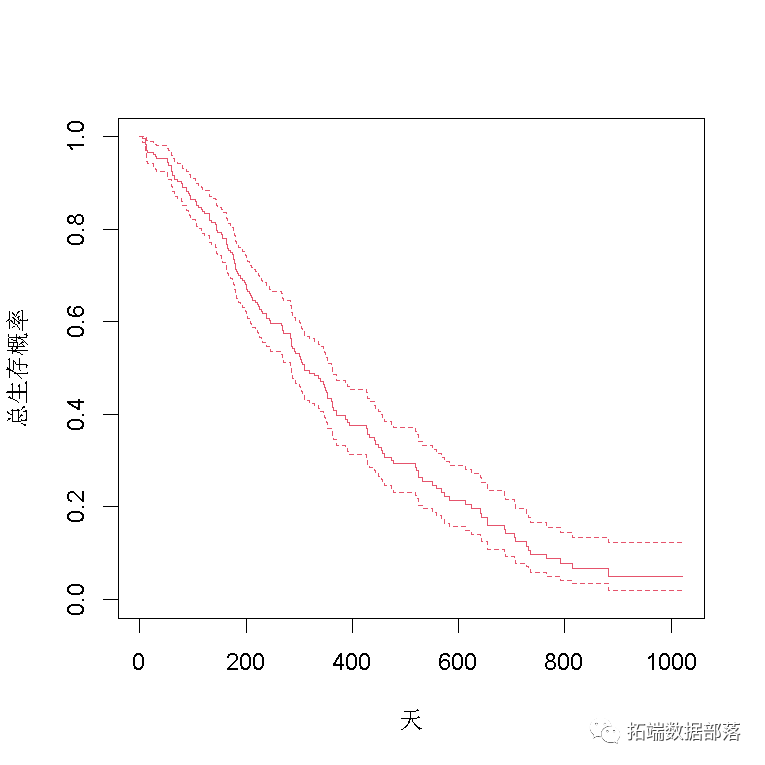
• 基数R中的默认图显示了具有相关置信区间（虚线）的阶跃函数（实线）

• 水平线代表间隔的生存时间

• 时间间隔由事件终止

• 垂直线的高度显示累积概率的变化

• 带有刻度线的经过删失的观察结果会减少间隔之间的累积生存期。

Kaplan-Meier图 

建立在上ggplot2，并可用于创建Kaplan-Meier图。

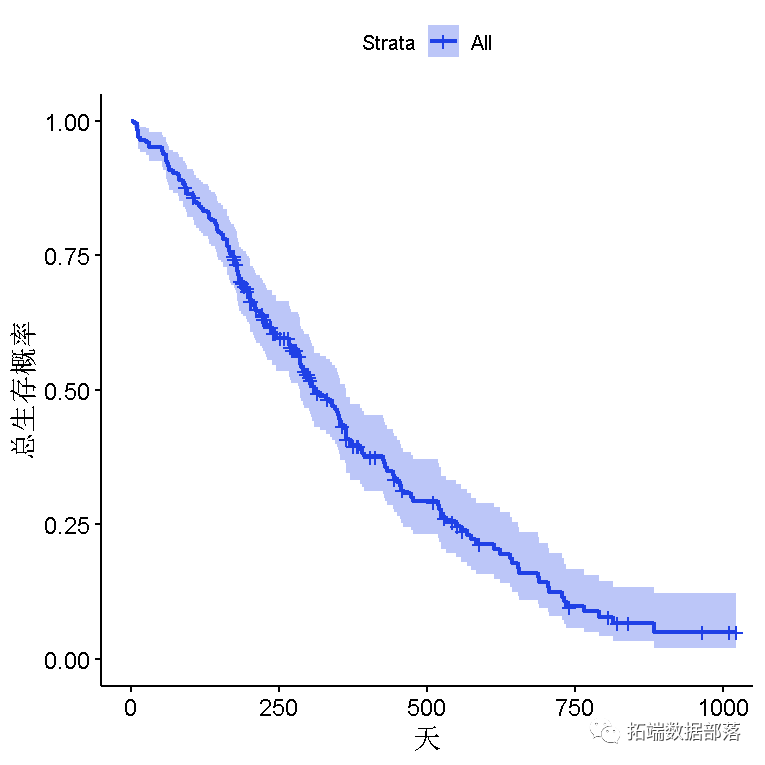
• 默认图  带相关置信带（阴影区域）的阶跃函数（实线）。

• 默认情况下，显示了被检查患者的刻度线，在此示例中，该刻度线本身有些模糊，可以使用选项将其取消 censor = FALSE

估计xx年生存

生存分析中经常需要关注的一个数量是生存超过一定数量（xx）年的概率。

例如，要估算生存到11年的可能性

1.  
   ## Call: survfit(formula = Surv(time, status) ~ 1, data = lung)
2.  
   ## 
3.  
   ##  time n.risk n.event survival std.err lower 95% CI upper 95% CI
4.  
   ##   365     65     121    0.409  0.0358        0.345        0.486

我们发现本研究中11年生存的机率是41％。

同时显示95％置信区间的相关上下限。

xx年生存率和生存曲线

11年存活率概率为在y轴上的点对应于11一年x轴的生存曲线。

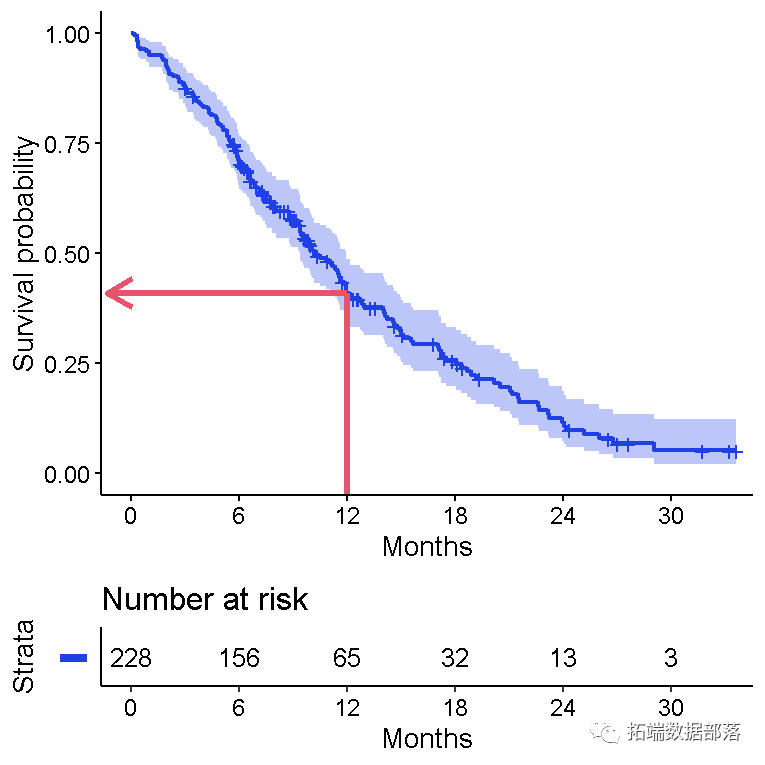
Xx年生存率常常被错误估计

如果 使用“天真”的估计会怎样？

228名患者中的121名到1年时死亡，因此：

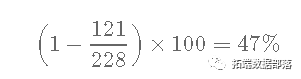
-当 忽略42名患者在1年之前受到检查的事实时， 会错误估计1个1个年生存率。

• 正确的估计生存概率-年为41％。

忽略删失对xx年生存的影响

• 想象两个研究，每个研究228个主题。每个研究中有165人死亡。一个没有检查（红色线），63个病人被另一个（蓝色线）检查

• 忽略删失会导致总体生存概率被高估，因为被删失的受试者仅在部分随访时间内提供信息，然后落入风险范围之外，从而降低了生存的累积概率

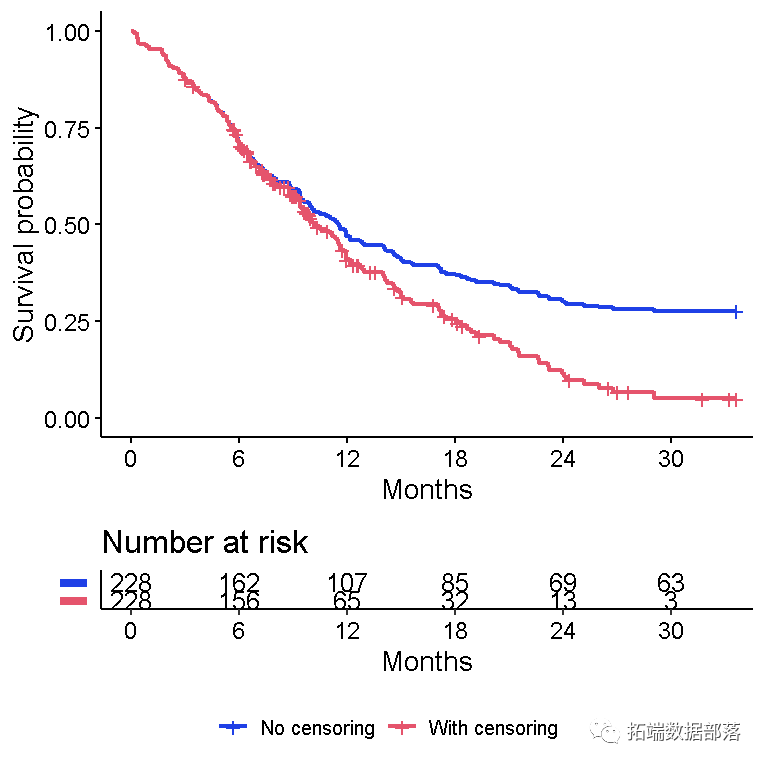
估计中位生存时间

生存分析中经常需要关注的另一个数量是平均生存时间，我们使用中位数对其进行量化。预计生存时间不会呈正态分布，因此平均值不是适当的总结。

1.  
   ## Call: survfit(formula = Surv(time, status) ~ 1, data = lung)
2.  
   ## 
3.  
   ##       n  events  median 0.95LCL 0.95UCL 
4.  
   ##     228     165     310     285     363

我们看到中位生存时间为310天。还会显示95％置信区间的上限和下限。

中位生存时间和生存曲线

中位生存时间是生存概率为0.50 

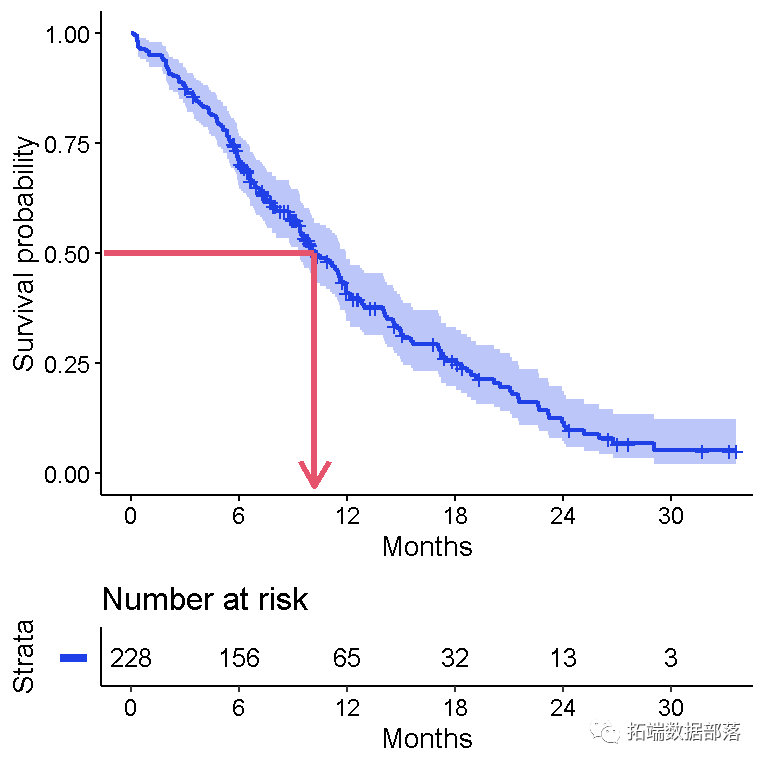
中位生存率常常被错误估计

总结165例死亡患者的中位生存时间

1.  
   ##   median_surv
2.  
   ## 1         226

• 当 忽略被检查患者也有助于随访的事实时， 会得出错误的估计中值生存时间226天。

• 正确的中位生存时间估计是310天。

忽略删失对中位数生存率的影响

• 忽略删失会造成人为降低的生存曲线，因为排除了受删失患者贡献的随访时间（紫色线）

• 数据的真实生存曲线以lung蓝色显示，以进行比较

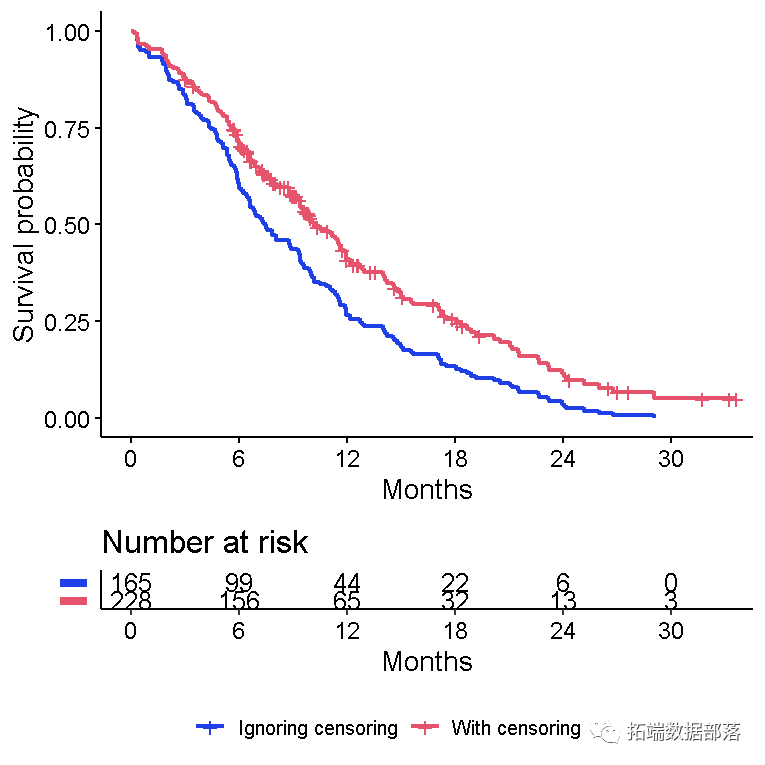
比较各组之间的生存时间

• 我们可以使用对数秩检验进行组间重要性检验

• 对数秩检验在整个随访时间内平均权衡观察结果，是比较组间生存时间的最常用方法

• 根据研究问题，有些版本可能会更重视早期或后期的随访，可能更合适

我们使用 函数获得对数秩p值。例如，我们可以根据lung数据中的性别测试是否存在生存时间差异

1.  
   ## Call:
2.  
   ## 
3.  
   ##         N Observed Expected (O-E)^2/E (O-E)^2/V
4.  
   ## sex=1 138      112     91.6      4.55      10.3
5.  
   ## sex=2  90       53     73.4      5.68      10.3
6.  
   ## 
7.  
   ##  Chisq= 10.3  on 1 degrees of freedom, p= 0.001

从survdiff对象中提取信息

从 结果中提取p值

1 - pchisq(sd$chisq, length(sd$n) - 1)

## \[1\] 0.001311165

返回格式化的p值

## \[1\] 0.001

Cox回归模型

我们可能想量化单个变量的效应大小，或者将多个变量包括在回归模型中以说明多个变量的效应。

Cox回归模型是半参数模型，可用于拟合具有生存结果的单变量和多变量回归模型。

h(t)h(t)：危险或事件发生的瞬时速率h0(t)h0(t)：基本基准危险

该模型的一些关键假设：

• 非信息删失

• 比例危险

_注意_：也可以使用用于生存结果的参数回归模型，但是本培训将不涉及这些模型。

我们可以使用coxph函数拟合生存数据的回归模型，该函数Surv在左侧使用一个对象，而在右侧具有用于回归公式的标准语法R。

1.  
   ## Call:
2.  
   ## 
3.  
   ##        coef exp(coef) se(coef)      z       p
4.  
   ## sex -0.5310    0.5880   0.1672 -3.176 0.00149
5.  
   ## 
6.  
   ## Likelihood ratio test=10.63  on 1 df, p=0.001111
7.  
   ## n= 228, number of events= 165

格式化Cox回归结果

我们可以看到输出的整洁版本broom：

或使用

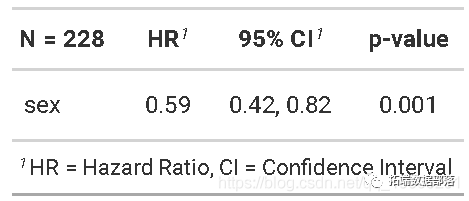
危险比

• 来自Cox回归模型的关注数量是危险比（HR）。HR表示在任何特定时间点两组之间的危险比率。

• HR被解释为感兴趣事件中那些仍处于事件风险中的事件的瞬时发生率。

• 如果您有一个回归参数ββ（来自estimate我们的列coxph），则HR = 经验值（β）经验值⁡（β）。

• HR <1表示死亡危险降低，而HR> 1表示死亡危险增加。

• 因此，我们的HR = 0.59意味着在任何给定时间，女性死亡的人数大约是男性的0.6倍。

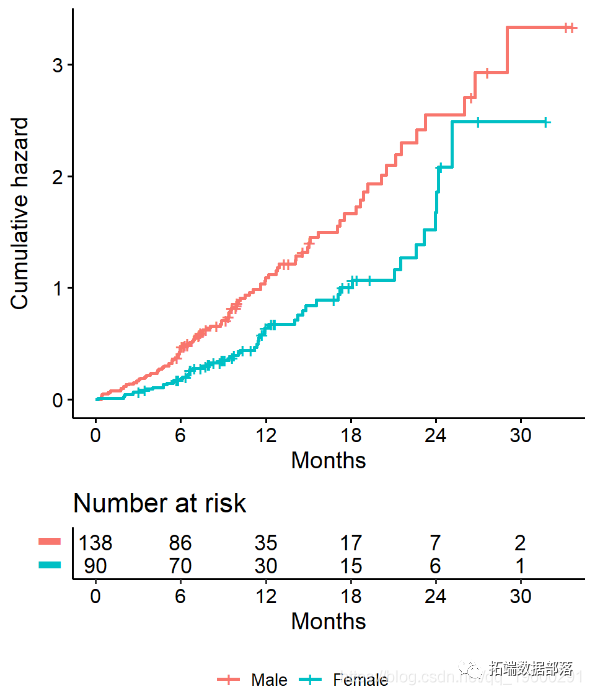
第2部分：地标分析和时间相关协变量

在第1部分中，我们介绍了使用对数秩检验和Cox回归来检验感兴趣的协变量与生存结果之间的关联。

示例：肿瘤反应

示例：从治疗开始就测量总生存期，关注的是对治疗的完全反应与生存之间的关联。

• Anderson等人（JCO，1983）描述了在这种情况下，为什么传统方法（如对数秩检验或Cox回归）偏向于响应者，并提出了划时代的方法。

• 界标方法中的零假设是，从界标生存的过程不依赖于界标的响应状态。

Anderson, J., Cain, K., & Gelber, R. (1983). Analysis of survival by tumor response. Journal of Clinical Oncology : Official Journal of the American Society of Clinical Oncology, 1(11), 710-9.

其他例子

癌症研究中可能尚未关注的其他一些可能的协变量包括：

• 移植失败

• 移植物抗宿主病

• 第二次切除

• 辅助治疗

• 合规

• 不良事件

示例数据 

137例骨髓移植患者的数据。变量包括：

• T1 死亡时间或最后一次随访时间（天）

• delta1死亡指标；1死0活

• TA 急性移植物抗宿主病的时间（以天为单位）

• deltaA急性移植物抗宿主病指标；1-发展为急性移植物抗宿主病，0-从未发展为急性移植物抗宿主病

让我们加载数据以供整个示例使用

地标法

1. 选择基线之后的固定时间作为界标时间。_注意_：应在检查数据之前根据临床信息进行操作

2. 那些人群的子集至少跟踪到里程碑时间。_注意_：请务必在地标时间之前报告由于关注或删失事件而排除的号码。

3. 计算具有里程碑意义的时间，并应用传统的对数秩检验或Cox回归

在BMT数据感兴趣的是急性移植物抗宿主病（aGVHD）和存活之间的关联。但是aGVHD是在移植后进行评估的，这是我们的基线，也就是后续随访的开始时间。

步骤1选择地标时间

通常，aGVHD发生在移植后的前90天内，因此我们使用90天的界标。

人们对急性移植物抗宿主病（aGVHD）与生存之间的关系感兴趣。但是aGVHD是在移植后进行评估的，这是我们的基线，也就是后续随访的开始时间。

第2步：至少跟踪到里程碑时间之前的人群的子集

这将我们的样本量从137减少到122。

• 所有15位被排除的患者均在90天里程碑之前死亡

人们对急性移植物抗宿主病（aGVHD）与生存之间的关系感兴趣。但是aGVHD是在移植后进行评估的，这是我们的基线，也就是后续随访的开始时间。

步骤3根据地标计算随访时间，并应用传统方法。

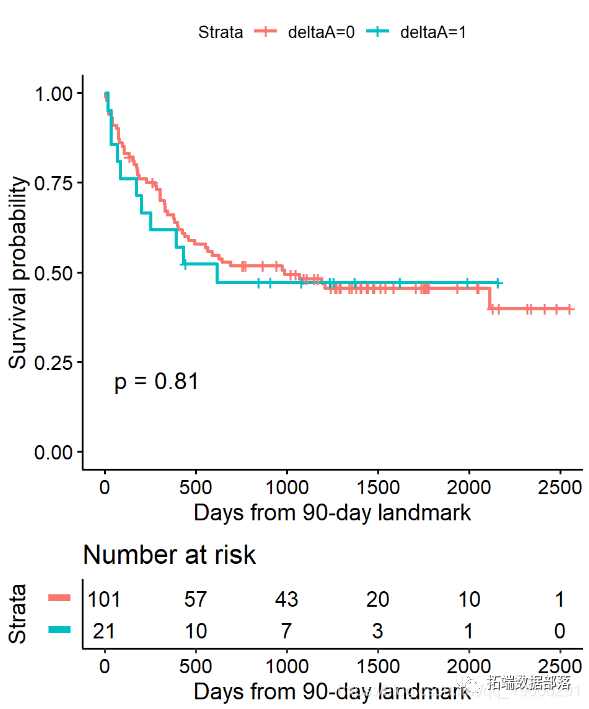
使用BMT数据的Cox回归界标示例

在Cox回归中， 可以使用中的subset选项coxph来排除那些在标志性时间内没有被随访的患者

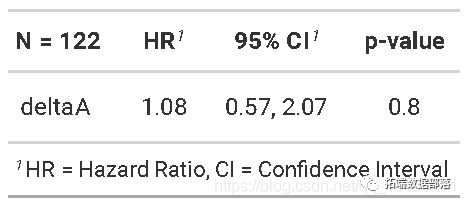
时间相关协变量

界标分析的替代方法是合并时间相关的协变量。这可能更适合

• 协变量的值随时间变化

• 没有明显的里程碑时间

时间相关协变量数据设置

对时间相关协变量的分析R需要建立特殊的数据集。 

BMT数据中没有ID变量，这是创建特殊数据集所必需的，因此请创建一个名为的变量my_id。

将tmerge函数与event和函数一起使用tdc可创建特殊数据集。

• tmerge 为每个患者的不同协变量值创建一个具有多个时间间隔的长数据集

• event 创建新的事件指示器，以与新创建的时间间隔一致

• tdc 创建与时间相关的协变量指标，以与新创建的时间间隔一致

时间相关协变量-单例患者

要了解其作用，让我们看一下前5名患者的数据。

1.  
    ##   my_id   T1 delta1   TA deltaA
2.  
   ## 1     1 2081      0   67      1
3.  
   ## 2     2 1602      0 1602      0
4.  
   ## 3     3 1496      0 1496      0
5.  
   ## 4     4 1462      0   70      1
6.  
   ## 5     5 1433      0 1433      0

这些相同患者的新数据集

1.  
   ##   my_id   T1 delta1 id tstart tstop death agvhd
2.  
   ## 1     1 2081      0  1      0    67     0     0
3.  
   ## 2     1 2081      0  1     67  2081     0     1
4.  
   ## 3     2 1602      0  2      0  1602     0     0
5.  
   ## 4     3 1496      0  3      0  1496     0     0
6.  
   ## 5     4 1462      0  4      0    70     0     0
7.  
   ## 6     4 1462      0  4     70  1462     0     1
8.  
   ## 7     5 1433      0  5      0  1433     0     0

时间相关协变量-Cox回归

现在，我们可以分析这个时间依赖性协照常使用Cox回归与coxph 

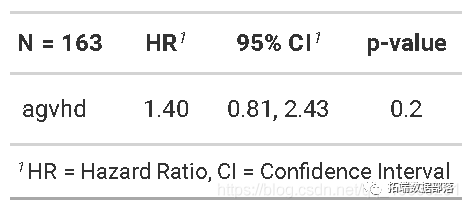
摘要

我们发现，使用标志性分析或时间依赖性协变量，急性移植物抗宿主病与死亡无显着相关性。

通常，人们会希望使用地标分析对单个协变量进行可视化， 使用带有时间相关协变量的Cox回归进行单变量和多变量建模。

第3部分：竞争风险

什么是竞争风险？

当对象在事件发生时间设置中发生多个可能的事件时

例子：

• 复发

• 因疾病死亡

• 因其他原因死亡

• 治疗反应

在任何给定的研究中，所有这些（或其中一些 以及其他）可能都是可能的事件。

所以有什么问题？

事件时间之间未观察到的依赖性是导致需要特殊考虑的基本问题。

例如，可以想象复发的患者更有可能死亡，因此复发时间和死亡时间将不是独立事件。

竞争风险的背景

存在多种潜在结果时的两种分析方法：

1. 给定事件的特定于原因的危险：这表示未因其他事件而失败的事件中事件的每单位时间的发生率

2. 给定事件的累积发生率：这表示事件每单位时间的发生率以及竞争事件的影响

这些方法中的每一种都可能仅阐明数据的一个重要方面，而有可能使其他方面难以理解，因此所选的方法应取决于感兴趣的问题。

 黑色素瘤数据示例

它包含变量：

• time 生存时间以天为单位，可能经过删失。

• status 1例死于黑色素瘤，2例存活，3例因其他原因死亡。

• sex 1 =男性，0 =女性。

• age 年岁。

• year 操作。

• thickness 肿瘤厚度（毫米）。

• ulcer 1 =存在，0 =不存在。

黑色素瘤数据的累积发生率

在竞争风险的背景下估算累积发生率。

1.  
   ## Estimates and Variances:
2.  
   ## $est
3.  
   ##           1000       2000       3000      4000      5000
4.  
   ## 1 1 0.12745714 0.23013963 0.30962017 0.3387175 0.3387175
5.  
   ## 1 3 0.03426709 0.05045644 0.05811143 0.1059471 0.1059471
6.  
   ## 
7.  
   ## $var
8.  
   ##             1000         2000         3000        4000        5000
9.  
   ## 1 1 0.0005481186 0.0009001172 0.0013789328 0.001690760 0.001690760
10.  
    ## 1 3 0.0001628354 0.0002451319 0.0002998642 0.001040155 0.001040155

绘制累积发生率-基数R

生成 默认值的基本图。

plot(ci_fit)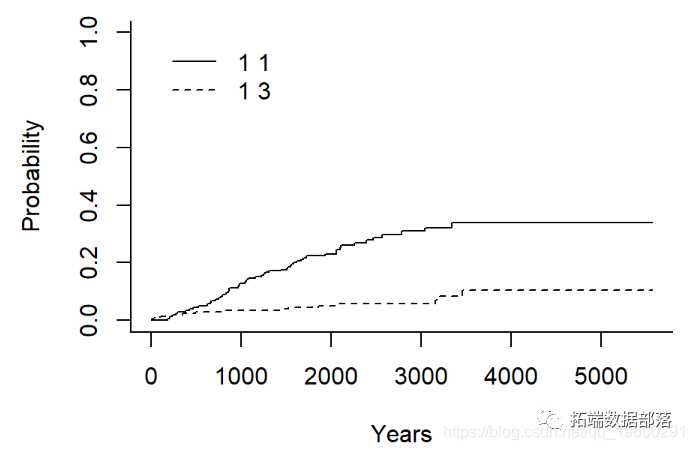

绘制累积发生率 

• 

比较组之间的累积发生率

用于组间测试。

例如，Melanoma根据ulcer溃疡的存在与否比较结果。测试结果可以在中找到Tests。

ci_ulcer\[\["Tests"\]\]

1.  
   ##        stat           pv df
2.  
   ## 1 26.120719 3.207240e-07  1
3.  
   ## 3  0.158662 6.903913e-01  1

按组绘制累积发生率 

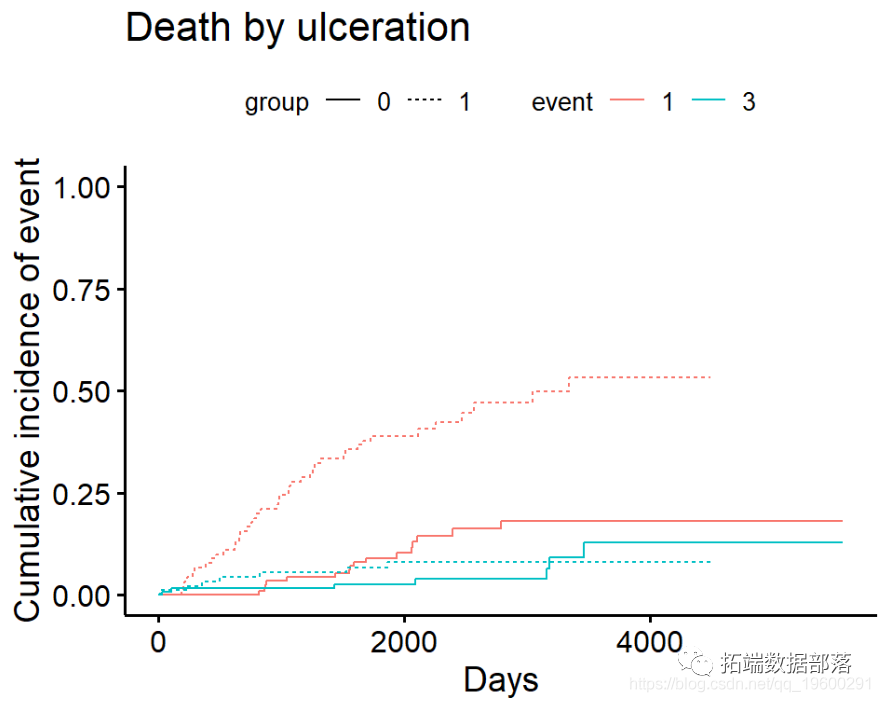
按组绘制累积发生率-手动

_请注意，_我个人发现该ggcompetingrisks功能缺少自定义功能，尤其是与相比ggsurvplot。我通常会自己做图，首先创建cuminc拟合结果的整洁数据集，然后再绘制结果。有关底层代码的详细信息，请参见此演示文稿的

绘制单个事件类型 

通常，只有一种类型的事件会引起人们的兴趣，尽管我们仍要考虑竞争事件。在那种情况下，感兴趣的事件可以单独绘制。同样，我首先通过创建cuminc拟合结果的整洁数据集，然后绘制结果来手动执行此操作。有关底层代码的详细信息，请参见此演示文稿的源代码。

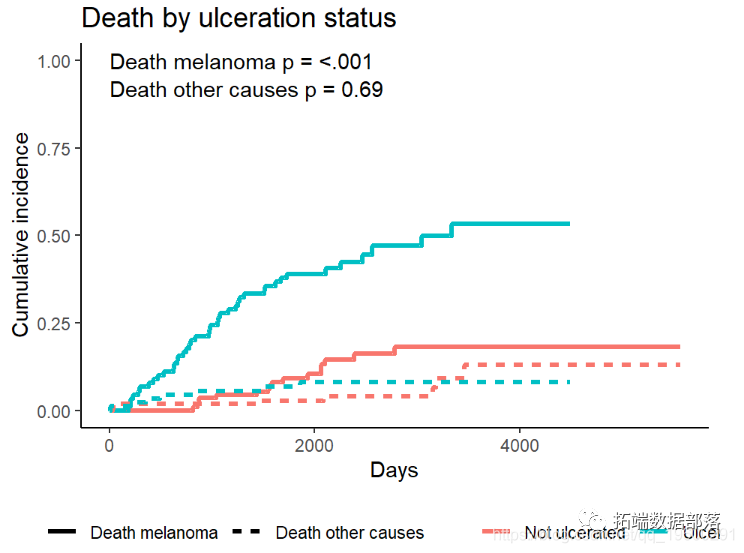
在风险表中添加数字

您可能想将风险表的数量添加到累积发生率图中，而据我所知，没有简单的方法可以做到这一点。请参阅此演示文稿的源代码中的一个示例

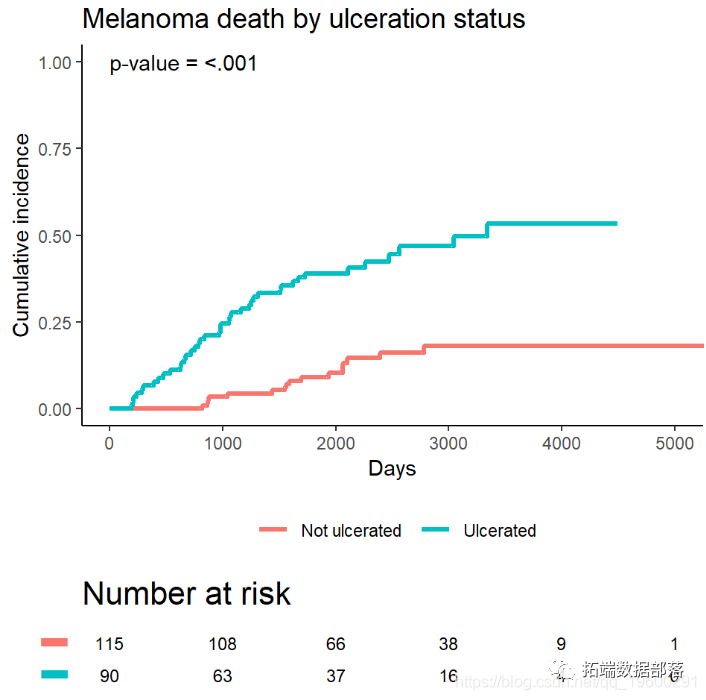
竞争风险回归

两种方法：

1. 特定原因风险

• 当前没有事件的受试者中给定事件类型的瞬时发生率

• 使用Cox回归估算

1. Subdistribution子分布风险

• 给定类型事件在没有经历过此类事件的受试者中的瞬时发生率

• 使用Fine-Gray回归估算

黑色素瘤数据中的竞争风险回归-子分布风险法Subdistribution

假设我们有兴趣研究年龄和性别对黑色素瘤死亡的影响，而其他原因的死亡则是竞争事件。

• crr 需要指定协变量作为矩阵

• 如果 关注多个事件，则可以使用failcode选项请求其他事件的结果，默认情况下会返回failcode = 1

shr_fit

1.  
   ## convergence:  TRUE 
2.  
   ## coefficients:
3.  
   ##     sex     age 
4.  
   ## 0.58840 0.01259 
5.  
   ## standard errors:
6.  
   ## \[1\] 0.271800 0.009301
7.  
   ## two-sided p-values:
8.  
   ##  sex  age 
9.  
   ## 0.03 0.18

在上一个示例中，sex和和age均被编码为数字变量。如果存在字符变量，则必须使用model.matrix

格式化来自crr的结果

或当前crr不支持的输出。 

黑色素瘤数据中的竞争风险回归-因果分析

删失所有没有引起关注的对象，在这种情况下是由于黑色素瘤死亡，并且照常使用coxph。因此，现在对因其他原因死亡的患者进行针对特定原因的风险评估方法以应对竞争风险。

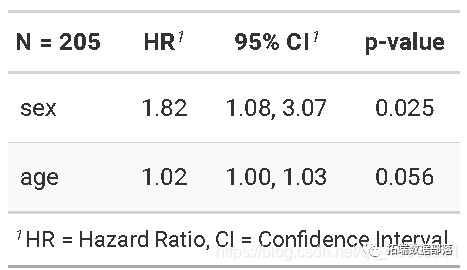
第4部分：高级主题

 涵盖的内容

• 生存分析的基础知识，包括Kaplan-Meier生存函数和Cox回归

• 地标分析和时间相关协变量

• 竞争风险分析的累积发生率和回归

还有什么？

可能会出现很多零碎的东西 ：

1. 评估比例风险假设

2. 生存率绘制平滑的生存图XX

3. 有条件的生存

评估比例风险

Cox比例风险回归模型的一个假设是，在整个随访过程中，风险在每个时间点都是成比例的。我们如何检查数据是否符合此假设？

使用cox.zph生存包中的功能。结果有两点：

1. 每个协变量的效果是否随时间变化的假设检验，以及一次所有协变量的全局检验。

• 这是通过证明协变量和log（time）之间的交互作用来完成的

• 显着的p值表示违反了比例风险假设

1. Schoenfeld残差图

• 偏离零坡度线的证据表明违反了比例风险假设

print(cz)

1.  
   ##            rho chisq     p
2.  
   ## sex     0.1236 2.452 0.117
3.  
   ## age    -0.0275 0.129 0.719
4.  
   ## GLOBAL      NA 2.651 0.266
5.  
   ``````
6.  
   plot(cz)

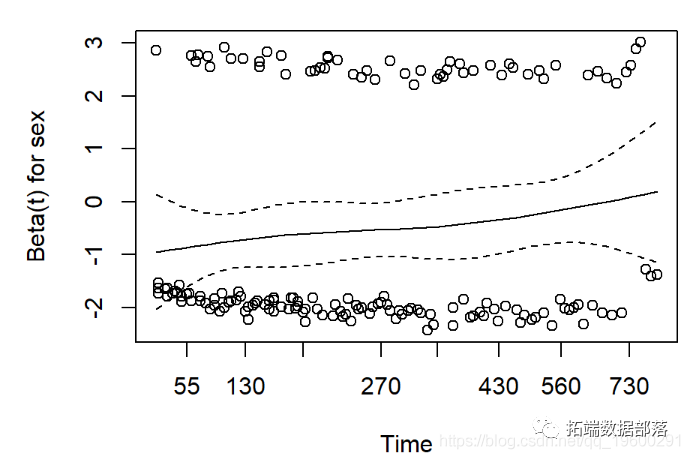
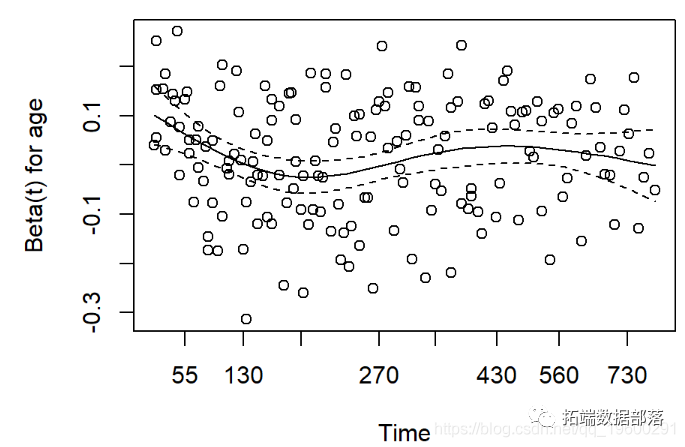
平滑的生存图-生存分位数

有时可能想根据连续变量来可视化生存估计。求 生存数据的分位数。默认分位数是p = 0.5中位生存期。

• x代表事件

• o代表删失

• 该线是根据年龄的平均存活率的平滑估计

• 

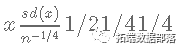
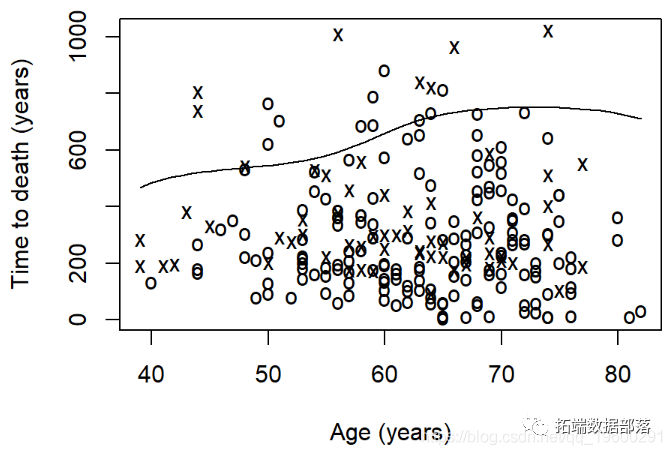
条件生存

有时，在已经存活了一段时间的患者中产生存活率估计值很有意义。

Zabor, E., Gonen, M., Chapman, P., & Panageas, K. (2013). Dynamic prognostication using conditional survival estimates. Cancer, 119(20), 3589-3592.

条件生存估计

让我们将生存期定为6个月

1.  
   map_df(
2.  
     prob_times, 
3.  
     ~conditional\_surv\_est(
4.  
       basekm = fit1, 
5.  
       t1 = 182.625, 
6.  
       t2 = .x) 
7.  
     ) %>% 
8.  
     mutate(months = round(prob_times / 30.4)) %>% 
9.  
     select(months, everything()) %>% 
10.  
      kable()

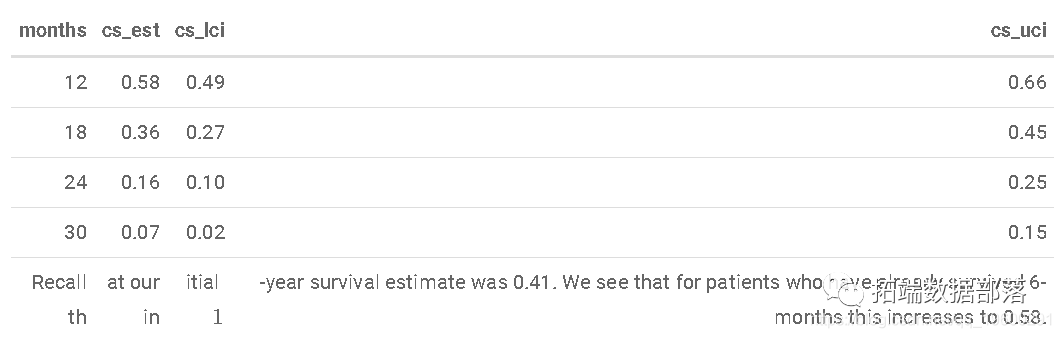
条件生存图

我们还可以根据不同的生存时间长度可视化条件生存数据。 

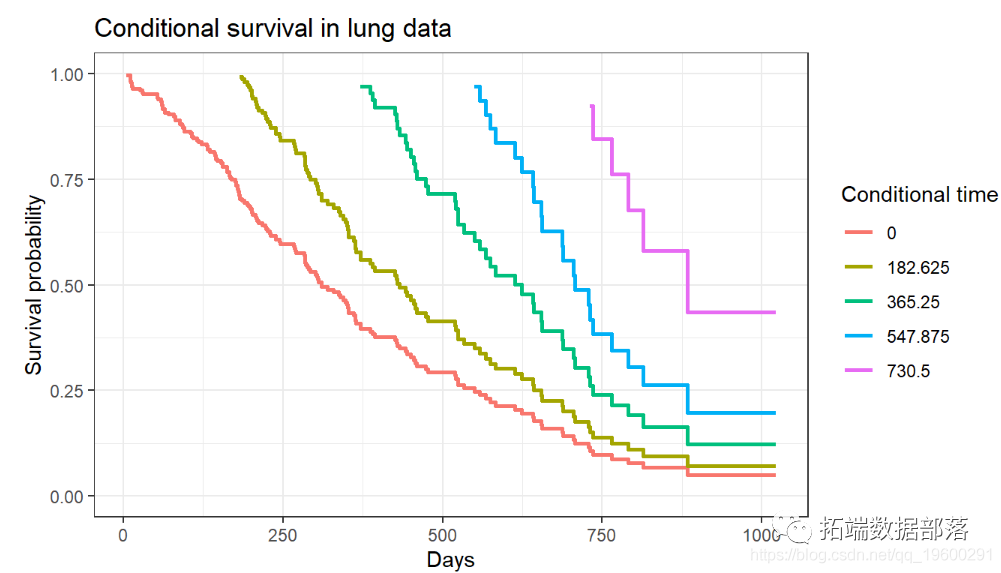
所得出的曲线在我们每次进行条件调整时都有一条生存曲线。在这种情况下，第一条线是总体生存曲线，因为它是根据时间0进行调节的。

数据获取

在下面公众号后台回复“肺癌数据”，可获取完整数据。