原文链接:http://tecdat.cn/?p=24814
原文出处:拓端数据部落公众号
说到在股票市场上赚钱,有无数种不同的赚钱方式。似乎在金融界,无论你走到哪里,人们都在告诉你应该学习 Python。毕竟,Python 是一种流行的编程语言,可用于所有类型的领域,包括数据科学。有大量软件包可以帮助您实现目标,许多公司使用 Python 来开发与金融界相关的以数据为中心的应用程序和科学计算。
最重要的是,Python 可以帮助我们利用许多不同的交易策略,这些策略(没有它)将很难用手或电子表格进行分析。我们将讨论的交易策略之一称为 配对交易。
配对交易
配对交易是均值回归的一种形式 ,具有始终对冲市场波动的独特优势。该策略基于数学分析。
原理如下。假设您有一对具有某种潜在经济联系的证券 X 和 Y。一个例子可能是生产相同产品的两家公司,或一条供应链中的两家公司。如果我们可以用数学模型对这种经济联系进行建模,我们就可以对其进行交易。
为了理解配对交易,我们需要理解三个数学概念: 平稳性、差分和协整。
-
import numpy as np
-
import pandas as pd
平稳/非平稳
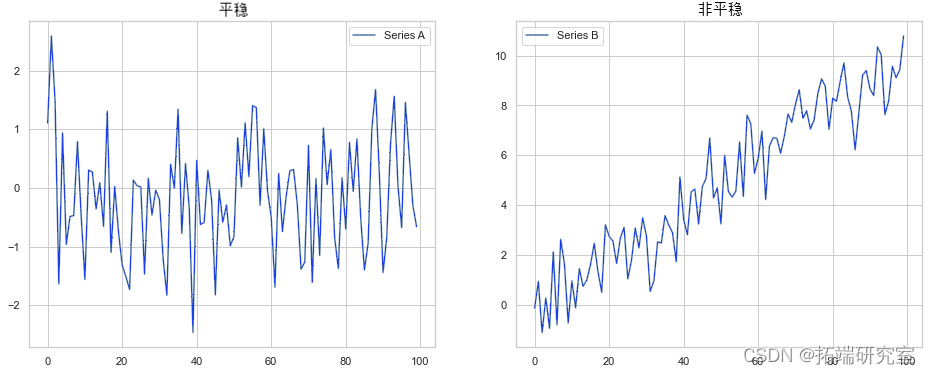
平稳性是时间序列分析中最常见的未经检验的假设。当数据生成过程的参数不随时间变化时,我们通常假设数据是平稳的。或者考虑两个系列:A 和 B。系列 A 将生成具有固定参数的平稳时间序列,而 B 将随时间变化。
我们将创建一个函数,为概率密度函数创建 z 分数。高斯分布的概率密度为:
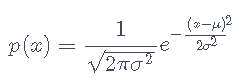
![]() 是均值和
是均值和 ![]() 是标准差。标准差的平方,
是标准差。标准差的平方, ![]() ,是方差。经验法则规定 66% 的数据应该介于
,是方差。经验法则规定 66% 的数据应该介于 ![]() 和
和 ![]() ,这意味着该函数
,这意味着该函数normal 更有可能返回靠近均值的样本,而不是那些远离均值的样本。
-
-
mu
-
sigma
-
return normal(mu, sigma )
从那里,我们可以创建两个展示平稳和非平稳时间序列的图。
-
-
# 设置参数和数据点数
-
T = 100
-
-
Series(index=range(T))
-
-
-
# 现在参数依赖于时间
-
# 具体来说,序列的均值随时间变化
-
B[t] = genedata
-
-
plt.subplots
为什么平稳性很重要
许多统计测试要求被测试的数据是平稳的。在非平稳数据集上使用某些统计数据可能会导致垃圾结果。作为一个例子,让我们通过我们的非平稳 ![]() .
.
-
np.mean
-
-
plt.figure
-
plt.plot
-
plt.hlines
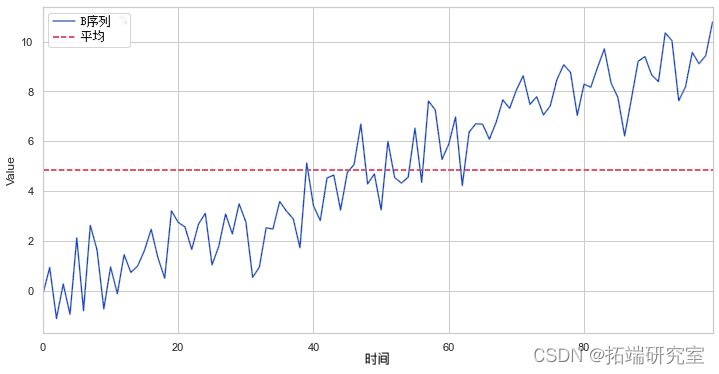
计算的平均值将显示所有数据点的平均值,但对未来状态的任何预测都没有用。与任何特定时间相比,它毫无意义,因为它是不同时间的不同状态混搭在一起的集合。这只是一个简单而清晰的例子,说明了为什么非平稳性会扭曲分析,在实践中会出现更微妙的问题。
平稳性检验Augmented Dickey Fuller(ADF)
为了测试平稳性,我们需要测试一个叫做单位根的东西 。自回归单位根检验基于以下假设检验:
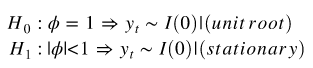
它被称为单位根 tet 因为在原假设下,自回归多项式 ![]() , 的根等于 1。
, 的根等于 1。![]() 在原假设下趋势平稳。如果
在原假设下趋势平稳。如果 ![]() 然后首先进行差分,它变成:
然后首先进行差分,它变成:
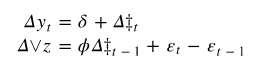
检验统计量为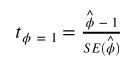
![]() 是最小二乘估计和 SE(
是最小二乘估计和 SE(![]() ) 是通常的标准误差估计。该测试是单侧左尾测试。如果 {undefined
) 是通常的标准误差估计。该测试是单侧左尾测试。如果 {undefined![]() } 是平稳的,那么可以证明
} 是平稳的,那么可以证明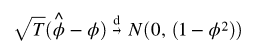 或者
或者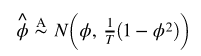 并且是
并且是 ![]() ,然而,在非平稳性原假设下,上述结果给出
,然而,在非平稳性原假设下,上述结果给出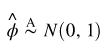 以下函数将允许我们使用 Augmented Dickey Fuller (ADF) 检验来检查平稳性。
以下函数将允许我们使用 Augmented Dickey Fuller (ADF) 检验来检查平稳性。
-
-
defty_test(X, cutoff=0.01):
-
# adfuller 中的 H_0 是单位根存在(非平稳)
-
# 我们必须观察显着的 p 值看该序列是平稳的
-
adfuller

正如我们所见,基于时间序列 A 的检验统计量(与特定的 p 值对应),我们可能无法拒绝原假设。因此,A 系列很可能是静止的。另一方面,B系列被假设检验拒绝,所以这个时间序列很可能是非平稳的。
协整
金融数量之间的相关性是出了名的不稳定。尽管如此,几乎所有的多元金融问题都经常使用相关性。相关性的另一种统计度量是协整。这可能是衡量两个金融数量之间联系的更稳健的衡量标准,但迄今为止,几乎没有基于此概念的偏差理论。
两只股票可能在短期内完全相关,但从长远来看却出现分歧,一只增长,另一只下跌。相反,两只股票可能相互跟随,相距不会超过一定距离,但具有相关性,正负相关变化。如果我们是短期,相关性可能很重要,但如果我们在投资组合中长期持有股票,则无关紧要。
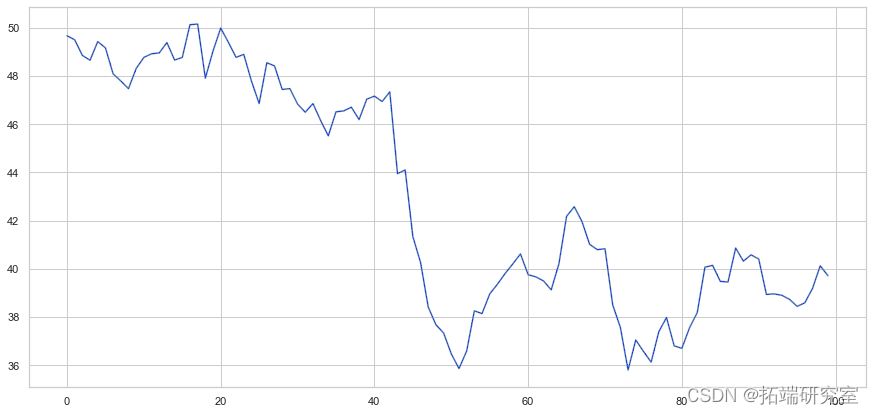
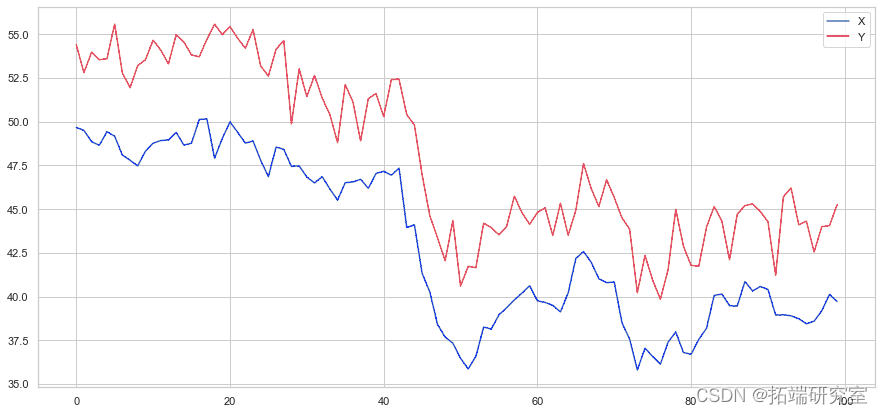
我们已经构建了两个协整序列的示例。我们现在绘制两者之间的差异。
-
-
# 生成每日收益
-
-
np.random.normal
-
-
# 总结
-
-
-
plot
-
-
np.random.normal
-
Y = X + 6 + 噪音
-
-
plt.show()
-
-
-
-
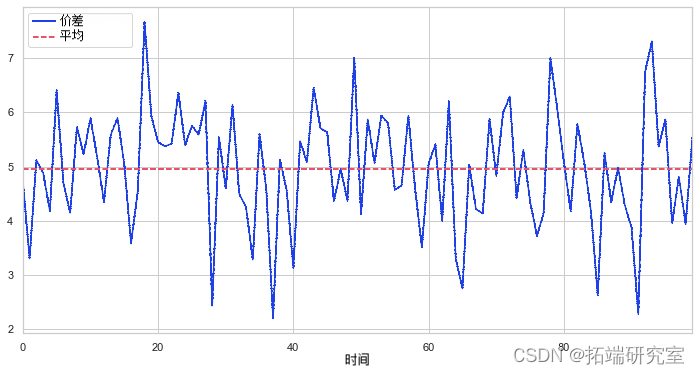
(Y - X).plot # 绘制点差
-
plt.axhline# 添加均值
-
plt.xlabel
-
plt.xlim
-
-
协整检验
协整检验程序的步骤:
-
检验每个分量系列的单位根
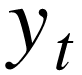 单独使用单变量单位根检验,例如 ADF、PP 检验。
单独使用单变量单位根检验,例如 ADF、PP 检验。 -
如果单位根不能被拒绝,那么下一步就是检验分量之间的协整关系,即检验是否
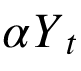 是 I(0)。
是 I(0)。
如果我们发现时间序列为单位根,那么我们继续进行协整过程。有三种主要的协整检验方法:Johansen、Engle-Granger 和 Phillips-Ouliaris。我们将主要使用 Engle-Granger 测试。
让我们考虑回归模型 ![]() :
:
![]() 中
中![]() 是确定性项。假设检验如下:
是确定性项。假设检验如下:
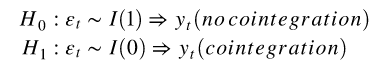
![]() 与 归一化的协整向量协整
与 归一化的协整向量协整
![]()
我们也使用残差 ![]() 用于单位根检验。
用于单位根检验。
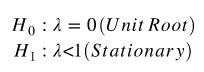
该假设检验适用于模型:
![]()
以下等式的检验统计量: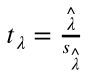
现在您了解了两个时间序列协整的含义,我们可以对其进行测试并使用 python 进行测量:
-
coint
-
print(pvalue)
-
-
-
# 低p值意味着高协整!
![]()
相关与协整
相关性和协整性虽然在理论上相似,但完全不同。为了证明这一点,我们可以查看两个相关但不协整的时间序列的示例。
一个简单的例子是两个序列。
-
Xruns = np.random.normal
-
yrurs = np.random.normal
-
-
-
-
pd.concat
-
plt.xlim
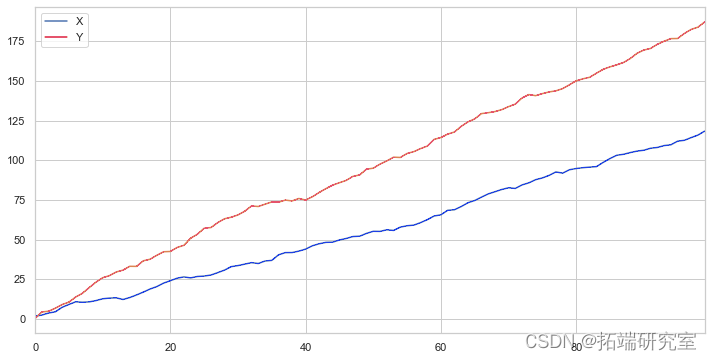
接下来,我们可以输出相关系数, ![]() , 和协整检验
, 和协整检验

正如我们所看到的,序列 X 和 Y 之间存在非常强的相关性。 然而,我们协整检验的 p 值产生了 0.7092,这意味着时间序列 X 和 Y 之间没有协整。
这种情况的另一个例子是正态分布系列和方波。
-
-
Y2 = pd.Series
-
-
-
-
plt.figure
-
Y2.plot()
-
-
# 相关性几乎为零
-
-
prinr(pvle))
-

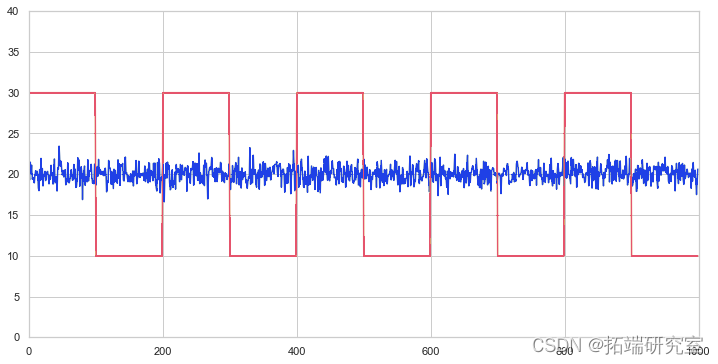
尽管相关性非常低,但 p 值表明这些时间序列是协整的。
-
-
import fix_yaance as yf
-
yf.pdrde
交易中的数据科学
在开始之前,我将首先定义一个函数,该函数可以使用我们已经涵盖的概念轻松找到协整对。
-
def fitirs(data):
-
n = data.shape
-
srmaix = np.zeros
-
pvl_mrix = np.ones
-
keys = dta.keys
-
for i in range(n):
-
for j in range:
-
-
reut = coint
-
sr = ret[0]
-
paue = rsult[1]
-
soeix[i, j] = score
-
pu_trix[i, j] = palue
-
if palue < 0.05:
-
pairs.append
-
return soe_mati, prs
我们正在查看一组科技公司,看看它们中是否有任何一家是协整的。我们将首先定义我们想要查看的证券列表。然后我们将获得 2013 - 2018 年每个证券的定价数据..
如前所述,我们已经制定了一个经济假设,即科技行业内的证券子集之间存在某种联系,我们想测试是否存在任何协整对。与搜索数百种证券相比,这产生的多重比较偏差要小得多,而比为单个测试形成假设的情况略多。
-
start = datetime.datetime
-
end = datetime.datetime
-
-
-
-
-
df = pdr(tcrs, strt, nd)['Close']
-
df.tail()

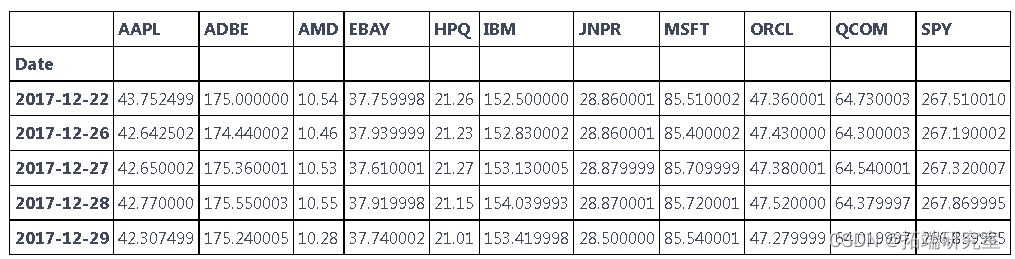
-
-
# 热图显示每对之间的协整检验的 p 值股票。 只显示热图上对角线上的值
-
分数、
-
-
seaborn.heatmap
-
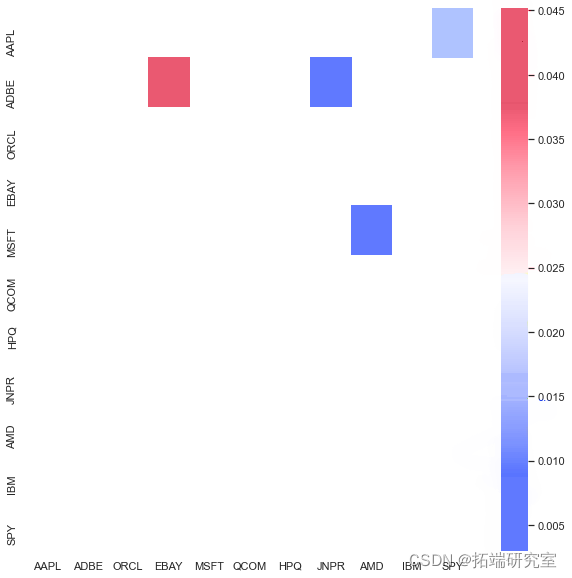
我们的算法列出了两个协整对:AAPL/EBAY 和 ABDE/MSFT。我们可以分析他们的模式。
-
-
coit
-
pvalue
![]()
如我们所见,p 值小于 0.05,这意味着 ADBE 和 MSFT 确实是协整对。
计算价差
现在我们可以绘制这两个时间序列的价差。为了实际计算价差,我们使用线性回归来获得我们两个证券之间的线性组合的系数,正如之前提到的恩格尔-格兰杰方法。
-
results.params
-
-
sed = S2 - b * S1
-
sedplot
-
plt.axhline
-
plt.xlim
-
plt.legend
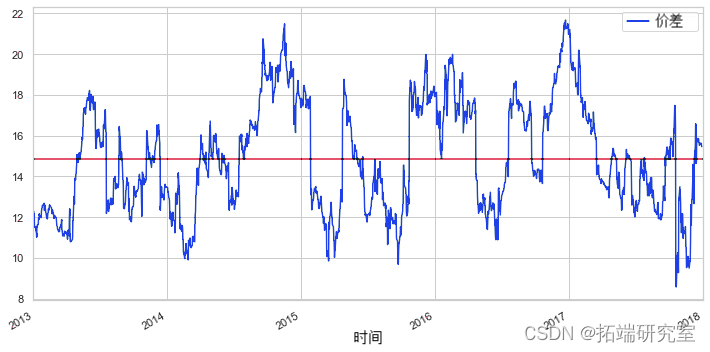
或者,我们可以检查两个时间序列之间的比率
-
rio
-
rao.plot
-
plt.axhline
-
plt.xlim
-
plt.legend
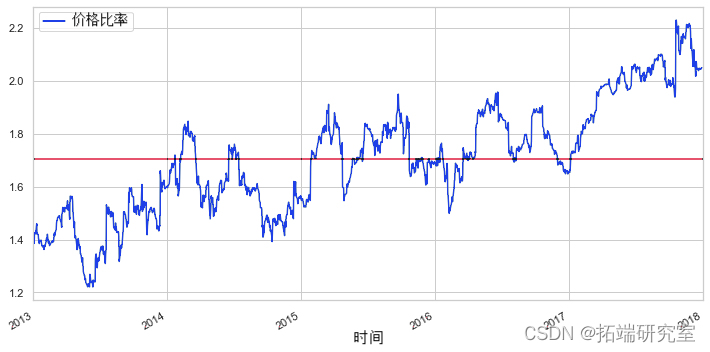
无论我们是使用价差法还是比率法,我们都可以看到我们的第一个图对 ADBE/SYMC 倾向于围绕均值移动。我们现在需要标准化这个比率,因为绝对比率可能不是分析这种趋势的最理想方式。为此,我们需要使用 z 分数。
z 分数是数据点与平均值的标准差数。更重要的是,高于或低于总体平均值的标准差的数量来自原始分数。z-score 的计算方法如下:
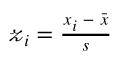
-
def zscr:
-
return (sres - ees.mean) / np.std
-
-
-
zscr.plot
-
plt.axhline
-
plt.axhline
-
plt.axhline
-
plt.xlim
-
plt.show
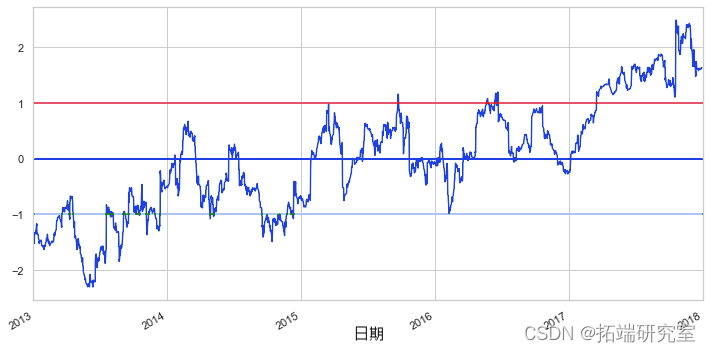
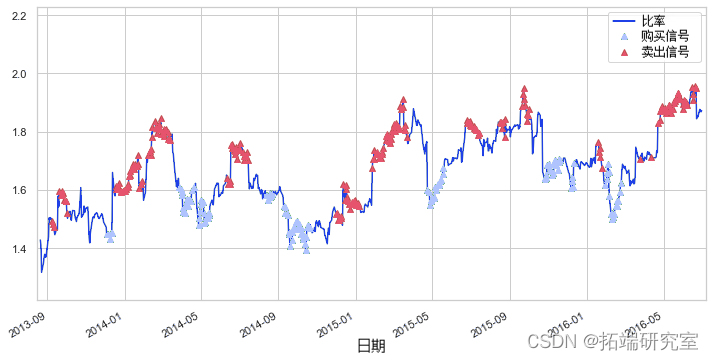
通过将另外两条线放置在 z 分数 1 和 -1 处,我们可以清楚地看到,在大多数情况下,与平均值的任何大背离最终都会收敛。这正是我们想要的配对交易策略。
交易信号
在进行任何类型的交易策略时,明确定义和描述实际进行交易的时间点总是很重要的。例如,我需要买卖特定股票的最佳指标是什么?
设置规则
我们将使用我们创建的比率时间序列来查看它是否告诉我们是在特定时间买入还是卖出。我们将首先创建一个预测变量 ![]() . 如果比率为正,则表示“买入”,否则表示卖出。预测模型如下:
. 如果比率为正,则表示“买入”,否则表示卖出。预测模型如下:
![]()
配对交易信号的好处在于,我们不需要知道价格将走向的绝对信息,我们只需要知道它的走向:上涨或下跌。
训练测试拆分
在训练和测试模型时,通常会有 70/30 或 80/20 的分割。我们只使用了 252 个点的时间序列(这是一年中的交易天数)。在训练和拆分数据之前,我们将在每个时间序列中添加更多数据点。
-
ratios = df['ADBE'] / df['MSFT']
-
print(len(ratios) * .70 )
![]()
-
tran = ratos[:881]
-
tet = rats[881:]
特征工程
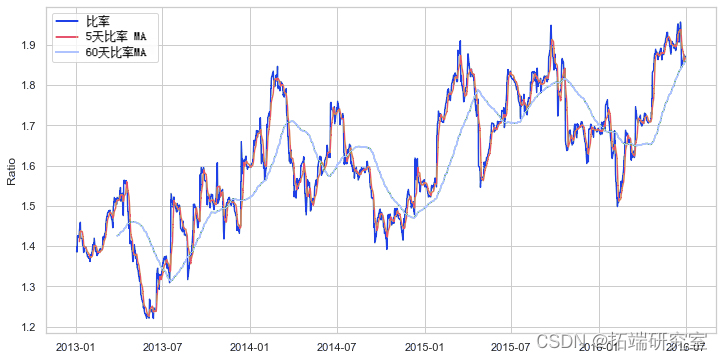
我们需要找出哪些特征在确定比率移动的方向上实际上很重要。知道比率最终总是会恢复到均值,也许与均值相关的移动平均线和指标将很重要。
让我们尝试:
-
60 天移动平均线
-
5 天移动平均线
-
60 天标准差
-
z 分数
-
train.rolg
-
zcoe_5 = (ra_ag5 - rasag60)/
-
plt.figure
-
plt.plot
-
plt.legend
-
plt.ylabel
-
plt.show
-
plt.figure
-
z5.plot()
-
plt.xlim
-
plt.axhline
-
plt.legend
-
plt.show
创建模型
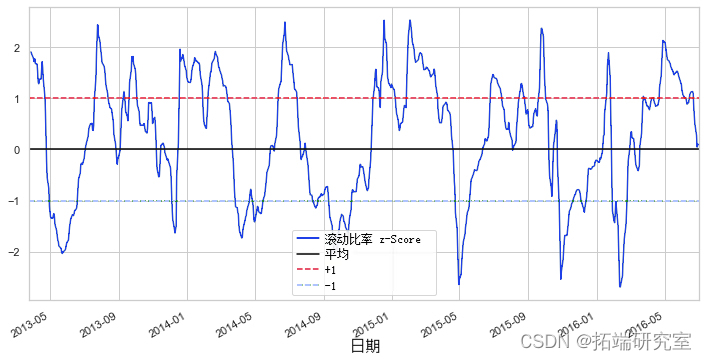
标准正态分布的均值为 0,标准差为 1。从图中可以看出,很明显,如果时间序列超出均值 1 个标准差,则趋向于恢复到均值。使用这些模型,我们可以创建以下交易信号:
-
每当 z-score 低于 -1 时, 买入(1),这意味着我们预计比率会增加。
-
每当 z 得分高于 1 时,卖出(-1),这意味着我们预计比率会下降。
训练优化
我们可以在实际数据上使用我们的模型
-
-
train.plot()
-
buy
-
sell
-
buy[z>-1] = 0
-
sell[z5<1] = 0
-
buy[160:].plot
-
sell[160:].plot
-
plt.figure
-
-
-
# 当您买入比率时,您买入股票 S1 并卖出 S2
-
-
sell[buy!=0] = S[uy!=0]
-
-
# 当您卖出比率时,您卖出股票 S1 并买入 S2
-
-
sell[sll!=0] = S1[sll!=0]
-
-
BuR[60:].plot
-
selR[60:].plot
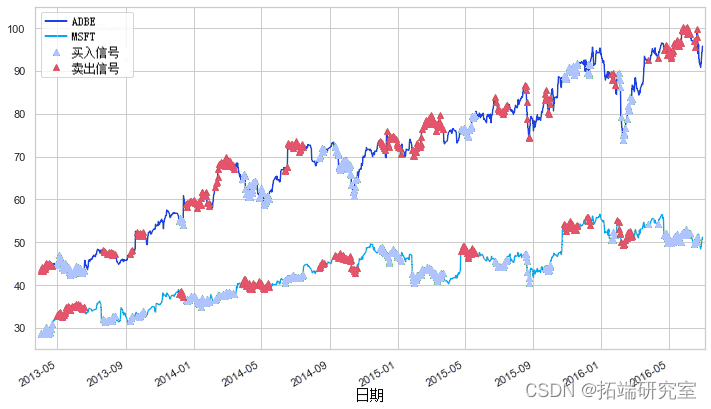
现在我们可以清楚地看到我们应该何时买入或卖出相应的股票。
现在,我们可以期望从这个策略中获得多少收益?
-
-
# 使用简单的 strydef 进行交易:
-
-
# 如果窗口长度为0,算法没有意义,退出
-
-
-
# 计算滚动平均值和滚动标准差
-
比率 = S1/S2
-
a1 = rais.rolng
-
zscoe = (ma1 - ma2)/std
-
-
# 模拟交易
-
-
# 对于范围内的 i(len(ratios)):
-
# 如果 z-score > 1,则卖空
-
-
mey += S1[i] - S2[i] * rts[i]
-
-
cutS2 += raos[i]
-
-
# 如果 z-score < -1,则买入多头
-
ef zoe[i] > 1:
-
mey -= S1[i] - S2[i] * rtos[i]
-
-
# 如果 z-score 介于 -.5 和 .5 之间,则清除
-
elif abs(zcre[i]) < 0.75:
-
mey += S1[i] * ctS + S2[i] * oS2
-
trad
![]()
对于从策略制定的策略来说,这是一个不错的利润。
改进的领域和进一步的步骤
这绝不是一个完美的战略,我们战略的实施也不是最好的。但是,有几件事可以改进。
1. 使用更多的证券和更多样化的时间范围
对于配对交易策略的协整测试,我只使用了少数股票。自然地(并且在实践中)在行业内使用集群会更有效。我只用了只有5年的时间范围,这可能不能代表股市的波动。
2. 处理过拟合
任何与数据分析和训练模型相关的事情都与过拟合问题有很大关系。有许多不同的方法可以处理像验证这样的过拟合,例如卡尔曼滤波器和其他统计方法。
3. 调整交易信号
我们的交易算法没有考虑到相互重叠和交叉的股票价格。考虑到该代码仅根据其比率要求买入或卖出,它并未考虑实际上哪个股票更高或更低。
4. 更高级的方法
这只是算法对交易的冰山一角。这很简单,因为它只处理移动平均线和比率。如果您想使用更复杂的统计数据,请使用。其他复杂示例包括 Hurst 指数、半衰期均值回归和卡尔曼滤波器等主题。
最受欢迎的见解
1.R语言对S&P500股票指数进行ARIMA + GARCH交易策略
2.R语言改进的股票配对交易策略分析SPY—TLT组合和中国股市投资组合
3.R语言时间序列:ARIMA GARCH模型的交易策略在外汇市场预测应用