P3355 骑士共存问题

P3355 骑士共存问题

题目描述
在一个 n*n (n <= 200)个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

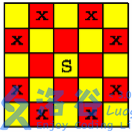
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

Solution

二分图最大独立集
骑士共存是这个的经典模型
两个点互相干涉的点只能取其一

定理： 二分图的最大独立集为其点数减去最大匹配数
证明：
最大独立集： 最多互不干涉的点
(Rightarrow) 选出最少的点使得剩下的互不干涉
(Rightarrow) 选出最多的点覆盖所有干涉边
而最小点覆盖 (=) 最大匹配数
故成立
证毕。

类似棋盘覆盖问题， 我们将棋盘黑白染色
发现此点与干涉点属于不同的颜色
故有干涉关系的连边做二分图最大匹配即可
此题卡匈牙利算法， 使用最大流

Code

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define LL long long
#define REP(i, x, y) for(int i = (x);i <= (y);i++)
using namespace std;
int RD(){
    int out = 0,flag = 1;char c = getchar();
    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
    return flag * out;
    }
const int maxn = 419, maxv = 1000019, INF = 1e9 + 19;
int head[maxn * maxn],nume = 1;
struct Node{
    int v,dis,nxt;
    }E[maxv << 3];
void add(int u,int v,int dis){
    E[++nume].nxt = head[u];
    E[nume].v = v;
    E[nume].dis = dis;
    head[u] = nume;
    }
int len, num;
int map[maxn][maxn];
int mx[8] = {-2,-1, 1, 2, 2, 1,-1,-2};
int my[8] = {-1,-2,-2,-1, 1, 2, 2, 1};
bool judge(int x, int y){
	if(x < 1 || x > len || y < 1 || y > len)return 0;
	return 1;
	}
int id(int x, int y){return (x - 1) * len + y;}
int s, t, maxflow;
int d[maxn * maxn];
bool bfs(){
	queue<int>Q;
	memset(d, 0, sizeof(d));
	d[s] = 1;
	Q.push(s);
	while(!Q.empty()){
		int u = Q.front();Q.pop();
		for(int i = head[u];i;i = E[i].nxt){
			int v = E[i].v;
			if(!d[v] && E[i].dis){
				d[v] = d[u] + 1;
				Q.push(v);
				if(v == t)return 1;
				}
			}
		}
	return 0;
	}
int Dinic(int u, int flow){
	if(u == t)return flow;
	int rest = flow, k;
	for(int i = head[u];i;i = E[i].nxt){
		int v = E[i].v;
		if(d[v] == d[u] + 1 && E[i].dis){
			k = Dinic(v, min(rest, E[i].dis));
			if(!k)d[v] = 0;
			E[i].dis -= k;
			E[i ^ 1].dis += k;
			rest -= k;
			if(!rest)break;
			}
		}
	return flow - rest;
	}
int main(){
	len = RD(), num = RD();
	s = 0, t = maxn * maxn - 19;
	REP(i, 1, num){
		int x = RD(), y = RD();
		map[x][y] = 1;
		}
	REP(i, 1, len)REP(j ,1, len){
		if(map[i][j])continue;
		int now = id(i, j);
		if((i + j) % 2 == 1)add(s, now, 1), add(now, s, 0);
		else add(now, t, 1), add(t, now, 0);
		}
	REP(i, 1, len)REP(j ,1, len){
		if(map[i][j] || (i + j) % 2 == 0)continue;
		int u = id(i ,j);
		for(int k = 0;k < 8;k++){
			int nx = i + mx[k];
			int ny = j + my[k];
			if(!judge(nx, ny))continue;
			if(map[nx][ny])continue;
			int v = id(nx, ny);
			add(u, v, 1), add(v, u, 0);
			}
		}
	int flow = 0;
	while(bfs())while(flow = Dinic(s, INF))maxflow += flow;
	printf("%d
",len * len - maxflow - num);
	return 0;
	}