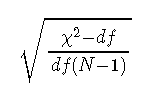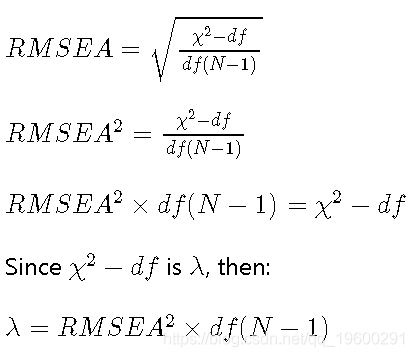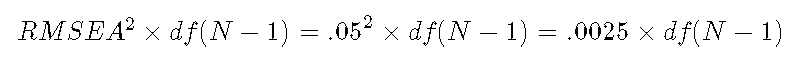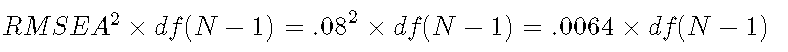R语言基于协方差的结构方程拟合的卡方检验

原文链接：http://tecdat.cn/?p=10426 

在评估结构方程模型的拟合，很常见的应用是研究χ2进行测试，因为在给定足够大的样本量的情况下，它几乎总会检测出模型与数据之间的统计上的显着差异。因为，我们的模型几乎总是数据的近似值。如果我们的模型的协方差矩阵实际上匹配抽样变异中的样本协方差矩阵，该χ2 无论样本量多大，该检验在统计学上均无统计学意义。

因为到大样本量，从业人员往往依赖于其他拟合指数，如RMSEA，CFI和TLI-所有这些都是基于χ 2。在lavaan中，您会自动使用置信区间和p值对RMSEA进行紧密拟合测试。这个测试实际上使用χ2分布。

RMSEA的公式为：

​

其中，χ2是χ2模型的检验统计量，dF是模型自由度，N是样本量。

如果你的模型拟合数据完美，分子为零；这是标准的假设χ 2χ2-test测试。如果我们在RMSEA进行测试中，使用χ 2参数对应于RMSEA为0.05的分布。Lavaan将测试结果报告为拟合统计之一。

那么这对我们有什么帮助呢？非中心参数（λ ）在lavaan的RMSEA测试实际上是χ 2 - d ˚Fχ2-dF对应于RMSEA为0.05的值。

​

因此，对于测试，λ 是：

​

对于中等拟合的测试，λ 是：

​

请注意，lavaan的处理方式可能有所不同。

因此，给定模型的自由度和样本量，我们可以计算出非中心性参数（λ ）。给定λ中，χ2 值和模型的自由度，我们可以计算p值进行测试。

R的语法是：
​

示范

​

运行模型并报告拟合度。仅报告统计信息：

 

lavaan (0.5-23.1097) converged normally after  25 iterations

  Number of observations                           301

  Estimator                                         ML
  Minimum Function Test Statistic               42.291
  Degrees of freedom                                21
  P-value (Chi-square)                           0.004

Root Mean Square Error of Approximation:

  RMSEA                                          0.058
  90 Percent Confidence Interval          0.032  0.083
  P-value RMSEA <= 0.05                          0.276

卡方统计意义显着，该完美拟合检验表明，由于样本的变异性。

默认的卡方检验：

pchisq 

[1] 0.003867178

使用上面的公式计算紧密度测试的非中心参数：.0025乘以模型自由度乘以样本大小-1

 ncp.close  

[1] 15.75

计算紧密拟合的卡方检验：

pchisq 

[1] 0.2740353

紧密契合度测试的p值为.27，接近lavaan报告的值。

如果我们降低标准以进行中等拟合的卡方检验：.0064乘以模型自由度乘以样本大小-1

 ncp.med  

[1] 40.32

pchisq 

[1] 0.9199686

我们在模型中观察模型隐含的协方差矩阵的可能性为92％。非常好。

---

最后，SEM从业者通常报告χ 2-test，但通常希望该测试能够检测到模型规范错误，因此在实践中经常将其忽略。

---

PS：潜在变量建模的另一种方法是PLS路径建模。这是一种基于OLS回归的SEM方法。

---

1. MacCallum, R. C., Browne, M. W., & Sugawara, H. M. (1996). Power analysis and determination of sample size for covariance structure modeling. Psychological Methods, 1(2), 130–149. https://doi.org/10.1037/1082-989X.1.2.130 ↩