原文链接:http://tecdat.cn/?p=9484
目录
介绍
下面以物种多样性为例子展示了如何在R语言中进行相关分析和线性回归分析。
怎么做测试
相关和线性回归示例
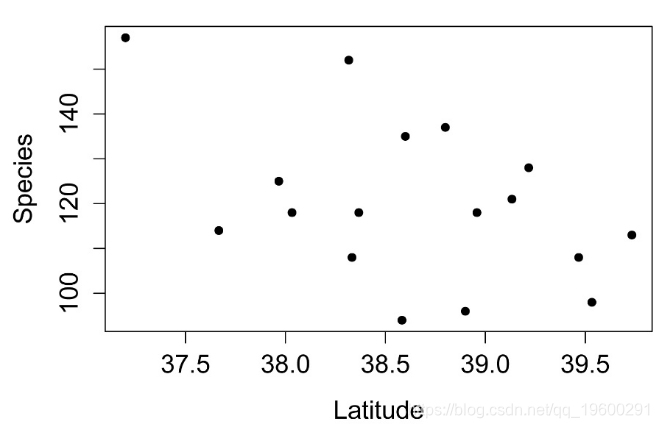
数据简单图
相关性
可以使用 cor.test函数。它可以执行Pearson,Kendall和Spearman相关。
皮尔逊相关
皮尔逊相关是最常见的相关形式。假设数据是线性相关的,并且残差呈正态分布。
肯德尔相关
肯德尔秩相关是一种非参数检验,它不假设数据的分布或数据是线性相关的。它对数据进行排名以确定相关程度。
斯皮尔曼相关
Spearman等级相关性是一种非参数检验,它不假设数据的分布或数据是线性相关的。它对数据进行排序以确定相关程度,并且适合于顺序测量。
线性回归
线性回归可以使用 lm函数执行。可以使用lmrob函数执行稳健回归。
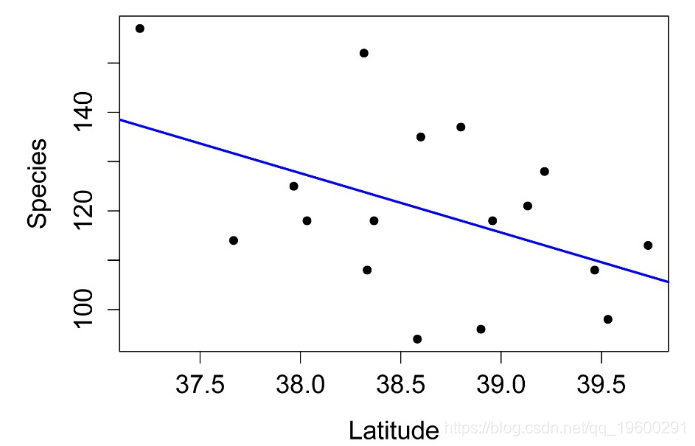
绘制线性回归
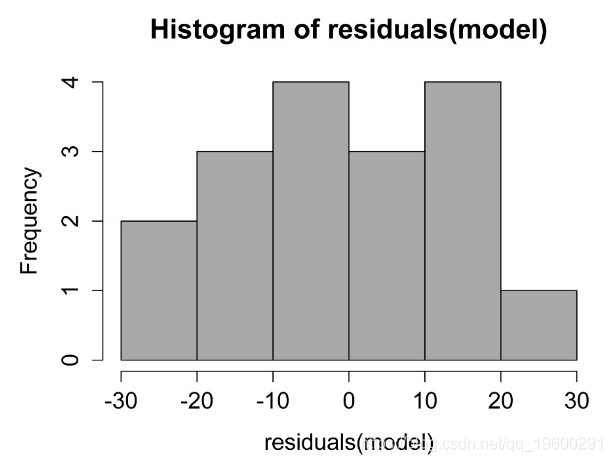
检查模型的假设
线性模型中残差的直方图。这些残差的分布应近似正态。
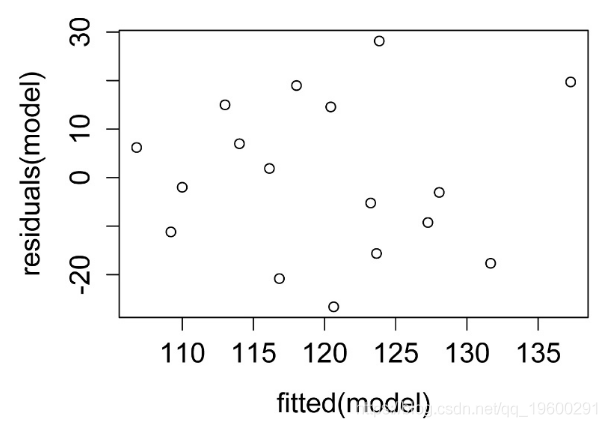
残差与预测值的关系图。残差应无偏且均等。
稳健回归
该线性回归对响应变量中的异常值不敏感。
绘制模型
线性回归示例
功率分析
功率分析的相关性