原文链接:http://tecdat.cn/?p=8417
介绍
如今,几乎我们使用的每个应用程序中都有大量数据-在Spotify上听音乐,在Instagram上浏览朋友的图像,或者在YouTube上观看新的预告片
对于单个用户来说这不是问题。但是,想象一下同时处理成千上万的请求(如果不是上百万)具有大数据的请求。必须以某种方式减少这些数据流,以便我们能够物理上将其提供给用户-这就是数据压缩的开始。
压缩技术很多,它们的用法和兼容性也各不相同。例如,某些压缩技术仅适用于音频文件,例如著名的MPEG-2音频层III(MP3)编解码器。
压缩有两种主要类型:
- 无损:即使我们不太“精打细算”,数据完整性和准确性也是首选
- 有损:数据完整性和准确性并不像我们提供服务的速度那么重要-想象一下实时视频传输,其中“实时”传输比拥有高质量视频更为重要
例如,使用Autoencoders,我们可以分解此图像并将其表示为下面的32矢量代码。使用它,我们可以重建图像。当然,这是有损压缩的一个示例,因为我们已经丢失了很多信息。
不过,我们可以使用完全相同的技术,通过为表示分配更多的空间来更精确地做到这一点:
什么是自动编码器?
根据定义,自动编码器是一种自动对某些内容进行编码的技术。通过使用神经网络,自动编码器能够学习如何将数据(在我们的情况下为图像)分解为相当小的数据位,然后使用该表示形式,将原始数据尽可能地重建为原始数据。
此任务有两个关键组件:
- 编码器:学习如何将原始输入压缩为小的编码
- 解码器:了解如何从编码器生成的编码中恢复原始数据
对这两者进行共生训练,以获得最有效的数据表示形式,我们可以从中重建原始数据,而不会丢失太多数据。
解码器
该解码器的工作原理类似的方式来编码,但周围的其他方式。它学习读取而不是生成这些压缩的代码表示形式,并根据该信息生成图像。显然,其目的是使重建时的损失最小化。
通过使用均方误差(MSE)将重建图像与原始图像进行比较来评估输出-与原始图像越相似,误差就越小。
此时,我们向后传播并更新从解码器到编码器的所有参数。因此,基于输入和输出图像之间的差异,解码器和编码器都将在其工作时进行评估,并更新其参数以变得更好。
建立一个自动编码器
Keras是一个Python框架,可简化神经网络的构建。它允许我们堆叠不同类型的层以创建深度神经网络-我们将构建自动编码器。
首先,让我们使用pip安装Keras:
$ pip install keras
预处理数据
同样,我们将使用LFW数据集。像往常一样,对于此类项目,我们将对数据进行预处理,以使我们的自动编码器更轻松地完成工作。
为此,我们将首先定义几个路径 :
# http://www.cs.columbia.edu/CAVE/databases/pubfig/download/lfw_attributes.txt
ATTRS_NAME = "lfw_attributes.txt"
# http://vis-www.cs.umass.edu/lfw/lfw-deepfunneled.tgz
IMAGES_NAME = "lfw-deepfunneled.tgz"
# http://vis-www.cs.umass.edu/lfw/lfw.tgz
RAW_IMAGES_NAME = "lfw.tgz"
然后,我们将使用两个函数-一个将原始矩阵转换为图像并将颜色系统更改为RGB:
def decode_image_from_raw_bytes(raw_bytes):
img = cv2.imdecode(np.asarray(bytearray(raw_bytes), dtype=np.uint8), 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
return img
另一个是实际加载数据集并使其适应我们的需求:
def load_lfw_dataset(
use_raw=False,
dx=80, dy=80,
dimx=45, dimy=45):
# Read attrs
df_attrs = pd.read_csv(ATTRS_NAME, sep=' ', skiprows=1)
df_attrs = pd.DataFrame(df_attrs.iloc[:, :-1].values, columns=df_attrs.columns[1:])
imgs_with_attrs = set(map(tuple, df_attrs[["person", "imagenum"]].values))
# Read photos
all_photos = []
photo_ids = []
# tqdm in used to show progress bar while reading the data in a notebook here, you can change
# tqdm_notebook to use it outside a notebook
with tarfile.open(RAW_IMAGES_NAME if use_raw else IMAGES_NAME) as f:
for m in tqdm.tqdm_notebook(f.getmembers()):
# Only process image files from the compressed data
if m.isfile() and m.name.endswith(".jpg"):
# Prepare image
img = decode_image_from_raw_bytes(f.extractfile(m).read())
# Crop only faces and resize it
img = img[dy:-dy, dx:-dx]
img = cv2.resize(img, (dimx, dimy))
# Parse person and append it to the collected data
fname = os.path.split(m.name)[-1]
fname_splitted = fname[:-4].replace('_', ' ').split()
person_id = ' '.join(fname_splitted[:-1])
photo_number = int(fname_splitted[-1])
if (person_id, photo_number) in imgs_with_attrs:
all_photos.append(img)
photo_ids.append({'person': person_id, 'imagenum': photo_number})
photo_ids = pd.DataFrame(photo_ids)
all_photos = np.stack(all_photos).astype('uint8')
# Preserve photo_ids order!
all_attrs = photo_ids.merge(df_attrs, on=('person', 'imagenum')).drop(["person", "imagenum"], axis=1)
return all_photos, all_attrs
实施自动编码器
import numpy as np
X, attr = load_lfw_dataset(use_raw=True, dimx=32, dimy=32)
我们的数据X以3D矩阵的形式存在于矩阵中,这是RGB图像的默认表示形式。通过提供三个矩阵-红色,绿色和蓝色,这三个矩阵的组合产生了图像颜色。
这些图像的每个像素将具有较大的值,范围从0到255。通常,在机器学习中,我们倾向于使值较小,并以0为中心,因为这有助于我们的模型更快地训练并获得更好的结果,因此让我们对图像进行归一化:
X = X.astype('float32') / 255.0 - 0.5
现在,如果我们测试X数组的最小值和最大值,它将是-.5和.5,您可以验证:
print(X.max(), X.min())
0.5 -0.5
为了能够看到图像,让我们创建一个show_image函数。0.5由于像素值不能为负,它将添加到图像中:
import matplotlib.pyplot as plt
def show_image(x):
plt.imshow(np.clip(x + 0.5, 0, 1))
现在,让我们快速浏览一下我们的数据:
show_image(X[6])
现在让我们将数据分为训练和测试集:
from sklearn.model_selection import train_test_split
X_train, X_test = train_test_split(X, test_size=0.1, random_state=42)
sklearn train_test_split()函数能够通过给它测试比率来分割数据,其余的当然是训练量。的random_state,你会看到很多机器学习,用来产生相同的结果,不管你有多少次运行代码。
现在该模型了:
from keras.layers import Dense, Flatten, Reshape, Input, InputLayer
from keras.models import Sequential, Model
def build_autoencoder(img_shape, code_size):
# The encoder
encoder = Sequential()
encoder.add(InputLayer(img_shape))
encoder.add(Flatten())
encoder.add(Dense(code_size))
# The decoder
decoder = Sequential()
decoder.add(InputLayer((code_size,)))
decoder.add(Dense(np.prod(img_shape))) # np.prod(img_shape) is the same as 32*32*3, it's more generic than saying 3072
decoder.add(Reshape(img_shape))
return encoder, decoder
此函数将image_shape(图像尺寸)和code_size(输出表示的大小)作为参数。
从逻辑上讲,该值越小code_size,图像将压缩得越多,但是保存的功能就越少,并且所复制的图像与原始图像的差异会更大。
由于网络体系结构不接受3D矩阵,因此该Flatten层的工作是将(32,32,3)矩阵展平为一维数组(3072)。
编码器中的最后一层是该Dense层,这是此处的实际神经网络。它试图找到实现最佳输出的最佳参数-在我们的例子中是编码,我们将其输出大小(也是其中的神经元数量)设置为code_size。
解码器也是顺序模型。它接受输入(编码)并尝试以行的形式重构它。然后,32x32x3通过Dense层将其堆叠成矩阵。最后Reshape一层会将其重塑为图像。
现在,将它们连接在一起并开始我们的模型:
# Same as (32,32,3), we neglect the number of instances from shape
IMG_SHAPE = X.shape[1:]
encoder, decoder = build_autoencoder(IMG_SHAPE, 32)
inp = Input(IMG_SHAPE)
code = encoder(inp)
reconstruction = decoder(code)
autoencoder = Model(inp,reconstruction)
autoencoder.compile(optimizer='adamax', loss='mse')
print(autoencoder.summary())
之后,我们通过Model使用inp和reconstruction参数创建一个链接它们,并使用adamax优化器和mse损失函数对其进行编译。
在这里编译模型意味着定义其目标以及达到目标的方式。在我们的上下文中,目标是最小化,mse并通过使用优化程序来达到此目的-从本质上讲,这是一种经过调整的算法,可以找到全局最小值。
结果:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_6 (InputLayer) (None, 32, 32, 3) 0
_________________________________________________________________
sequential_3 (Sequential) (None, 32) 98336
_________________________________________________________________
sequential_4 (Sequential) (None, 32, 32, 3) 101376
=================================================================
Total params: 199,712
Trainable params: 199,712
Non-trainable params: 0
_________________________________________________________________
在这里我们可以看到输入是32,32,3。
隐藏层是32,这的确是我们选择的编码大小,最后,您看到的解码器输出是(32,32,3)。
模型:
history = autoencoder.fit(x=X_train, y=X_train, epochs=20,
validation_data=[X_test, X_test])
在本例中,我们将比较构造的图像和原始图像,因此x和y都等于X_train。理想情况下,输入等于输出。
该epochs变量定义多少次,我们要训练数据通过模型过去了,validation_data是我们用来评估训练后的模型验证组:
Train on 11828 samples, validate on 1315 samples
Epoch 1/20
11828/11828 [==============================] - 3s 272us/step - loss: 0.0128 - val_loss: 0.0087
Epoch 2/20
11828/11828 [==============================] - 3s 227us/step - loss: 0.0078 - val_loss: 0.0071
.
.
.
Epoch 20/20
11828/11828 [==============================] - 3s 237us/step - loss: 0.0067 - val_loss: 0.0066
我们可以将 损失可视化,以获得 概述。
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
我们可以看到,在第三个时期之后,损失没有明显的进展。
这也可能导致模型过度拟合,从而使其在训练和测试数据集之外的新数据上的表现不佳。
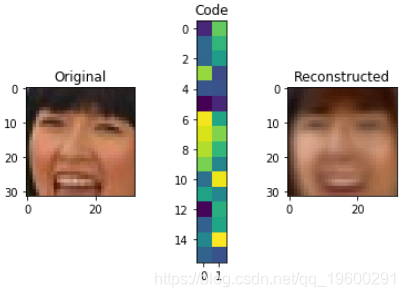
现在,最令人期待的部分-让我们可视化结果:
def visualize(img,encoder,decoder):
"""Draws original, encoded and decoded images"""
# img[None] will have shape of (1, 32, 32, 3) which is the same as the model input
code = encoder.predict(img[None])[0]
reco = decoder.predict(code[None])[0]
plt.subplot(1,3,1)
plt.title("Original")
show_image(img)
plt.subplot(1,3,2)
plt.title("Code")
plt.imshow(code.reshape([code.shape[-1]//2,-1]))
plt.subplot(1,3,3)
plt.title("Reconstructed")
show_image(reco)
plt.show()
for i in range(5):
img = X_test[i]
visualize(img,encoder,decoder)
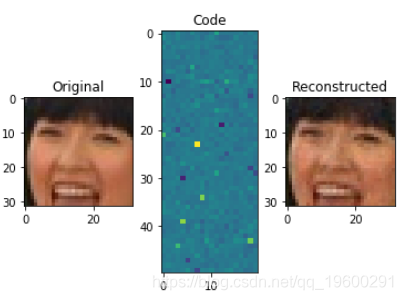
现在,让我们增加code_size至1000:
我们刚刚做的就是主成分分析(PCA),这是一种降维技术。我们可以通过生成较小的新功能来使用它来减小功能集的大小,但是仍然可以捕获重要信息。
主成分分析是自动编码器的一种非常流行的用法。
图像去噪
自动编码器的另一种流行用法是去噪。让我们在图片中添加一些随机噪声:
def apply_gaussian_noise(X, sigma=0.1):
noise = np.random.normal(loc=0.0, scale=sigma, size=X.shape)
return X + noise
在这里,我们从标准正态分布中添加了一些随机噪声,其大小为sigma,默认为0.1。
作为参考,这是具有不同sigma值的噪声的样子:
plt.subplot(1,4,1)
show_image(X_train[0])
plt.subplot(1,4,2)
show_image(apply_gaussian_noise(X_train[:1],sigma=0.01)[0])
plt.subplot(1,4,3)
show_image(apply_gaussian_noise(X_train[:1],sigma=0.1)[0])
plt.subplot(1,4,4)
show_image(apply_gaussian_noise(X_train[:1],sigma=0.5)[0])
正如我们所看到的,几乎看不到图像的sigma增加0.5。我们将尝试从σ为的嘈杂图像中再生原始图像0.1。
我们将为此生成的模型与之前的模型相同,尽管我们将进行不同的训练。这次,我们将使用原始和相应的噪点图像对其进行训练:
code_size = 100
# We can use bigger code size for better quality
encoder, decoder = build_autoencoder(IMG_SHAPE, code_size=code_size)
inp = Input(IMG_SHAPE)
code = encoder(inp)
reconstruction = decoder(code)
autoencoder = Model(inp, reconstruction)
autoencoder.compile('adamax', 'mse')
for i in range(25):
print("Epoch %i/25, Generating corrupted samples..."%(i+1))
X_train_noise = apply_gaussian_noise(X_train)
X_test_noise = apply_gaussian_noise(X_test)
# We continue to train our model with new noise-augmented data
autoencoder.fit(x=X_train_noise, y=X_train, epochs=1,
validation_data=[X_test_noise, X_test])
现在让我们看一下模型结果:
X_test_noise = apply_gaussian_noise(X_test)
for i in range(5):
img = X_test_noise[i]
visualize(img,encoder,decoder)
结论
自动编码器可用于主成分分析,这是一种降维技术,图像去噪等。