介绍
大多数时候,我能够破解特征工程部分,但可能没有使用多个模型的集合。
在本文中,我将向您介绍集成建模的基础知识。 另外,为了向您提供有关集合建模的实践经验,我们将使用R对hackathon问题进行集成。
1.什么是集成?
通常,集成是一种组合两种或多种类似或不同类型算法的技术,称为基础学习者。这样做是为了建立一个更加健壮的系统,其中包含了所有基础学习者的预测。可以理解为多个交易者之间的会议室会议,以决定股票的价格是否会上涨。
由于他们都对股票市场有不同的理解,因此从问题陈述到期望的结果有不同的映射功能。因此,他们应该根据自己对市场的理解对股票价格做出各种预测。
2.集合的类型
在进一步详细介绍之前,您应该了解的一些基本概念是:
- 平均:它被定义为 在回归问题的情况下或在预测分类问题的概率时从模型中获取预测的平均值。
- 多数投票:它被 定义为 在预测分类问题的结果的同时,从多个模型预测中以最大投票/推荐进行预测。
- 加权平均值:在此,不同的权重应用于来自多个模型的预测,然后取平均值 。
这些是一些主要使用的技术:
- Bagging: Bagging也称为bootstrap聚合。
增强的一些例子是XGBoost,GBM,ADABOOST等。
- 堆叠:在堆叠多层机器时,学习模型彼此叠加,每个模型将其预测传递给上面层中的模型,顶层模型根据模型下面的模型输出做出决策。
3.集合的优点和缺点
3.1优点
- 集成是一种经过验证的方法,可以提高模型的准确性,适用于大多数情况。
- 集成使模型更加稳健和稳定,从而确保在大多数情况下测试用例具有良好的性能。
- 您可以使用集成来捕获数据中的线性和简单以及非线性复杂关系。这可以通过使用两个不同的模型并形成两个集合来完成。
3.2缺点
- 集成减少了模型的可解释性,并且很难在最后绘制任何关键的业务见解。
- 这非常耗时,因此可能不是实时应用程序的最佳选择。
4.在R中实施集合的实用指南
#让我们看一下数据集数据的结构
'data.frame':614 obs。13个变量:
$ ApplicantIncome:int 5849 4583 3000 2583 6000 5417 2333 3036 4006 12841 ...
$ CoapplicantIncome:num 0 1508 0 2358 0 ...
$ LoanAmount:int NA 128 66 120 141 267 95 158 168 349 ...
$ Loan_Amount_Term:int 360 360 360 360 360 360 360 360 360 360 ...
$ Credit_History:int 1 1 1 1 1 1 1 0 1 1 ...
#使用中位数输入缺失值
preProcValues < - preProcess(data,method = c(“medianImpute”,“center”,“scale”))
#Spliting训练根据结果分为两部分:75%和25%
index < - createDataPartition(data_processed $ Loan_Status,p = 0.75,list = FALSE)
trainSet < - data_processed [index,]
testSet < - data_processed [-index,]我将数据分成两部分,我将用它来模拟训练和测试操作。我们现在定义训练控件以及预测变量和结果变量:
#定义多个模型的训练控件
fitControl < - trainControl(
method =“cv”, savePredictions ='final',
classProbs = T)
#Defining预测器和结果现在让我们开始训练随机森林并在我们创建的测试集上测试其准确性:
#检查随机森林模型的准确性
混淆矩阵和统计
参考
预测N Y.
N 28 20
Y 9 96
准确度:0.8105
95%CI:(0.7393,0.8692)
无信息率:0.7582
P值[Acc> NIR]:0.07566
Kappa:0.5306
Mcnemar的测试P值:0.06332
灵敏度:0.7568
特异性:0.8276
Pos Pred价值:0.5833
Neg Pred值:0.9143
患病率:0.2418
检测率:0.1830
检测流行率:0.3137
平衡准确度:0.7922
'正面'类:N我们使用随机森林模型获得了0.81的准确度。让我们看看KNN的表现:
#训练knn模型
#Predicting使用knn模型
testSet $ pred_knn <-predict(object = model_knn,testSet [,predictors])
#检查随机森林模型的准确性
混淆矩阵和统计
参考
预测N Y.
N 29 19
是2 103
准确度:0.8627
95%CI:(0.7979,0.913)
无信息率:0.7974
P值[Acc> NIR]:0.0241694
Kappa:0.6473
Mcnemar的测试P值:0.0004803
灵敏度:0.9355
特异性:0.8443
Pos Pred价值:0.6042
Neg Pred值:0.9810
患病率:0.2026
检测率:0.1895
检测流行率:0.3137
平衡准确度:0.8899
'正面'类:N我们能够通过单独的KNN模型获得0.86的准确度。在我们继续创建这三者的集合之前,让我们看看Logistic回归的表现。
#Training Logistic回归模型
#Predicting使用knn模型
testSet $ pred_lr <-predict(object = model_lr,testSet [,predictors])
#检查随机森林模型的准确性
混淆矩阵和统计
参考
预测N Y.
N 29 19
是2 103
准确度:0.8627
95%CI:(0.7979,0.913)
无信息率:0.7974
P值[Acc> NIR]:0.0241694
Kappa:0.6473
Mcnemar的测试P值:0.0004803
灵敏度:0.9355
特异性:0.8443
Pos Pred价值:0.6042
Neg Pred值:0.9810
患病率:0.2026
检测率:0.1895
检测流行率:0.3137
平衡准确度:0.8899
'正面'类:N逻辑回归也给出了0.86的准确度。
现在,让我们尝试用这些模型形成集合的不同方法,如我们所讨论的:
- 平均:在此,我们将平均三个模型的预测。由于预测是“Y”或“N”,因此平均值对于此二进制分类没有多大意义。但是,我们可以对观察概率的平均值进行平均处理。
#Predicting概率
testSet $ pred_rf_prob <-predict(object = model_rf,testSet [,predictors],type ='prob')
testSet $ pred_knn_prob <-predict(object = model_knn,testSet [,predictors],type ='prob')
testSet $ pred_lr_prob <-predict(object = model_lr,testSet [,predictors],type ='prob')
#Spits到0.5的二进制类 多数表决:在多数表决中,我们将为大多数模型预测的观察指定预测。由于我们有三个模型用于二进制分类任务,因此无法实现平局。#多数投票 加权平均值:我们可以采用加权平均值,而不是采用简单平均值。通常,对于更准确的模型,预测的权重很高。让我们将0.5分配给logistic回归,将0.25分配给KNN和随机森林。#Taking加权平均预测
#Spits到0.5的二进制类 在继续讨论之前,我想回顾一下我们之前讨论过的关于个体模型精度和模型间预测相关性的两个重要标准,这些标准必须得到满足。在上面的集合中,我已经跳过检查三个模型的预测之间的相关性。我随机选择了这三个模型来演示这些概念。如果预测高度相关,那么使用这三个预测可能不会比单个模型提供更好的结果。但你明白了。对?到目前为止,我们在顶层使用了简单的公式。相反,我们可以使用另一种机器学习模型,这实际上就是堆叠。我们可以使用线性回归来制作线性公式,用于在回归问题中进行预测,以便在分类问题的情况下将底层模型预测映射到结果或逻辑回归。
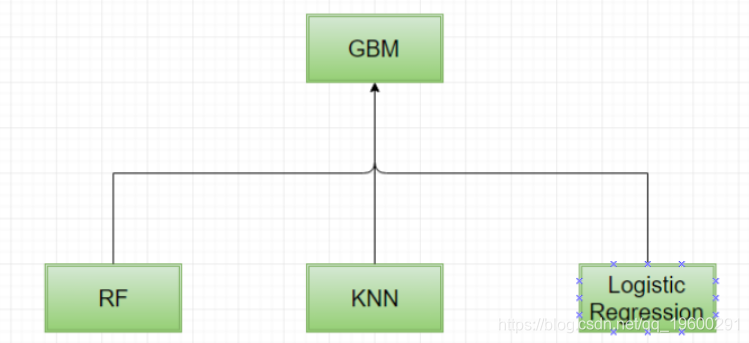
在同一个例子中,让我们尝试将逻辑回归和GBM应用为顶层模型。请记住,我们将采取以下步骤:
- 在训练数据上训练各个基础层模型。
- 预测使用每个基础层模型来训练数据和测试数据。
- 现在,再次对顶层模型进行训练,对底层模型进行训练数据的预测。
- 最后,使用顶层模型预测底层模型的预测,这些模型是为测试数据而做出的。
在步骤2中需要注意的一件非常重要的事情是,您应始终对训练数据进行包预测,否则基础层模型的重要性将仅取决于基础层模型可以如何调用训练数据。
-
步骤1:在训练数据上训练各个基础层模型
#Defining 控制
fitControl < - trainControl(
method =“cv”, savePredictions ='final',#保存最佳参数组合的折叠预测
classProbs = T#保存折叠预测的类概率
)
#Defining预测器和结果
#Training随机森林模型
#训练knn模型
#Training逻辑回归模型 -
步骤2:使用每个基础层模型预测训练数据和测试数据
#Predicting训练数据的折叠预测概率
#Predicting测试数据的概率-
步骤3:现在再次训练顶层模型对底层模型的预测已经对训练数据进行了预测
首先,让我们从GBM模型开始作为顶层模型。
#Predictors用于顶层模型
predictors_top <-c( 'OOF_pred_rf', 'OOF_pred_knn', 'OOF_pred_lr')
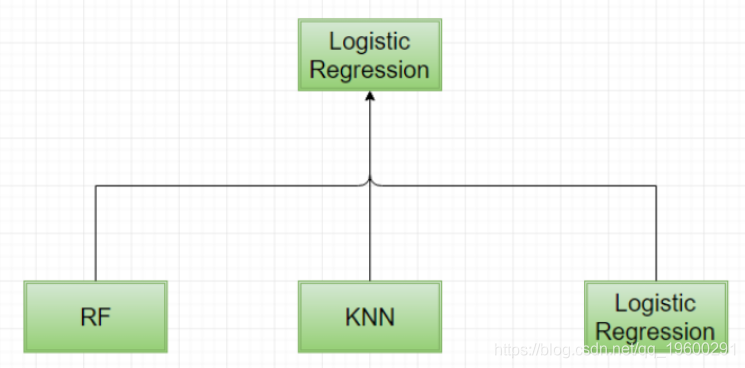
#GBM作为顶层模型 同样,我们也可以使用逻辑回归创建一个集合作为顶层模型。
#Logistic回归作为顶层模型
model_glm < -
( [,predictors_top], trControl = fitControl,tuneLength = 3)-
步骤4:最后,使用顶层模型预测已经为测试数据而做出的底层模型的预测
#predict使用GBM顶层模型
测试集$ gbm_stacked <-predict(model_gbm,测试集[,predictors_top])
#predict使用logictic回归顶层模型
测试集$ glm_stacked <-predict(model_glm,测试集[,predictors_top])请注意, 选择模型非常重要,以便从整体中获得最佳效果。我们讨论的 拇指规则将极大地帮助你。