原文链接:http://tecdat.cn/?p=6632
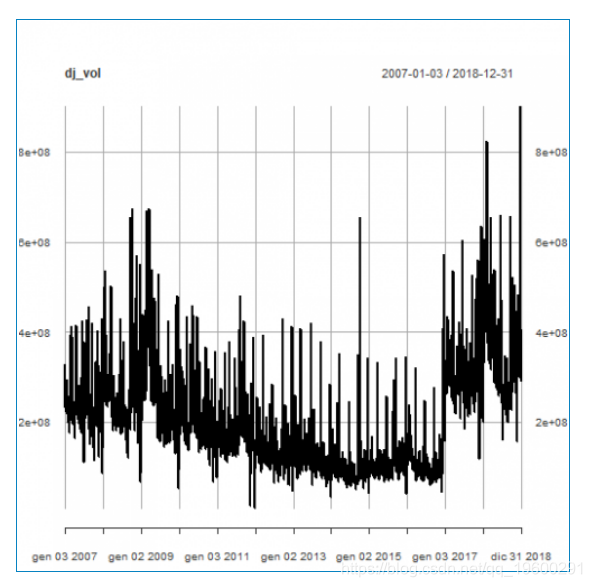
我将建立道琼斯工业平均指数(DJIA)日交易量对数比的ARMA-GARCH模型。
获取数据
load(file='DowEnvironment.RData')
日交易量
每日交易量内发生的 变化。
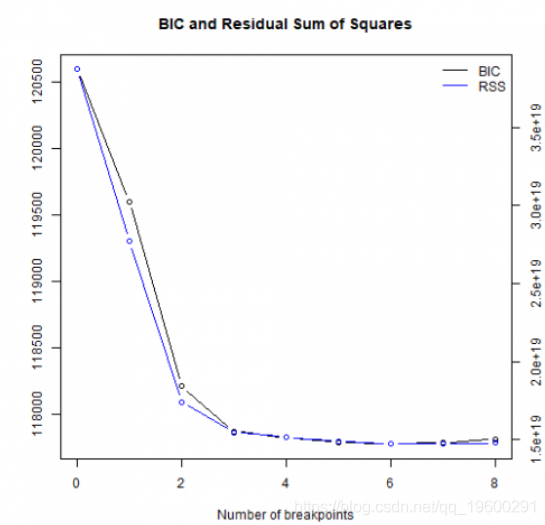
首先,我们验证具有常数均值的线性回归在统计上是显着的。
在休息时间= 6时达到最小BIC。
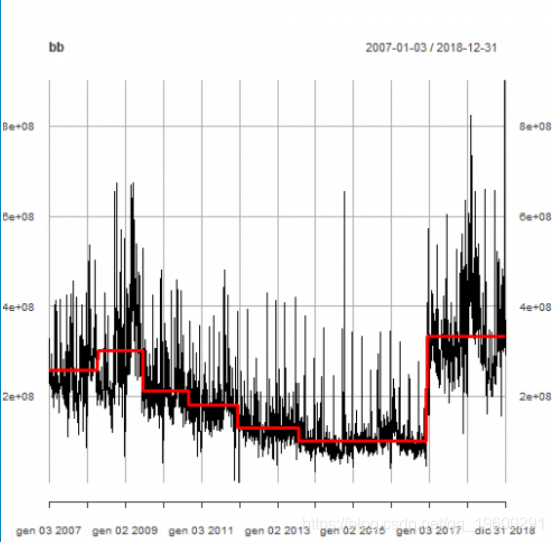
以下是道琼斯日均交易量与水平变化(红线) 。
lwd = c(3,1), col = c("red", "black"))
每日交易量对数比率模型
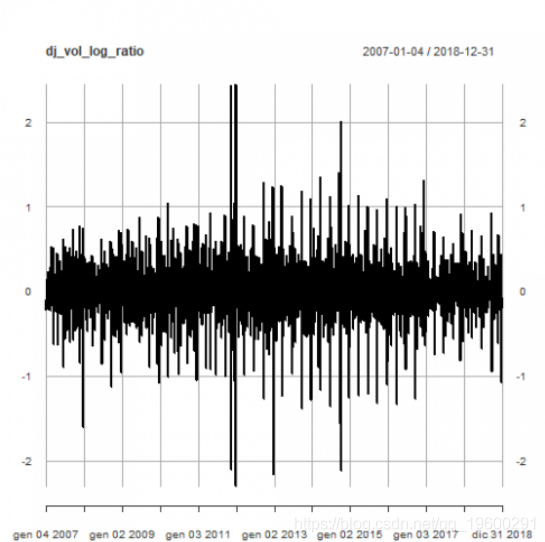
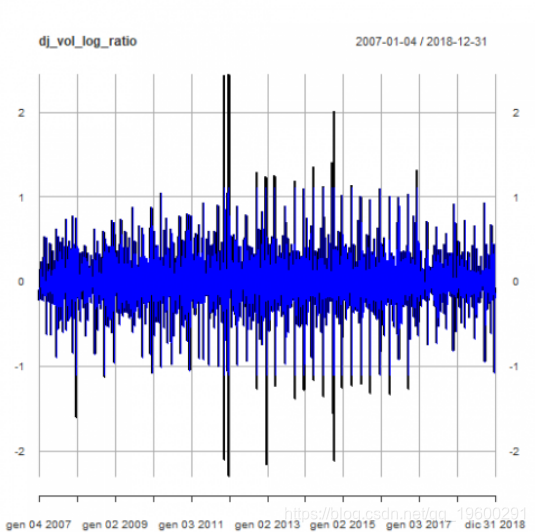
每日交易量对数比率:
plot(dj_vol_log_ratio)
异常值检测
下面我们将原始时间序列与调整后的异常值进行比较。
相关图
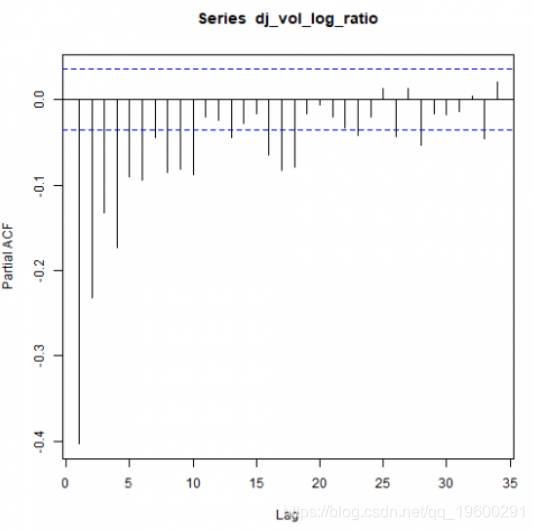
pacf(dj_vol_log_ratio)
上图可能表明 ARMA(p,q)模型的p和q> 0.
单位根测试
我们 提供Augmented Dickey-Fuller测试。
根据 测试统计数据与临界值进行比较,我们拒绝单位根存在的零假设。
ARMA模型
我们现在确定时间序列的ARMA结构,以便对结果残差运行ARCH效果测试。
ma1系数在统计上不显着。因此,我们尝试使用以下ARMA(2,3)模型。
所有系数都具有统计显着性,AIC低于第一个模型。然后我们尝试使用ARMA(1,2)。
该模型在集合中具有最高的AIC,并且所有系数具有统计显着性。
我们还可以尝试 进一步验证。
以“O”为顶点的左上角三角形似乎位于{(1,2),(2,2),(1,3),(2,3)}之内,代表潜在的集合( p,q)根据eacf()函数输出的值。
我们已经在集合{(3,2)(2,3)(1,2)}内验证了具有(p,q)阶的ARMA模型。让我们试试{(2,2)(1,3)}
ar2系数在统计上不显着。
ma3系数在统计上不显着。
ARCH效果测试
如果ARCH效应对于我们的时间序列的残差具有统计显着性,则需要GARCH模型。
我们测试候选平均模型ARMA(2,3)。
根据报告的p值,我们拒绝无ARCH效应的零假设。
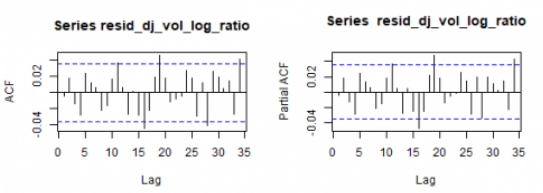
让我们看一下残差相关图。
par(mfrow=c(1,2))
acf(resid_dj_vol_log_ratio)
pacf(resid_dj_vol_log_ratio)
我们测试了第二个候选平均模型ARMA(1,2)。
根据报告的p值,我们拒绝无ARCH效应的零假设。
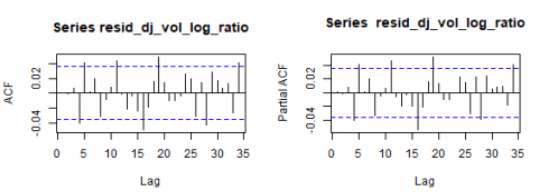
让我们看一下残差相关图。
par(mfrow=c(1,2))
acf(resid_dj_vol_log_ratio)
pacf(resid_dj_vol_log_ratio)
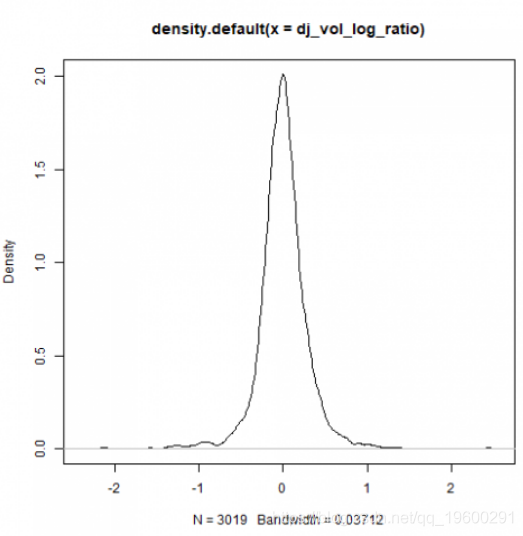
要检查 对数比率内的不对称性,将显示汇总统计数据和密度图。
plot(density(dj_vol_log_ratio))
因此,对于每日交易量对数比,还将提出eGARCH模型。
为了将结果与两个候选平均模型ARMA(1,2)和ARMA(2,3)进行比较,我们进行了两次拟合
ARMA-GARCH:ARMA(1,2)+ eGARCH(1,1)
所有系数都具有统计显着性。然而,基于上面报道的标准化残差p值的加权Ljung-Box检验,我们拒绝了对于本模型没有残差相关性的零假设。
ARMA-GARCH:ARMA(2,3)+ eGARCH(1,1)
所有系数都具有统计显着性。没有找到标准化残差或标准化平方残差的相关性。模型可以正确捕获所有ARCH效果。调整后的Pearson拟合优度检验不拒绝零假设,即标准化残差的经验分布和所选择的理论分布是相同的。然而:
*对于其中一些模型参数随时间变化恒定的Nyblom稳定性测试零假设被拒绝
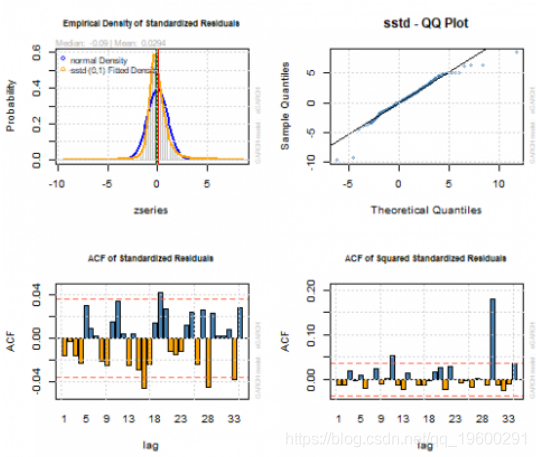
par(mfrow=c(2,2))
plot(garchfit, which=8)
plot(garchfit, which=9)
plot(garchfit, which=10)
plot(garchfit, which=11)我们用平均模型拟合(红线)和条件波动率(蓝线)显示原始道琼斯日均交易量对数时间序列。
对数波动率分析
以下是我们的模型ARMA(2,2)+ eGARCH(1,1)产生的条件波动率图。
plot(cond_volatility)
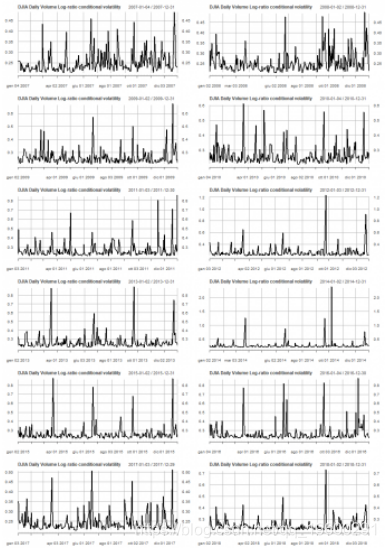
显示了按年度的条件波动率的线图。par(mfrow=c(6,2))
pl <- lapply(2007:2018, function(x) { plot(cond_volatility[as.character(x)], main = "DJIA Daily Volume Log-ratio conditional volatility")})
pl
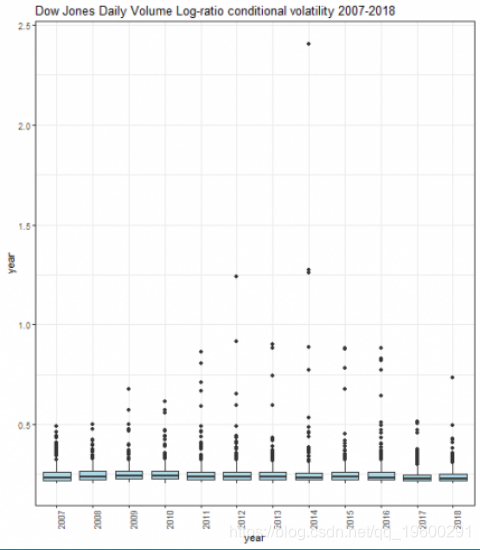
显示了按年度计算的条件波动率框图。
结论
我们研究了基本统计指标,如平均值,偏差,偏度和峰度,以了解多年来价值观的差异,以及价值分布对称性和尾部。从这些摘要开始,我们获得了平均值,中位数,偏度和峰度指标的有序列表,以更好地突出多年来的差异。
密度图可以了解我们的经验样本分布的不对称性和尾部性。
对于对数回报,我们构建了ARMA-GARCH模型(指数GARCH,特别是作为方差模型),以获得条件波动率。同样,可视化作为线和框图突出显示了年内和年之间的条件波动率变化。这种调查的动机是,波动率是变化幅度的指标,用简单的词汇表示,并且是应用于资产的对数收益时的基本风险度量。有几种类型的波动性(有条件的,隐含的,实现的波动率)。
交易量可以被解释为衡量市场活动幅度和投资者兴趣的指标。计算交易量指标(包括波动率)可以了解这种活动/利息水平如何随时间变化。