Fox Ciel is participating in a party in Prime Kingdom. There are n foxes there (include Fox Ciel). The i-th fox is ai years old.
They will have dinner around some round tables. You want to distribute foxes such that:
- Each fox is sitting at some table.
- Each table has at least 3 foxes sitting around it.
- The sum of ages of any two adjacent foxes around each table should be a prime number.
If k foxes f1, f2, ..., fk are sitting around table in clockwise order, then for 1 ≤ i ≤ k - 1: fi and fi + 1 are adjacent, and f1 and fk are also adjacent.
If it is possible to distribute the foxes in the desired manner, find out a way to do that.
The first line contains single integer n (3 ≤ n ≤ 200): the number of foxes in this party.
The second line contains n integers ai (2 ≤ ai ≤ 104).
If it is impossible to do this, output "Impossible".
Otherwise, in the first line output an integer m (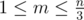
): the number of tables.
Then output m lines, each line should start with an integer k -=– the number of foxes around that table, and then k numbers — indices of fox sitting around that table in clockwise order.
If there are several possible arrangements, output any of them.
4
3 4 8 9
1
4 1 2 4 3
5
2 2 2 2 2
Impossible
12
2 3 4 5 6 7 8 9 10 11 12 13
1
12 1 2 3 6 5 12 9 8 7 10 11 4
24
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
3
6 1 2 3 6 5 4
10 7 8 9 12 15 14 13 16 11 10
8 17 18 23 22 19 20 21 24
In example 1, they can sit around one table, their ages are: 3-8-9-4, adjacent sums are: 11, 17, 13 and 7, all those integers are primes.
In example 2, it is not possible: the sum of 2+2 = 4 is not a prime number.
题意：
给出n个人， 以及每个人的值， 要求他们坐在一些桌子上面， 每个桌子如果有人坐， 就必须做3个人以上。 并且相邻的两个人的值加起来必须是素数。每个人的值都>=2.如果可能输出桌子数目ans，接下来ans行首先输出每个桌子的人数，然后顺时针输出每个人的编号。
题解：
由大于等于2这个条件， 可以知道素数都是奇数， 那么很明显就需要一奇一偶相邻这样做， 那么一个桌子上必定有偶数个人。 一个奇数旁边有两个偶数， 一个偶数旁边有两个奇数。
所以可以先判断n是否为偶数， 如果是奇数直接输出不可能。
然后开始奇偶建边， 源点和奇数建边， 权值为2， 因为一个奇数需要和两个偶数匹配； 偶数和汇点建边， 同理权值也为2。
然后， 如果一个奇数和一个偶数相加得到的数是素数， 那么奇数向偶数连一条边， 权值为1。
这样跑一遍网络流， 看结果是否等于n， 如果不相等， 说明不可能。如果可能， dfs一下就可以求出几个桌子， 每个桌子上面几个人了。（在这里我是重新建立了一个无向图，向这个图中加入每条满流边的两个顶点）。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<vector> #include<queue> #include<stack> using namespace std; #define rep(i,a,n) for (int i=a;i<n;i++) #define per(i,a,n) for (int i=n-1;i>=a;i--) #define pb push_back #define fi first #define se second typedef vector<int> VI; typedef long long ll; typedef pair<int,int> PII; const int inf=0x3fffffff; const int maxn=210;//点数的最大值 const int maxm=20500;//边数的最大值 struct Node { int from,to,next; int cap; }edge[maxm]; int tol; int dep[maxn];//dep为点的层次 int head[maxn]; void init() { tol=0; memset(head,-1,sizeof(head)); } void addedge(int u,int v,int w)//第一条边下标必须为偶数 { edge[tol].from=u; edge[tol].to=v; edge[tol].cap=w; edge[tol].next=head[u]; head[u]=tol++; edge[tol].from=v; edge[tol].to=u; edge[tol].cap=0; edge[tol].next=head[v]; head[v]=tol++; } int BFS(int start,int end) { int que[maxn]; int front,rear; front=rear=0; memset(dep,-1,sizeof(dep)); que[rear++]=start; dep[start]=0; while(front!=rear) { int u=que[front++]; if(front==maxn)front=0; for(int i=head[u];i!=-1;i=edge[i].next) { int v=edge[i].to; if(edge[i].cap>0&&dep[v]==-1) { dep[v]=dep[u]+1; que[rear++]=v; if(rear>=maxn)rear=0; if(v==end)return 1; } } } return 0; } int dinic(int start,int end) { int res=0; int top; int stack[maxn];//stack为栈，存储当前增广路 int cur[maxn];//存储当前点的后继 while(BFS(start,end)) { memcpy(cur,head,sizeof(head)); int u=start; top=0; while(1) { if(u==end) { int min=inf; int loc; for(int i=0;i<top;i++) if(min>edge[stack[i]].cap) { min=edge[stack[i]].cap; loc=i; } for(int i=0;i<top;i++) { edge[stack[i]].cap-=min; edge[stack[i]^1].cap+=min; } res+=min; top=loc; u=edge[stack[top]].from; } for(int i=cur[u];i!=-1;cur[u]=i=edge[i].next) if(edge[i].cap!=0&&dep[u]+1==dep[edge[i].to]) break; if(cur[u]!=-1) { stack[top++]=cur[u]; u=edge[cur[u]].to; } else { if(top==0)break; dep[u]=-1; u=edge[stack[--top]].from; } } } return res; } const int N=2e4+100; int prime[N]; bool is[N]; void getPrim() { for(int i=2;i<N;i++) { if(!prime[i]) { prime[++prime[0]] = i; } for(int j=1;(j<=prime[0])&&(i*prime[j]<N);j++) { prime[prime[j]*i] = 1; if(i%prime[j]==0) break; } } } void get() { getPrim(); memset(is,false,sizeof(is)); for(int i=1;i<=prime[0];i++) is[prime[i]]=true; } int vis[maxn]; VI V[maxn]; int a[maxn]; int ans; int st,en; int head1[maxn]; struct edge { int to,next; }e[maxm]; // int tol1=0; void add(int u,int v) { e[++tol1].to=v,e[tol1].next=head1[u],head1[u]=tol1; } void dfs1(int u) { V[ans].pb(u); vis[u]=1; for(int i=head1[u];i;i=e[i].next) { int v=e[i].to; if(vis[v]) continue; dfs1(v); } } int main() { init(); get(); int n; scanf("%d",&n); st=0,en=n+1; rep(i,1,n+1) { scanf("%d",&a[i]); if(a[i]&1) addedge(st,i,2); else addedge(i,en,2); } if(n&1) { return 0*puts("Impossible"); } rep(i,1,n+1) { rep(j,i+1,n+1) { if((a[i]&1)&&(a[j]%2==0)) { if(is[a[i]+a[j]]) addedge(i,j,1); } if((a[i]%2==0)&&(a[j]&1)) { if(is[a[i]+a[j]]) addedge(j,i,1); } } } if(dinic(st,en)==n) { ans=0; memset(vis,0,sizeof(vis)); for(int i=1;i<tol;i+=2) { if(edge[i].cap==1) { add(edge[i].to,edge[i].from),add(edge[i].from,edge[i].to); } } memset(vis,0,sizeof(vis)); rep(i,1,n+1) { if(!vis[i]) ans++,dfs1(i); } printf("%d ",ans); rep(i,1,ans+1) { printf("%d",V[i].size()); rep(j,0,V[i].size()) printf(" %d",V[i][j]); puts(""); } } else puts("Impossible"); return 0; }