1.逻辑回归是怎么防止过拟合的?为什么正则化可以防止过拟合?(大家用自己的话介绍下)
通过正则化来防止过拟合。
通过正则化把许多隐藏的单元权重的影响消除掉,这样这个神经网络就会变成一个小网络,没有那么复杂,这样就可以防止过拟合了。
2.用logiftic回归来进行实践操作,数据不限。
import pandas as pd from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.metrics import classification_report from sklearn.linear_model import LogisticRegression def logistic(): data=pd.read_csv('C:\Users\Administrator\PycharmProjects\python机器学习\data\LogisticRegression.csv') x = data.iloc[:,:3] y = data.iloc[:,3] x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3) std = StandardScaler() x_train=std.fit_transform(x_train) x_test=std.transform(x_test) lg=LogisticRegression() lg.fit(x_train,y_train) print(lg.coef_) lg_pre=lg.predict(x_test) print('准确率:',lg.score(x_test,y_test)) print('召回率:',classification_report(y_test,lg_pre)) if __name__=='__main__': logistic();
结果:
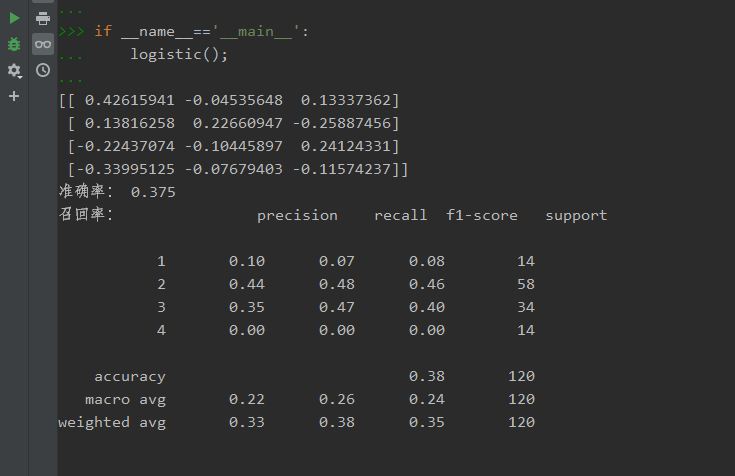
数据集:
admit,gre,gpa,rank
0,380,3.61,3
1,660,3.67,3
1,800,4.0,1
1,640,3.19,4
0,520,2.93,4
1,760,3.0,2
1,560,2.98,1
0,400,3.08,2
1,540,3.39,3
0,700,3.92,2
0,800,4.0,4
0,440,3.22,1
1,760,4.0,1
0,700,3.08,2
1,700,4.0,1
0,480,3.44,3
0,780,3.87,4
0,360,2.56,3
0,800,3.75,2
1,540,3.81,1
0,500,3.17,3
1,660,3.63,2
0,600,2.82,4
0,680,3.19,4
1,760,3.35,2
1,800,3.66,1
1,620,3.61,1
1,520,3.74,4
1,780,3.22,2
0,520,3.29,1
0,540,3.78,4
0,760,3.35,3
0,600,3.4,3
1,800,4.0,3
0,360,3.14,1
0,400,3.05,2
0,580,3.25,1
0,520,2.9,3
1,500,3.13,2
1,520,2.68,3
0,560,2.42,2
1,580,3.32,2
1,600,3.15,2
0,500,3.31,3
0,700,2.94,2
1,460,3.45,3
1,580,3.46,2
0,500,2.97,4
0,440,2.48,4
0,400,3.35,3
0,640,3.86,3
0,440,3.13,4
0,740,3.37,4
1,680,3.27,2
0,660,3.34,3
1,740,4.0,3
0,560,3.19,3
0,380,2.94,3
0,400,3.65,2
0,600,2.82,4
1,620,3.18,2
0,560,3.32,4
0,640,3.67,3
1,680,3.85,3
0,580,4.0,3
0,600,3.59,2
0,740,3.62,4
0,620,3.3,1
0,580,3.69,1
0,800,3.73,1
0,640,4.0,3
0,300,2.92,4
0,480,3.39,4
0,580,4.0,2
0,720,3.45,4
0,720,4.0,3
0,560,3.36,3
1,800,4.0,3
0,540,3.12,1
1,620,4.0,1
0,700,2.9,4
0,620,3.07,2
0,500,2.71,2
0,380,2.91,4
1,500,3.6,3
0,520,2.98,2
0,600,3.32,2
0,600,3.48,2
0,700,3.28,1
1,660,4.0,2
0,700,3.83,2
1,720,3.64,1
0,800,3.9,2
0,580,2.93,2
1,660,3.44,2
0,660,3.33,2
0,640,3.52,4
0,480,3.57,2
0,700,2.88,2
0,400,3.31,3
0,340,3.15,3
0,580,3.57,3
0,380,3.33,4
0,540,3.94,3
1,660,3.95,2
1,740,2.97,2
1,700,3.56,1
0,480,3.13,2
0,400,2.93,3
0,480,3.45,2
0,680,3.08,4
0,420,3.41,4
0,360,3.0,3
0,600,3.22,1
0,720,3.84,3
0,620,3.99,3
1,440,3.45,2
0,700,3.72,2
1,800,3.7,1
0,340,2.92,3
1,520,3.74,2
1,480,2.67,2
0,520,2.85,3
0,500,2.98,3
0,720,3.88,3
0,540,3.38,4
1,600,3.54,1
0,740,3.74,4
0,540,3.19,2
0,460,3.15,4
1,620,3.17,2
0,640,2.79,2
0,580,3.4,2
0,500,3.08,3
0,560,2.95,2
0,500,3.57,3
0,560,3.33,4
0,700,4.0,3
0,620,3.4,2
1,600,3.58,1
0,640,3.93,2
1,700,3.52,4
0,620,3.94,4
0,580,3.4,3
0,580,3.4,4
0,380,3.43,3
0,480,3.4,2
0,560,2.71,3
1,480,2.91,1
0,740,3.31,1
1,800,3.74,1
0,400,3.38,2
1,640,3.94,2
0,580,3.46,3
0,620,3.69,3
1,580,2.86,4
0,560,2.52,2
1,480,3.58,1
0,660,3.49,2
0,700,3.82,3
0,600,3.13,2
0,640,3.5,2
1,700,3.56,2
0,520,2.73,2
0,580,3.3,2
0,700,4.0,1
0,440,3.24,4
0,720,3.77,3
0,500,4.0,3
0,600,3.62,3
0,400,3.51,3
0,540,2.81,3
0,680,3.48,3
1,800,3.43,2
0,500,3.53,4
1,620,3.37,2
0,520,2.62,2
1,620,3.23,3
0,620,3.33,3
0,300,3.01,3
0,620,3.78,3
0,500,3.88,4
0,700,4.0,2
1,540,3.84,2
0,500,2.79,4
0,800,3.6,2
0,560,3.61,3
0,580,2.88,2
0,560,3.07,2
0,500,3.35,2
1,640,2.94,2
0,800,3.54,3
0,640,3.76,3
0,380,3.59,4
1,600,3.47,2
0,560,3.59,2
0,660,3.07,3
1,400,3.23,4
0,600,3.63,3
0,580,3.77,4
0,800,3.31,3
1,580,3.2,2
1,700,4.0,1
0,420,3.92,4
1,600,3.89,1
1,780,3.8,3
0,740,3.54,1
1,640,3.63,1
0,540,3.16,3
0,580,3.5,2
0,740,3.34,4
0,580,3.02,2
0,460,2.87,2
0,640,3.38,3
1,600,3.56,2
1,660,2.91,3
0,340,2.9,1
1,460,3.64,1
0,460,2.98,1
1,560,3.59,2
0,540,3.28,3
0,680,3.99,3
1,480,3.02,1
0,800,3.47,3
0,800,2.9,2
1,720,3.5,3
0,620,3.58,2
0,540,3.02,4
0,480,3.43,2
1,720,3.42,2
0,580,3.29,4
0,600,3.28,3
0,380,3.38,2
0,420,2.67,3
1,800,3.53,1
0,620,3.05,2
1,660,3.49,2
0,480,4.0,2
0,500,2.86,4
0,700,3.45,3
0,440,2.76,2
1,520,3.81,1
1,680,2.96,3
0,620,3.22,2
0,540,3.04,1
0,800,3.91,3
0,680,3.34,2
0,440,3.17,2
0,680,3.64,3
0,640,3.73,3
0,660,3.31,4
0,620,3.21,4
1,520,4.0,2
1,540,3.55,4
1,740,3.52,4
0,640,3.35,3
1,520,3.3,2
1,620,3.95,3
0,520,3.51,2
0,640,3.81,2
0,680,3.11,2
0,440,3.15,2
1,520,3.19,3
1,620,3.95,3
1,520,3.9,3
0,380,3.34,3
0,560,3.24,4
1,600,3.64,3
1,680,3.46,2
0,500,2.81,3
1,640,3.95,2
0,540,3.33,3
1,680,3.67,2
0,660,3.32,1
0,520,3.12,2
1,600,2.98,2
0,460,3.77,3
1,580,3.58,1
1,680,3.0,4
1,660,3.14,2
0,660,3.94,2
0,360,3.27,3
0,660,3.45,4
0,520,3.1,4
1,440,3.39,2
0,600,3.31,4
1,800,3.22,1
1,660,3.7,4
0,800,3.15,4
0,420,2.26,4
1,620,3.45,2
0,800,2.78,2
0,680,3.7,2
0,800,3.97,1
0,480,2.55,1
0,520,3.25,3
0,560,3.16,1
0,460,3.07,2
0,540,3.5,2
0,720,3.4,3
0,640,3.3,2
1,660,3.6,3
1,400,3.15,2
1,680,3.98,2
0,220,2.83,3
0,580,3.46,4
1,540,3.17,1
0,580,3.51,2
0,540,3.13,2
0,440,2.98,3
0,560,4.0,3
0,660,3.67,2
0,660,3.77,3
1,520,3.65,4
0,540,3.46,4
1,300,2.84,2
1,340,3.0,2
1,780,3.63,4
1,480,3.71,4
0,540,3.28,1
0,460,3.14,3
0,460,3.58,2
0,500,3.01,4
0,420,2.69,2
0,520,2.7,3
0,680,3.9,1
0,680,3.31,2
1,560,3.48,2
0,580,3.34,2
0,500,2.93,4
0,740,4.0,3
0,660,3.59,3
0,420,2.96,1
0,560,3.43,3
1,460,3.64,3
1,620,3.71,1
0,520,3.15,3
0,620,3.09,4
0,540,3.2,1
1,660,3.47,3
0,500,3.23,4
1,560,2.65,3
0,500,3.95,4
0,580,3.06,2
0,520,3.35,3
0,500,3.03,3
0,600,3.35,2
0,580,3.8,2
0,400,3.36,2
0,620,2.85,2
1,780,4.0,2
0,620,3.43,3
1,580,3.12,3
0,700,3.52,2
1,540,3.78,2
1,760,2.81,1
0,700,3.27,2
0,720,3.31,1
1,560,3.69,3
0,720,3.94,3
1,520,4.0,1
1,540,3.49,1
0,680,3.14,2
0,460,3.44,2
1,560,3.36,1
0,480,2.78,3
0,460,2.93,3
0,620,3.63,3
0,580,4.0,1
0,800,3.89,2
1,540,3.77,2
1,680,3.76,3
1,680,2.42,1
1,620,3.37,1
0,560,3.78,2
0,560,3.49,4
0,620,3.63,2
1,800,4.0,2
0,640,3.12,3
0,540,2.7,2
0,700,3.65,2
1,540,3.49,2
0,540,3.51,2
0,660,4.0,1
1,480,2.62,2
0,420,3.02,1
1,740,3.86,2
0,580,3.36,2
0,640,3.17,2
0,640,3.51,2
1,800,3.05,2
1,660,3.88,2
1,600,3.38,3
1,620,3.75,2
1,460,3.99,3
0,620,4.0,2
0,560,3.04,3
0,460,2.63,2
0,700,3.65,2
0,600,3.89,3