题目链接。
分析:
本题就是有一条边的权值可以减半情况下的求两点间的最短路。
一开始我想的是先求出不考虑减半情况下的最短路,然后将最短路中的最大权值减半。这样得到的结果是不对的。如下图:
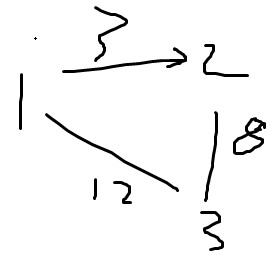
如果先找不减半最短路1->2->3。总花费为11。将最大的8除以2,所得结果为7。而从1到3将边权减半得到的是6.所以符合题意的最短路应该为1->3。所以先不考虑减半求最短路的想法是走不通的。
如此的话,本题可以用两次spfa分别求两个点到所有点的最短路,然后分别枚举每一条边权值减半的情况。
AC(未优化)代码如下:
 View Code
View Code
#include <cstdio> #include <cstring> #include <queue> using namespace std; const int INF = (1<<28); #define MAXN 1010 #define MAXM 50010 struct node{ int u, v, w; int next; }edge[MAXM*2]; queue<int> q; int head[MAXN], n, m, top, vis[MAXN], d1[MAXN], d2[MAXN]; void Init(){ int i; top = 0; for(i=1; i<=n; i++){ head[i] = -1; } } void add(int u, int v, int w){ edge[top].u = u; edge[top].v = v; edge[top].w = w; edge[top].next = head[u]; head[u] = top++; } void spfa(int v0, int *d){ int u, i; for(i=1; i<=n; i++) {d[i] = INF; vis[i] = 0;} d[v0] = 0; vis[v0] = 1; q.push(v0); while(!q.empty()){ u = q.front(); q.pop(); vis[u] = 0; for(i=head[u]; i != -1; i = edge[i].next){ int v = edge[i].v, w = edge[i].w; if(d[u]+w < d[v]){ d[v] = d[u]+w; if(!vis[v]){ vis[v] = 1; q.push(v); } } } } } int _min(int x, int y){ return x < y ? x : y; } int main(){ int i, u, v, w, s, e, min_num; while(scanf("%d %d", &n, &m) == 2){ Init(); min_num = INF; for(i=0; i<m; i++){ scanf("%d %d %d", &u, &v, &w); add(u, v, w); add(v, u, w); } scanf("%d %d", &s, &e); spfa(s, d1); spfa(e, d2); if(d1[e] >= INF || d2[s] >= INF) {printf("No solution\n"); continue;} for(i=0; i<top; i++){ min_num = _min(min_num, d1[edge[i].u]+edge[i].w/2+d2[edge[i].v]); } printf("%d\n", min_num); } return 0; }
学了一下slf优化,但对本题而言,优化后和未优化跑时是差不多的。
AC(slf优化)代码如下:
 View Code
View Code
1 #include <cstdio> 2 #include <cstring> 3 #include <deque> 4 5 using namespace std; 6 7 const int INF = (1<<28); 8 9 #define MAXN 1010 10 #define MAXM 50010 11 12 struct node{ 13 int u, v, w; 14 int next; 15 }edge[MAXM*2]; 16 17 deque<int> q; 18 int head[MAXN], n, m, top, vis[MAXN], d1[MAXN], d2[MAXN]; 19 20 void Init(){ 21 int i; 22 top = 0; 23 for(i=1; i<=n; i++){ 24 head[i] = -1; 25 } 26 } 27 28 void add(int u, int v, int w){ 29 edge[top].u = u; 30 edge[top].v = v; 31 edge[top].w = w; 32 edge[top].next = head[u]; 33 head[u] = top++; 34 } 35 36 void spfa(int v0, int *d){ 37 int u, i; 38 39 for(i=1; i<=n; i++) {d[i] = INF; vis[i] = 0;} 40 41 d[v0] = 0; 42 vis[v0] = 1; 43 q.push_back(v0); 44 45 while(!q.empty()){ 46 u = q.front(); q.pop_front(); 47 vis[u] = 0; 48 for(i=head[u]; i != -1; i = edge[i].next){ 49 int v = edge[i].v, w = edge[i].w; 50 if(d[u]+w < d[v]){ 51 d[v] = d[u]+w; 52 if(!vis[v]){ 53 vis[v] = 1; 54 if(!q.empty()){ 55 if(d[v]>d[q.front()]) q.push_back(v); 56 else q.push_front(v); 57 } 58 else q.push_back(v); 59 } 60 } 61 } 62 } 63 } 64 65 int _min(int x, int y){ 66 return x < y ? x : y; 67 } 68 69 int main(){ 70 int i, u, v, w, s, e, min_num; 71 72 while(scanf("%d %d", &n, &m) == 2){ 73 Init(); 74 min_num = INF; 75 for(i=0; i<m; i++){ 76 scanf("%d %d %d", &u, &v, &w); 77 add(u, v, w); 78 add(v, u, w); 79 } 80 scanf("%d %d", &s, &e); 81 spfa(s, d1); spfa(e, d2); 82 83 if(d1[e] >= INF || d2[s] >= INF) {printf("No solution\n"); continue;} 84 85 for(i=0; i<top; i++){ 86 min_num = _min(min_num, d1[edge[i].u]+edge[i].w/2+d2[edge[i].v]); 87 } 88 89 printf("%d\n", min_num); 90 } 91 92 return 0; 93 }
