HDU2602Bone Collector(DP,0/1背包)

题目连接

解题报告：

结合算法竞赛入门经典（刘汝佳）， 算法设计与分析（郑宗汉，郑晓明）花了一天才算弄懂0/1背包思想，当然仅仅是入门而已

给定一个载重量为M, n个重量为wi,价值为pi的物体,1<=i<=n, 每个物品xi都有两种状态，即放入(0)和不放入(1)，即xi=0或xi=1

使得价值最大。

   

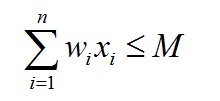
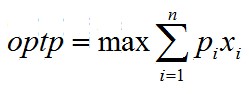
状态转移方程为f[i][j]=max{f[i-1][j],f[i-1][v-w[i]]+p[i]}

一篇博客介绍的相当不错。

（里面介绍的思路（设的变量名称可能会不一样）：

问题的特点是：每种物品一件，可以选择放1或不放0。

用子问题定义状态：即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是：

f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}

这个方程非常重要，据说基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以详细的查了一下这个方程的含义：“将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”，价值为f[i-1][v]；如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。

在有的地方看到的背包问题题目中，有两种不太相同的问法。有的题目要求“恰好装满背包”时的最优解，有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。

如果是第一种问法，要求恰好装满背包，那么在初始化时除了f[0]为0其它f[1..V]均设为-∞，这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。

如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将f[0..V]全部设为0。

为什么呢？可以这样理解：初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可能被价值为0的nothing“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，它们的值就都应该是-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。）

另外， 我在提交的过程中WA了很多次。

原因是

第一种方法中的for(j=0; j<=v; j++)写成了for(j=1; j<=v; j++)

或者是第二种方法中的for(j=v; j>=0; j--)写成了for(j=v; j>=1; j--)

这是不对的。。为什么呢。。因为可能会有体积为0，但却有价值的骨头。。。

总之对于该题的代码如下：

#include <stdio.h>

#define MAXN 1002

int dp[MAXN][MAXN], w[MAXN], p[MAXN];

int _max(int a, int b){
    return a > b ? a : b;
}

int main(){

    int n, v, T, i, j;
    scanf("%d", &T);
    while(T--){
        scanf("%d %d", &n, &v);
        for(i=1; i<=n; i++){
            scanf("%d", &w[i]);
        }
        for(i=1; i<=n; i++){
            scanf("%d", &p[i]);
        }
        for(i=0; i<=n; i++) dp[i][0] = 0;
        for(i=0; i<=v; i++) dp[0][i] = 0;
        
        for(i=1; i<=n; i++){
            for(j=0; j<=v; j++){
                dp[i][j] = dp[i-1][j];
                if(j>=p[i]) dp[i][j] = _max(dp[i-1][j], dp[i-1][j-p[i]]+w[i]);
            }
        }
        printf("%d\n", dp[n][v]);
    }

    return 0;
}

将数组变为一维的代码：

#include <stdio.h>
#include <string.h>

#define MAXN 1002

int max_num(int a, int b){
    return a > b? a : b;
}

int dp[MAXN], w[MAXN], p[MAXN];

int main(){

    int n, v, T, i, j;
    scanf("%d", &T);
    while(T--){
        scanf("%d %d", &n, &v);
        for(i=1; i<=n; i++){
            scanf("%d", &w[i]);
        }
        for(i=1; i<=n; i++){
            scanf("%d", &p[i]);
        }
        for(i=0; i<=v; i++){
            dp[i] = 0;
        }
        for(i=1; i<=n; i++){
            for(j=v; j>=0; j--){
                if(j>=p[i]) dp[j] = max_num(dp[j], dp[j-p[i]]+w[i]);
            }
        }
        printf("%d\n", dp[v]);
    }

    return 0;
}