记intel杯比赛中各种bug与debug【其五】：朴素贝叶斯分类器的实现和针对性的优化

咱这个项目最主要的就是这个了
贝叶斯分类器用于做可以统计概率的二元分类
典型的例子就是垃圾邮件过滤

理论基础

对于贝叶斯算法，这里附上两个链接，便于理解：
朴素贝叶斯分类器的应用-阮一峰的网络日志
基于朴素贝叶斯到中文垃圾邮件分类器
朴素贝叶斯分类器和一般的贝叶斯分类器有什么区别？-知乎

这里我们用朴素贝叶斯分类，假设所有特征都彼此独立，贝叶斯公式是这样

[P(A|B)=frac{P(B|A)P(A)}{P(B)}=frac{P(B|A)P(A)}{P(B|A)+P(B|ar{A})} ]

现在我们收到一封邮件，假设T为此邮件为垃圾邮件，Wn为第N个词的存在
$ P(T|W_{n}) $的意思是在第n个词的存在下，这封邮件为垃圾邮件的概率
那么垃圾邮件和正常邮件的概率比就是这样的

[frac{P(T)}{P(ar{T})}=frac{P_{prior}(T)}{P_{prior}(ar{T})} prod{frac{P(W_{n}|T)}{P(W_{n}|ar{T})}} ]

代码实现

class BeyasFilter:
	# 0-ham 1-spam
	def __init__(self):
		self.count=[0, 0]
		self.prior=1
		self.freq={}

	def train(self, words, label):
		# label: 0-ham 1-spam
		for word in words:
			self.count[label]+=1
			if word not in self.freq:
				self.freq[word]=[0, 0]
			self.freq[word][label]+=1

	 def isspam(self, content):
		pred=self.prior
		words=self.segment(content)
		for word in words:
			if self.freq.get(word) and self.freq[word][1]!=0 and self.freq[word][0]!=0:
				pred*=(self.freq[word][1]*self.count[0])/(self.freq[word][0]*self.count[1])
		return True if pred>1 else False

做一个小小的优化

• 在贝叶斯决策时，若发现某一个词汇并没有在训练字典中出现，我们使用拉普拉斯平滑(Laplace Smoothing)对其进行处理。
  原理即是设定一个很小的值作为其后验概率。这样做保证在处理新词时，不会让后验概率乘零，也不会让后验概率乘壹而放过这个信息。及决策变为：
  

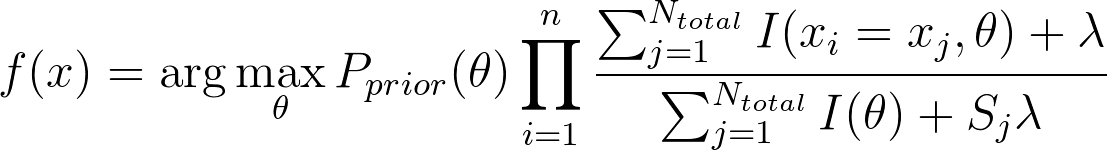
• 在处理较短的句子时，贝叶斯分类器很可能造成误判，比如消息“欢迎”。“欢迎”经常出现在重要消息中。但是这样一个短句独立的出现时，我们一般认为其是垃圾信息（因为不是重要信息）。通过贝叶斯决策理论发现我们难以处理这样的情况，所以我们对此作出优化。我们认为先验概率应包含句子长度的概率密度，最终优化效果令人满意。通过核概率密度估计，对句子长度做出统计，并在计算后验概率之后乘以这个调节函数，即可对短句作出优化。
  具体的先验概率函数设计是这样的：
  a. 首先对句子长度做出统计、平滑，得到下表。其中橙线为垃圾信息句子长度的概率密度，蓝线为重要信息句子长度的概率密度：
  
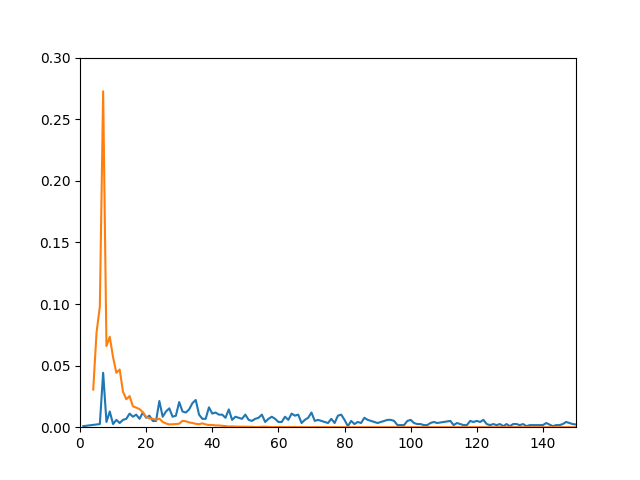
  b. 结合图表，我们发现句子长度在垃圾信息和重要信息下的有较大分布差异
  c. 设计一个函数，这个函数返回当前句子长度在垃圾信息和在重要信息中的概率比
  d. 最终设计出函数：
  

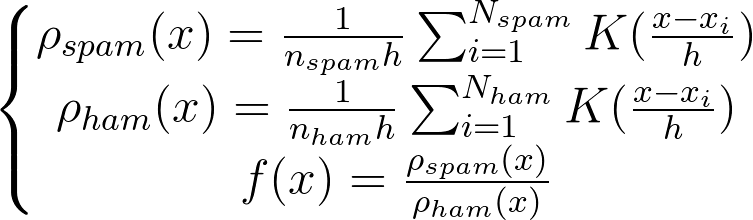
2018-02-28 Update: 修改一个关于先验概率的默认取值的错误
2018-08-02 Update: 写的什么垃圾，发现忘了更新这篇。优化部分用文档重写了