LeetCode 树 230. 二叉搜索树中第K小的元素（二叉搜索树 中序遍历 剪枝）

 相对来说比较简单的一道题目。

第一反应是，搞个数组把整个搜索树搞个排序，然后就完事了。

自然想到，搜索二叉树的中序遍历即是一个升序排列的方式。因为中序排列就是一个先左子树，再root，再右子树的遍历方式。

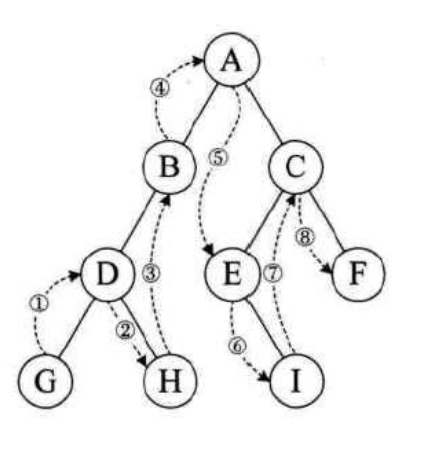
 自然的想到使用递归实现中序遍历：

• 递归函数的作用：将整棵树的节点按中序放到一个ArrayList中
• 递归函数结束条件：节点为null
• 递归函数的逻辑关系：F(root)=F(root.left)+root.val+F(root.right)

class Solution {
  public ArrayList<Integer> inorder(TreeNode root, ArrayList<Integer> arr) {
    if (root == null) return arr;
    inorder(root.left, arr);
    arr.add(root.val);
    inorder(root.right, arr);
    return arr;
  }

  public int kthSmallest(TreeNode root, int k) {
    ArrayList<Integer> nums = inorder(root, new ArrayList<Integer>());
    return nums.get(k - 1);
  }
}

显然看出，时间复杂度和空间复杂度都是On

但是我们可以构造一个大小为k的栈，只需要找到第k小的就行了

或者可以搞一个二叉搜索树的剪枝

class Solution {
    int n = 0;
    int ans = 0;

    public int kthSmallest(TreeNode root, int k) {
        search(root, k);
        return ans;
    }

    private void search(TreeNode node, int k) {
        
        if(node!=null)
        {
            search(node.left, k);
            n++;
            if (n == k) {
                ans = node.val;
            } else if (n > k) {
                return;//剪枝
            }
            search(node.right, k);
        }
       

    }
}