Dijkstra在正权图上运行速度很快,但是它不能解决有负权的最短路,如下图:
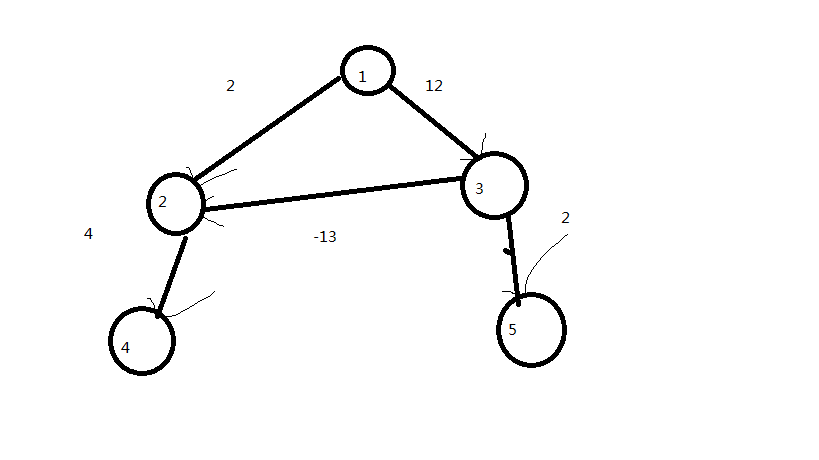
Dijkstra运行的结果是(以1为原点):0 2 12 6 14;
但手算的结果,dist[4]的结果显然是5,为什么会出现这种情况呢?原因很显然,Dijkstra认为,从一个更长的边过来不会比一个更短的边过来更短(读起来很绕口,但请读者好好理解这句话!)但是由于出现了负权边,可以“救回来”,就像松弛2号节点一样。
Bellman_Ford:
知道了Dijkstra为什么不能做负权图之后,我们来看看Bellman-ford算法。它的基本思想是:图的最短路,既不会包含正环(可以不走),更不能有负环(否则一直走就可以无限小),因此最多经过n-1条边(每个节点都经过一次),bellman-ford实际上是枚举距离源点多少条边,尝试对每条边松弛的过程。请读者联系上图,自行推导一下Bellman_ford的运行过程
样例如下:
5 5
1 2 2
1 3 12
3 2 -13
2 4 4
3 5 2
朴素Bellman_Ford算法的时间复杂度是O(NM);程序如下:

1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #include<cstring> 5 using namespace std; 6 int n,m,s,dist[100001],v[200005],w[200005],u[200005],cnt,x,y,z; 7 void bellman_ford(int s) 8 { 9 memset(dist,20,sizeof(dist)); 10 dist[s]=0; 11 for(int i=1;i<=n-1;i++) 12 { 13 for(int j=1;j<=m;j++) 14 { 15 dist[v[j]]=min(dist[v[j]],dist[u[j]]+w[j]); 16 } 17 } 18 } 19 int main() 20 { 21 scanf("%d %d",&n,&m); 22 for(int i=1;i<=m;i++) 23 { 24 scanf("%d %d %d",&u[i],&v[i],&w[i]); 25 } 26 bellman_ford(1); 27 for(int i=1;i<=n;i++) 28 { 29 cout<<dist[i]<<" "; 30 } 31 return 0; 32 }
SPFA:
SPFA是对Bellman_Ford算法的优化,它采用队列保存即将松弛其他点的节点,每次选与队首相连的点进行松弛,可以使用链式前向星(邻接表)实现,避免了Bellman_Ford算法许多无效的松弛操作,平均复杂度O(KM),K为平均松弛次数,也有可能被网格图卡回O(NM),是不稳定的算法。程序如下:

1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #include<cstring> 5 using namespace std; 6 int n,m,s,dist[100001],v[200005],w[200005],nxt[200005],head[200005],cnt,x,y,z; 7 bool vis[100001]; 8 void add(int a,int b,int c) 9 { 10 v[++cnt]=b; 11 w[cnt]=c; 12 nxt[cnt]=head[a]; 13 head[a]=cnt; 14 } 15 void SPFA(int s) 16 { 17 memset(dist,20,sizeof(dist)); 18 queue<int>q; 19 dist[s]=0; 20 vis[s]=1; 21 q.push(s); 22 while(!q.empty()) 23 { 24 int c=q.front(); 25 q.pop(); 26 vis[c]=0; 27 for(int i=head[c];i;i=nxt[i]) 28 { 29 int y=v[i]; 30 if(dist[y]>=dist[c]+w[i]) 31 { 32 dist[y]=dist[c]+w[i]; 33 if(!vis[y]) 34 { 35 q.push(y); 36 vis[y]=1; 37 } 38 } 39 } 40 } 41 } 42 int main() 43 { 44 scanf("%d %d",&n,&m); 45 for(int i=1;i<=m;i++) 46 { 47 scanf("%d%d%d",&x,&y,&z); 48 add(x,y,z); 49 } 50 SPFA(1); 51 for(int i=1;i<=n;i++) 52 { 53 cout<<dist[i]<<" "; 54 } 55 return 0; 56 }
