题目描述
无向连通图G有n个点,n-1 条边。点从1到n依次编号,编号为i的点的权值为W_i
,每条边的长度均为 1。图上两点(u,v) 的距离定义为 u 点到 v 点的最短距离。对于图 G 上的点对 (u,v),若它们的距离为 2,则它们之间会产生Wv*Wu的联合权值。
请问图 G上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入输出格式
输入格式:
第一行包含 1个整数 n。
接下来 n-1 行,每行包含 2个用空格隔开的正整数 u,v表示编号为 u 和编号为 v 的点之间有边相连。
最后 1 行,包含 n 个正整数,每两个正整数之间用一个空格隔开,其中第 i 个整数表示图 G 上编号为 i 的点的权值为 W_i。
输出格式:
输出共 1 行,包含 2 个整数,之间用一个空格隔开,依次为图 G 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对10007取余。
输入输出样例
输入样例#1:
5
1 2
2 3
3 4
4 5
1 5 2 3 10
输出样例#1:
20 74
说明
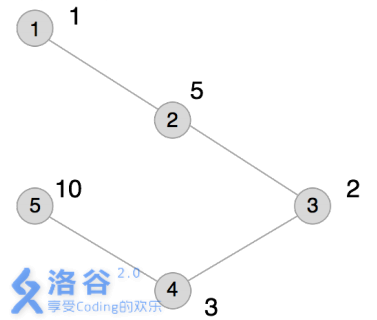
本例输入的图如上所示,距离为2 的有序点对有(1,3) 、(2,4) 、(3,1) 、 (3,5)、(4,2) 、(5,3)。
其联合权值分别为2 、15、2 、20、15、20。其中最大的是20,总和为74。
【数据说明】
对于30%的数据,1<n≤100;
对于60%的数据,1<n≤2000;
对于100%的数据,1<n200000,0<Wi≤10000。
保证一定存在可产生联合权值的有序点对。
解析:
5年前的D1T2我调了3天没调出来,orz了一堆大佬才懂???
根据题目给的条件可知这是一颗树,目标就是说去求所有距离为2的点权值之积的和与最大值,第一想法是去枚举每个节点,找出所有与它距离为2的点,但是很明显会超时,只能得到70分,究其原因则是因为无向边要计算两遍,顺着这个思路走,会想到去组合边,之后整体×2即可,于是想到要去枚举中间的转折点(其实一开始就应该想到,因为故意要求距离为2的点),这个过程实际上还是一个乘法分配律的应用,当前的点要和之前的点一个一个乘,不必去枚举其它点,只需记录它们的和,有点类似于前缀和的思想,但实际上是一个乘法分配律的应用。而以当前节点作为中转点的最大联合权值,肯定是最大数乘上次大数,在这里不用记录次大数,只需线性扫一遍打一遍擂台即可
最后上AC代码

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 long long n,x,y,v[500001],head[500001],nxt[500001],cnt,w[200001]; 6 long long sum,maxx; 7 void add(int a,int b)//链式前向星存边,效率高,在图论中有很重要的作用 8 { 9 v[++cnt]=b;//v[cnt]表示编号为cnt的边的终点 10 nxt[cnt]=head[a];//nxt[cnt]表示第cnt条边下一条边是head[a] 11 head[a]=cnt;//插入链表头部 12 } 13 int main() 14 { 15 scanf("%lld",&n); 16 for(int i=1;i<n;i++) 17 { 18 scanf("%lld%lld",&x,&y); 19 add(x,y);//无向边存两次 20 add(y,x); 21 } 22 for(int i=1;i<=n;i++)scanf("%lld",&w[i]); 23 for(int i=1;i<=n;i++) 24 { 25 long long fix=0,maxn=0; 26 for(int j=head[i];j;j=nxt[j]) 27 { 28 sum+=(fix*w[v[j]])%10007;//和之前的数每个相乘再相加,只需加他们的和就好了。 29 fix+=w[v[j]];//根据乘法分配律,打前缀和 30 maxx=max(maxx,maxn*w[v[j]]);//打擂台取最大值 31 maxn=max(maxn,w[v[j]]); 32 } 33 } 34 cout<<maxx<<" "<<sum*2%10007; 35 return 0; 36 }
