一.HashMap底层源码剖析
1.介绍HashMap底层用到的数据结构
数组:数组的每一项都是一个链表,其实就是数组和链表的结合体

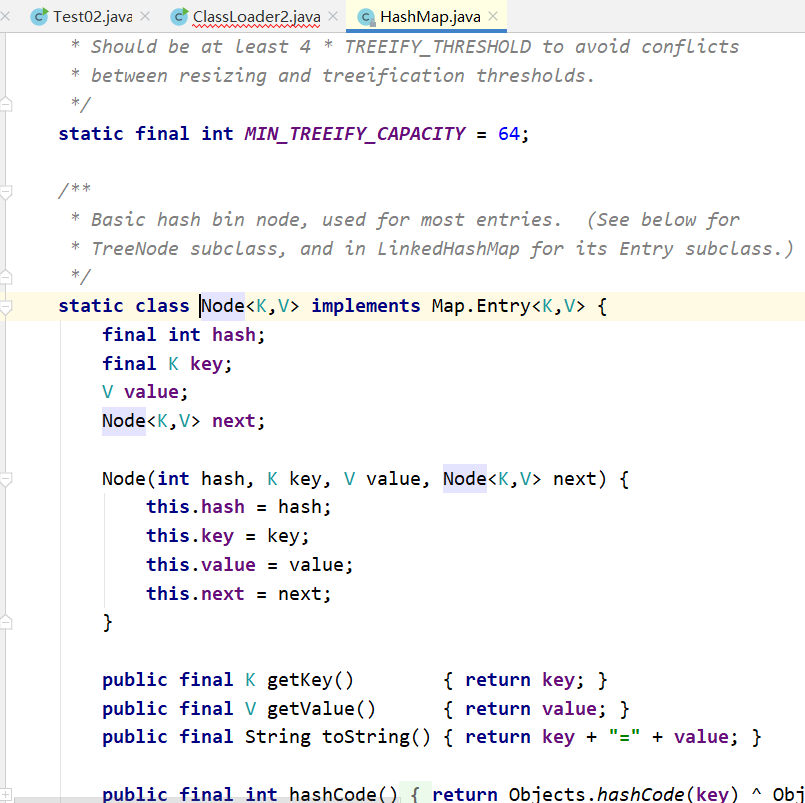
单向链表:当发生Hash碰撞时,首先会找到数组对应位置,然后1.8采用尾插入法(1.7采用头插入法)

形成一个单向链表结构
jdk1.8 后 红黑树:当数组中每项的链表长度大于8时,会转换为红黑树,效率更快
能够解释一下什么是Hash碰撞?解决办法有哪一些
不同的key可能会产生相同的Hash值
解决Hash碰撞的办法:链表法(参考上图)
再哈希法HashMap当中采用链表发,在ConcurrentHashMap当中采用再哈希法
2.为什么采用红黑树,比如二叉查找树,并且为什么临界值为8
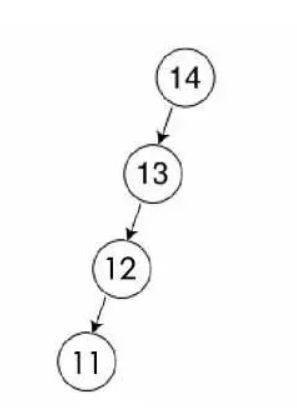
红黑树是一种平衡树,他复杂的定义和规则都是为了保证树的平衡性。如果树不保证他的平衡性就是下图:很显然这就变成一个链表了。二叉查找树在特殊情况下也会变为线性结构,和原来链表有共同的问题,节点太深,查找性能慢
红黑树是平衡二叉树的一种,插入新的数据都会通过左旋,右旋,变色等操作来保持平衡
保证平衡性的最大的目的就是降低树的高度,因为树的查找性能取决于树的高度。所以树的高度越低搜索的效率越高!
如下图:
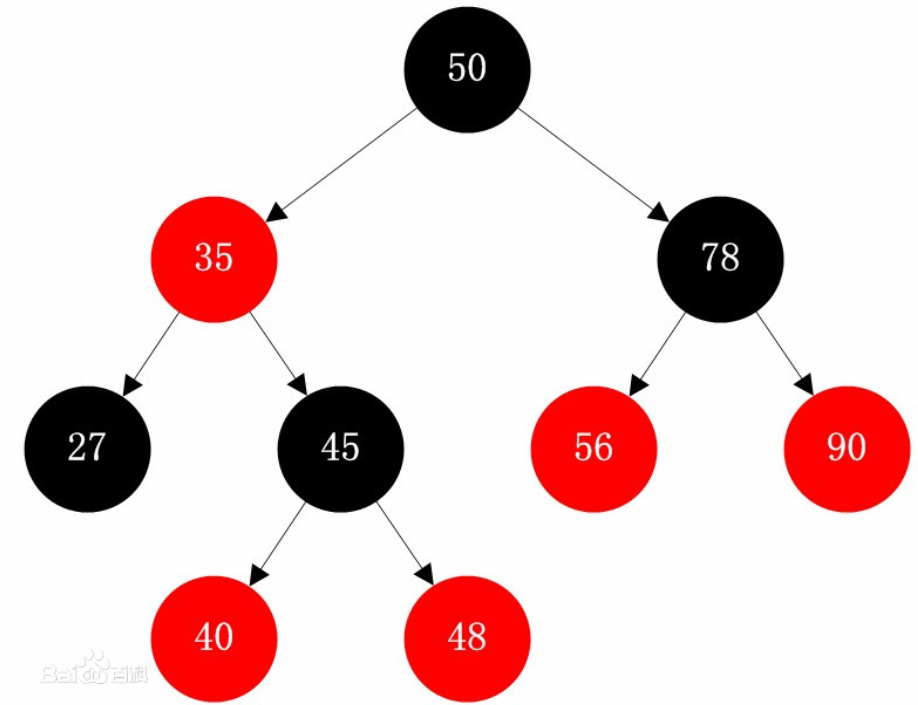
当数据较少时,采用链表要比红黑树效率高,因为平衡二叉树保持平衡需要耗费资源,那么前期数据较少时采用链表,
当数据到达一定的界限后,再采用红黑树,可以加快数据查询速度,官方测试8为性能最优~
3.put和get底层源码的核心流程
put方法核心:
public V put(K key, V value) { //计算key的Hash值,然后将Hash值以及key值本身和Value传递到putval方法当中 return putVal(hash(key), key, value, false, true); } final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0) //判断当前数组是否为空,如果为空要进行第一次扩容 n = (tab = resize()).length; //扩容后将扩容大小交给N if ((p = tab[i = (n - 1) & hash]) == null) //判断获取当前数组位置是否存在数据,如果为空则直接插入,否则需要代表当前位置不是空的,不是空的需要判断 tab[i] = newNode(hash, key, value, null); //如果为空则创建一个新的节点添加到该位置 else { Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) //判断Hash值和Key值是否相同,如果相同则需要Value覆盖 e = p; else if (p instanceof TreeNode) //判断当前数组中存放的节点是否是树节点 e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); //则添加树节点即可 else { for (int binCount = 0; ; ++binCount) { //循环遍历链表 if ((e = p.next) == null) { //判断当前数组该位置的值得下一个元素是否为空,如果为空则追加到当前元素后边 p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st //添加完毕后判断当前链表节点有多少个,如果节点大于等于8则转换为红黑树 treeifyBin(tab, hash); //treeifyBin判断当前数组是否为空,或者长度是否小于64,如果为空或者小于64 //则先扩容 break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) //再次进行Key的重复判断 break; p = e; } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) //判断当前数组元素个数和阀值进行比较,如果数量大于阀值则需要扩容 resize(); //默认情况下,第一次添加数据的时候,先会进行一次扩容后再添加数据 afterNodeInsertion(evict); //后续都是先添加数据再扩容 return null; }
扩容: 默认情况下,数组大小为16,当数组元素 超过大小*负载因子(0.75),如果超过12个元素,则调用resize进行扩容,
扩容原来大小的2倍并且重新计算数组中元素的位置,所以比较耗费性能,一般创建集合尽量预知大小,避免多次扩容
get方法核心逻辑:
final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { //判断数组以及数组对应位置数组元素是否为空 if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) //用get传递过来的Key值和对应位置第一个元素进行比较,如果相等直接返回,如果不等则进行查找 return first; if ((e = first.next) != null) { //判断第一个元素的下一个元素是否为空,如果不为空 if (first instanceof TreeNode) //如果不为空判断当前节点是否为树节点 return ((TreeNode<K,V>)first).getTreeNode(hash, key); //如果是树节点,直接通过getTreeNode拿到该节点返回 do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) //循环一一对比 return e; } while ((e = e.next) != null); } } return null; }
二.ConcurrentHashMap底层实现
1.ConcurrentHashMap和HashTable之间
ConcurrentHashMap性能高于HashTable,都能够完成线程安全操作,
Hashtable中线程安全使用synchronized同步方法进行加锁操作,如果当前一个线程正在访问该集合,其他线程是无
法进行访问的,需要进行等待.
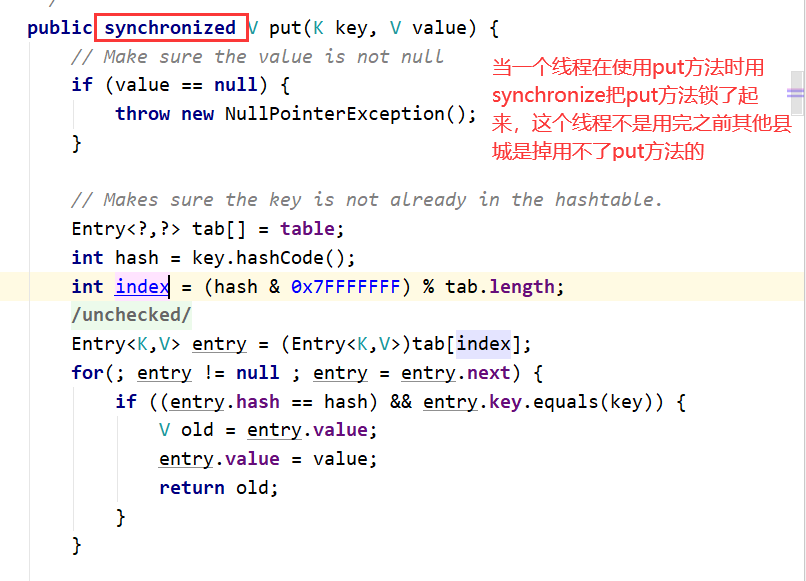
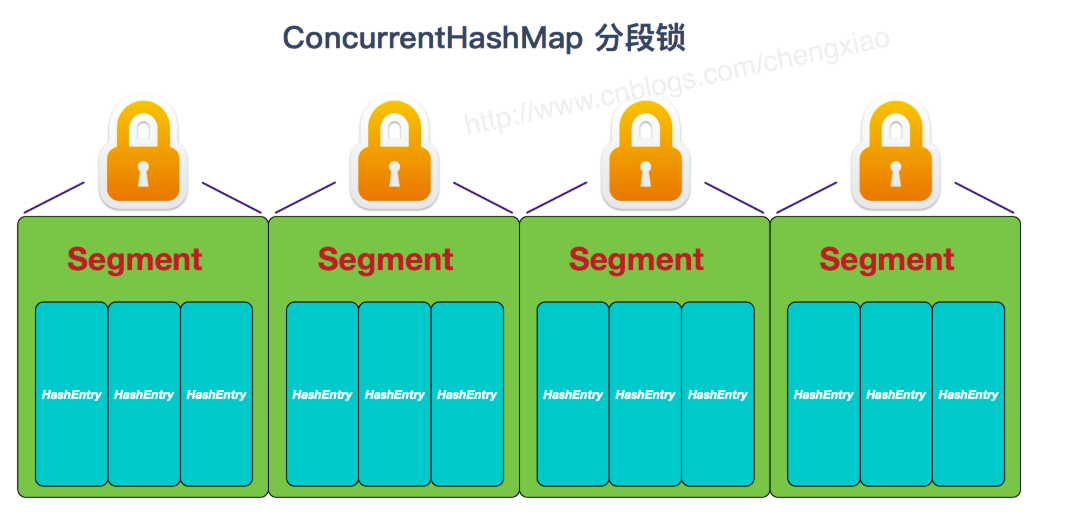
反之ConcurrentHashMap当中采用分段锁机制
JDK1.7和JDK1.8底层实现的区别
JDK1.8版本之前,ConcurrentHashMap使用分段锁技术,将数据分成一段一段的进行村粗,
每一个数据段配置一把锁Segment(继承ReentrantLock)
底层采用:Segment+HashEntry当数据添加时,根据key值找到Segment对应的数据段,然后匹配数据块,
采用链表方式进行存储
1.8版本之后,ConcurrentHashMap取消了Segment分段所的机制,底层采用Node数组+链表+红黑树,
从而实现一段数据进行加锁,减少了并发,CAS(读)+synchronized(写)
当数据添加时,根据key值找到对应数组的Node,中间采用CAS和synchronized进行数据操作
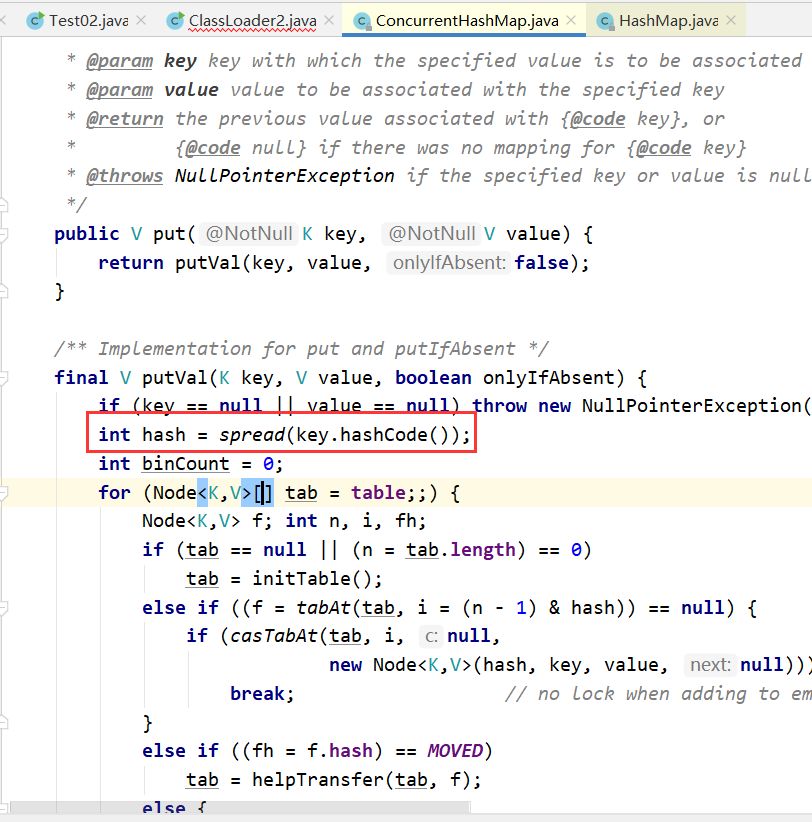
2. ConcurrentHashMap底层put方法实现的核心逻辑
public V put(K key, V value) { return putVal(key, value, false); } /** * Implementation for put and putIfAbsent */ final V putVal(K key, V value, boolean onlyIfAbsent) { if (key == null || value == null) throw new NullPointerException(); //判断key和value是否为空,如果为空则报异常 int hash = spread(key.hashCode()); /重新计算key的hash值,有效减少Hash值冲突 int binCount = 0; for (Node<K, V>[] tab = table; ; ) {//遍历当前数组当中所有的数据 Node<K, V> f; int n, i, fh; if (tab == null || (n = tab.length) == 0) //判断数组是否为空 tab = initTable(); //如果为空要进行数组的初始化操作 else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) { //根据key的Hash值找到位置,如果该位置没有元素 if (casTabAt(tab, i, null, new Node<K, V>(hash, key, value, null)))//获取到空的元素,然后重新创建一个新的Node放进去 break; // no lock when adding to empty bin } else if ((fh = f.hash) == MOVED) //判断当前数组元素状态是否需要扩容 tab = helpTransfer(tab, f); else { V oldVal = null; synchronized (f) { //加锁 if (tabAt(tab, i) == f) { if (fh >= 0) { binCount = 1; for (Node<K, V> e = f; ; ++binCount) { K ek; if (e.hash == hash && //判断添加的key和原有key进行Hash值判断以及key值判断,如果相等则覆盖 ((ek = e.key) == key || (ek != null && key.equals(ek)))) { oldVal = e.val; if (!onlyIfAbsent) e.val = value; break; } Node<K, V> pred = e; if ((e = e.next) == null) {//判断当前节点的下一个节点是否为空,如果为空则添加到下一个节点当中 pred.next = new Node<K, V>(hash, key, value, null); break; } } } else if (f instanceof TreeBin) { //判断当前节点是否为红黑树 Node<K, V> p; binCount = 2; if ((p = ((TreeBin<K, V>) f).putTreeVal(hash, key, value)) != null) { //如果为红黑树则创建一个树节点 oldVal = p.val; if (!onlyIfAbsent) p.val = value; } } } } if (binCount != 0) { if (binCount >= TREEIFY_THRESHOLD) //根据当前循环次数判断链表中存在多少个数据,如果数据阀值大于等于8 //则进行红黑树转换 treeifyBin(tab, i); if (oldVal != null) return oldVal; break; } } } addCount(1L, binCount);//判断是否需要扩容 return null; }