背景重述
本文是ESL: 12.3 支持向量机和核中表12.2的重现过程。具体问题如下:
在两个类别中产生100个观测值。第一类有4个标准正态独立特征(X_1,X_2,X_3,X_4)。第二类也有四个标准正态独立特征,但是条件为(9le sum X_j^2le 16)。这是个相对简单的问题。同时考虑第二个更难的问题,用6个标准高斯噪声特征作为增广特征。
生成数据
## #####################################
## generate dataset
##
## `No Noise Features`: num_noise = 0
## `Six Noise Features`: num_noise = 6
## #####################################
genXY <- function(n = 100, num_noise = 0)
{
## class 1
m1 = matrix(rnorm(n*(4+num_noise)), ncol = 4 + num_noise)
## class 2
m2 = matrix(nrow = n, ncol = 4 + num_noise)
for (i in 1:n) {
while (TRUE) {
m2[i, ] = rnorm(4 + num_noise)
tmp = sum(m2[i, 1:4]^2)
if(tmp >= 9 & tmp <= 16)
break
}
}
X = rbind(m1, m2)
Y = rep(c(1, 2), each = n)
return(data.frame(X = X, Y = as.factor(Y)))
}
模型训练
- SVM直接调用
e1071包中的svm函数 - BRUTO和MARS都是调用
mda包,且由于两者都是用于回归,所以转换为分类时,是比较拟合值与类别标签的距离,划分到越靠近的那一类 - 原书中提到实验中MARS不限定阶数,但实际编程时,设置阶数为10
交叉验证选择合适的(C)
我分两步进行选择:
- 粗选:在较大范围内寻找最优的(C)
- 细分:在上一步选取的最优值附近进行细分
注意避免最优值取在边界值。以SVM/poly5为例进行说明,其他类似
## SVM/poly5
set.seed(123)
poly5 = tune.svm(Y~., data = dat, kernel = "polynomial", degree = 5, cost = 2^(-4:8))
summary(poly5)
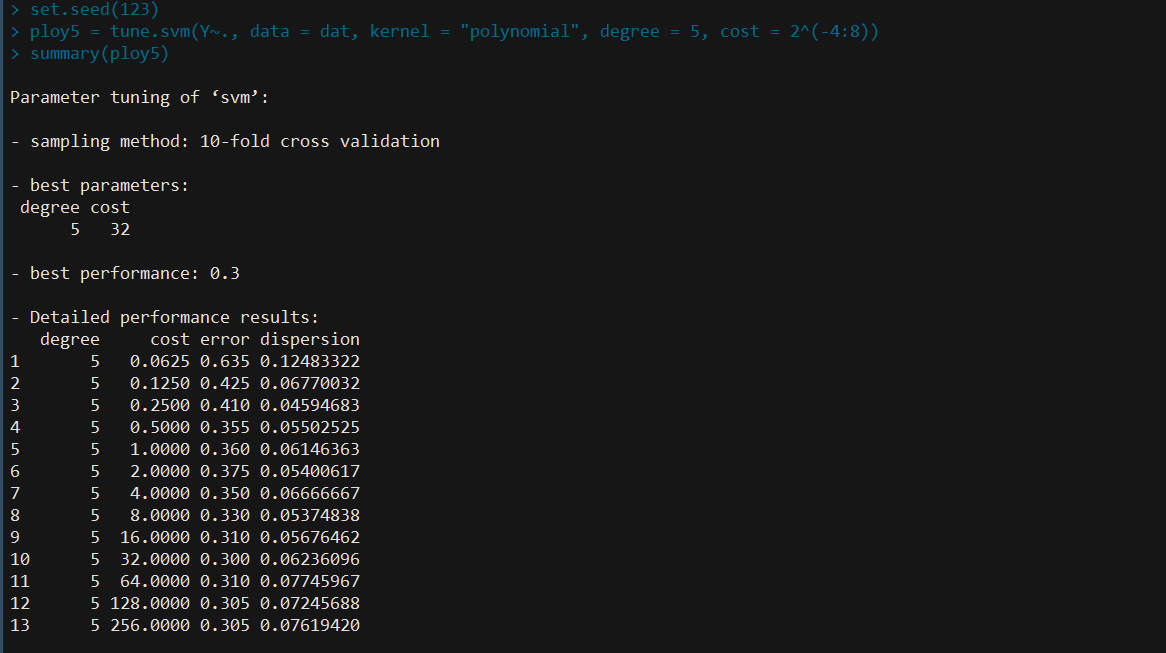
此时选取的最优(C)为32,进一步细化
set.seed(1234)
poly5 = tune.svm(Y~., data = dat, kernel = "polynomial", degree = 5, cost = seq(16, 64, by = 2))
summary(poly5)

所以(C)取28。
类似地,得到其它方法的最优(C),比如某次实验结果如下:
| Method | best cost |
|---|---|
| SV Classifier | 2.6 |
| SVM/poly 2 | 1 |
| SVM/poly 5 | 28 |
| SVM/poly 10 | 0.5 |
当然,实际中我们并不需要重新设置参数来训练模型,因为tune.svm()的返回结果就包含了最优模型,直接调用,比如poly5$best.model
计算测试误差
predict.mars2 <- function(model, newdata)
{
pred = predict(model, newdata)
ifelse(pred < 1.5, 1, 2)
}
calcErr <- function(model, n = 1000, nrep = 50, num_noise = 0, method = "SVM")
{
err = sapply(1:nrep, function(i){
dat = genXY(n, num_noise = num_noise)
datX = dat[, -ncol(dat)]
datY = dat[, ncol(dat)]
if (method == "SVM")
pred = predict(model, newdata = datX)
else if (method == "MARS")
pred = predict.mars2(model, newdata = datX)
else if (method == "BRUTO")
pred = predict.mars2(model, newdata = as.matrix(datX))
sum(pred != datY)/(2*n) # Attention!! The total number of observations is 2n, not n
})
return(list(TestErr = mean(err),
SE = sd(err)))
}
值得说明的是,对于BRUTO和MARS,因为程序是将其视为回归模型处理的,需要进一步转换为类别标签。因为程序中类别用1和2编号,所以判断拟合值是否大于1.5,大于则划为第二类,否则第一类。
结果
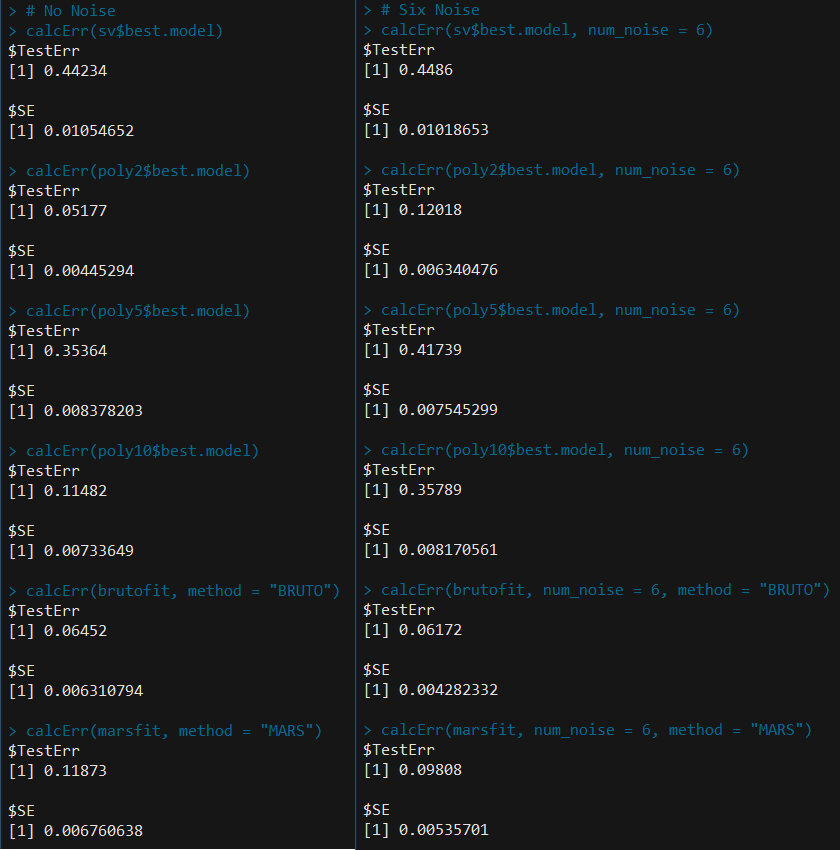
将之与表12.2进行比较,可以看出各个方法的误差率及标准差的相对大小都比较一致。
贝叶斯误差率
对于类别1,
[sum X_j^2sim chi^2(4)
]
对于类别2,
[sum X_j^2sim frac{chi^2(4)I(9lechi^2(4)le 16)}{int_9^{16} f(t)dt}
]
其中(f(t))是(chi^2(4))的密度函数。
于是贝叶斯误差率为
[frac{1}{2}int_{9}^{16}f(t)dtapprox 0.029
]
完整代码可以参见skin-of-the-orange.R
本文永久链接:模拟:Tab. 12.2